3.2 Расчет и построение естественных механических и электромеханических характеристик ад
3.2.1 Рассчитываем приведенные сопротивления
-
приведенное активное сопротивление
ротора,
Ом
– приведенное индуктивное сопротивление
ротора,
-
индуктивное сопротивление КЗ .
3.2.2 Определяем синхронную скорость
,
где fc – частота сети, р – число полюсов.
3.2.3 Определяем критический момент двигателя в двигательном режиме
3.2.4 Определяем номинальный момент двигателя
т. к. отношение Мкр/Мн = 2.9, то
3.2.5 Определяем наибольший пусковой момент двигателя
3.2.6 Определяем момент переключения
3.2.7 Определяем критическое скольжение в двигательном режиме
3.2.8 Определяем номинальное скольжение
3.2.9 Определяем скольжение по ступеням
ступень 1:
ступень 2:
3.2.10 Рассчитываем естественную механическую характеристику М=f(S) по формуле:
,
где
-
параметр, зависящий от сопротивлений
обмоток АД.
Задаемся скольжением от 0 до 1 и строим естественную характеристику М=f(S).
Данные для построения естественной механической характеристики представлены в таблице 1.
Таблица 1 – Данные для построения естественной механической характеристики М=f(S)
S |
0.001 |
0,02 |
0,1 |
0,2 |
0,3 |
0,4 |
0.6 |
0.7 |
0.8 |
0.9 |
1 |
M |
1239 |
10500 |
4473 |
2384 |
1618 |
1224 |
822,3 |
706,3 |
619 |
550,9 |
496,3 |
Естественная механическая характеристика представлена на рисунке 5.
Рисунок 5– Естественная механическая характеристикa двигателя
3.2.11 Рассчитываем электромеханические характеристики I`p=f(S), Ic=f(S)
,
,
где α = (0.11 ÷ 0.13).
Принимаю α=0.12
Задаемся скольжением от 0 до 1 и рассчитываем электромеханические характеристики. Данные расчета представлены в таблице 2.
Таблица 2 – Данные для расчета электромеханических характеристик I’p=f(S), Ic=f(S)
S |
0.001 |
0.02 |
0.1 |
0.2 |
0.3 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1 |
I`p |
119.3 |
1553 |
2266 |
2340 |
2361 |
2376 |
2380 |
2383 |
2384 |
2386 |
2387 |
Ic |
204.9 |
1763 |
2528 |
2610 |
2634 |
2651 |
2655 |
2660 |
2661 |
2663 |
2665 |
Таблица 2
Естественные электромеханические характеристики представлены на рисунках 6,7.
Рисунок 6 – Естественная электромеханическая характеристика IР́ =f(S)
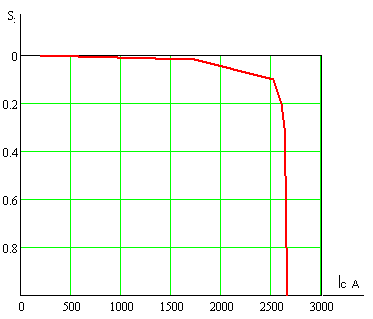
Рисунок 7 – Естественная электромеханическая характеристика IC =f(S)
3.3 Пуск и регулирование скорости ад в пределах цикла
3.3.1 Определяем добавочные сопротивления для первой ступени характеристики:
,
после приведения к общему знаменателю и некоторых преобразований, получаем:
В результате решения квадратного уравнения получаем два корня
,
.
Принимаем
- наибольшее значение из двух корней.
Определяем добавочное сопротивление для пусковой характеристики
,
получаем
,
,
где
-
приведенное добавочное сопротивление,
-
добавочное сопротивление для
характеристики первой ступени.
3.3.2 Определяем добавочное сопротивление для пусковой характеристики:
,
после приведения к общему знаменателю и некоторых преобразований, получаем
Т. к. скольжение на пусковой ступени равно 1 получаем:
В результате решения квадратного уравнения получаем два корня
,
.
Принимаем
- наибольшее значение из двух корней.
Определяем добавочное сопротивление для пусковой ступени
,
получаем
,
,
где
-
приведенное добавочное сопротивление,
-
добавочное сопротивление на пусковой
ступени.
3.3.3 Определяем добавочное сопротивление для второй регулировочной ступени:
,
после приведения к общему знаменателю и некоторых преобразований, получаем
Т. к. скольжение на второй регулировочной ступени равно 0,685 получаем
,
В результате решения квадратного уравнения получаем два корня
,
.
Принимаем
- наибольшее значение из двух корней.
Определяем добавочное сопротивление для второй регулировочной ступени
,
получаем
,
,
где
-
приведенное добавочное сопротивление,
-
добавочное сопротивление на второй
регулировочной ступени.
Механические характеристики имеют вид, изображенный на рисунке 8:
Рисунок 8 Механические характеристики АД в пределах рабочего цикла
3.3.4 Определяем токи ротора на соответствующих ступенях
Ступень 1:
где
Sст1
– скольжение на 1-ой ступени,
Ступень 2:
где
Sст2
– скольжение на 2-ой ступени,
.
3.3.5 Сопротивление Rст1 работает постоянно, а сопротивление Rст2 только на второй ступени. Сопротивления включены последовательно.
3.3.6 Определяем продолжительность включения для ступеней
.
3.3.7 Определяем расчетные токи, средние за время работы
,
,
3.3.8 Определяем каталожный ток для каждой ступени
,
.
3.3.9 Выбираем ящики сопротивлений для каждой ступени по наибольшему току, удовлетворяющему условию Iдоп > Iкат.расч и, зная требуемые значения сопротивлений Rст1, R`ст2, определяем реальные значения требуемых сопротивлений.
Выбираем следующий ящик резисторов 55, у которого продолжительный ток 64А, сопротивление элемента 0,055 Ом и число элементов в ящике 20.
Для первой ступени:
Таким образом получаем, что на 1-ой ступени Rр.доб.1=0,851Ом
Рисунок 9 – Схема соединений резисторов в ящике на первой ступени
,
Для
пуска:
,
Рисунок 10 – Схема соединений резисторов в ящике на пусковой характеристике
Для второй ступени:
Рисунок 11 – Схема соединений резисторов в ящике на второй ступени
