1. Основные характеристики радиосигналов (длительность, полоса частот, мощность, энергия, корреляционная функция, функция неопределённости, диаграмма неопределённости, база).

Длительность сигнала определяется как основание прямоугольника, площадь которого равна площади под кривой квадрата амплитудного закона модуляции:

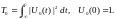
Мощность сигнала определяется как усредненная во времени мгновенная мощность сигнала

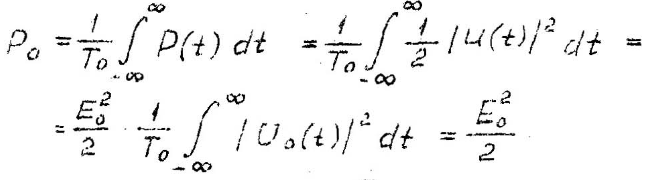
Энергия сигнала определяется как проинтегрированная во времени мгновенная мощность сигнала

Спектр сигнала характеризует распределение комплексных амплитуд (амплитуд и фаз) спектральных составляющих по частоте и определяется как прямое преобразование Фурье от сигнала:

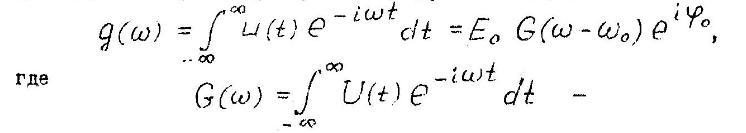
Спектр закона модуляции сигнала.

Таким образом, спектр сигнала есть смещённый по частоте на величину несущей частоты 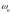спектр закона модуляции сигнала.

Корреляционная функция сигнала есть усредненное во времени произведение двух сигналов, рассовмещённых по времени на величину :

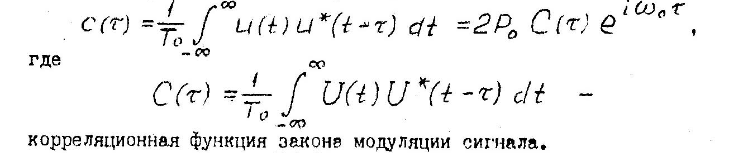
АКФ – произведение сигнала на самого себя, рассовмещённых по времени.

ВКФ – произведение разных сигналов.

Энергетический спектр сигнала характеризует распределение мощности спектральных составляющих по частоте и определяется как прямое преобразование Фурье от корреляционной функции сигнала:

Энергетический спектр пропорционален квадрату амплитудно-частотного спектра сигнала

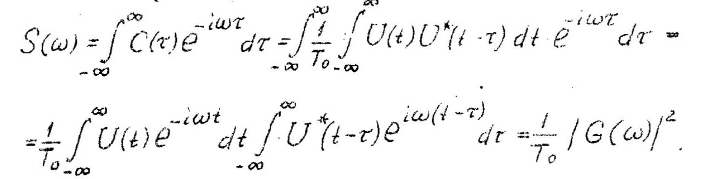
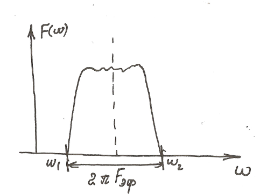
Полоса частот сигнала определяется как основание прямоугольника, площадь которого равна площади под кривой энергетического спектра при одинаковой высоте.

- для видеосигнала.

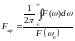- для радиосигнала.

Функция неопределённости сигнала есть квадрат модуля двумерной автокорреляционной функцией сигнала

Функция неопределённости в общем случае представляется поверхностью неопределённостью.

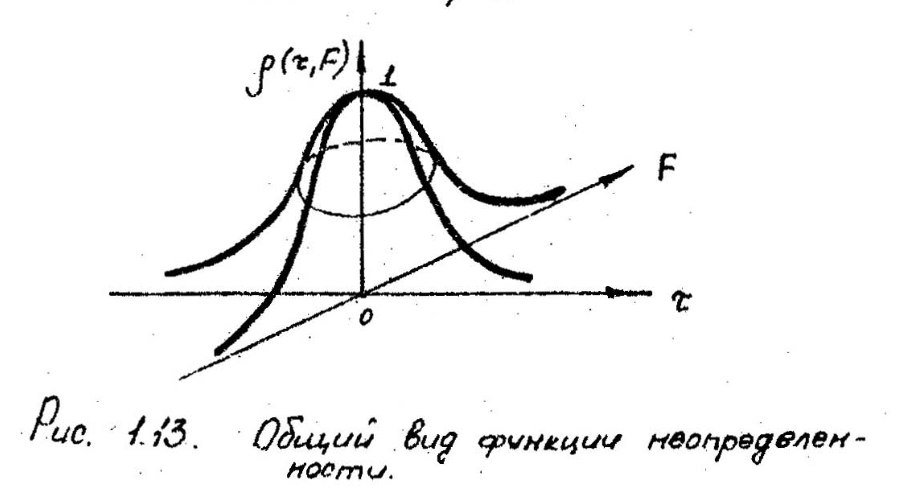
При этом функция неопределённости является нормированной

Свойства функции неопределённости:

1. Сечение функции неопределённости плоскостью F=0 (вдоль оси ) есть квадрат модуля корреляционной функции:

2. Сечение функции неопределённости плоскостью 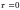есть нормированный энергетический спектр квадрата амплитудного закона модуляции:

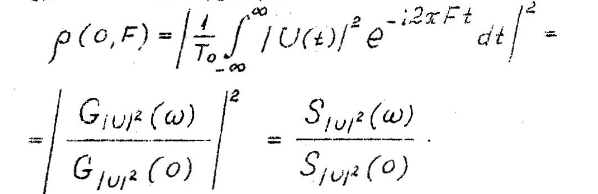
Ширина сечения обратно пропорциональна длительности сигнала?

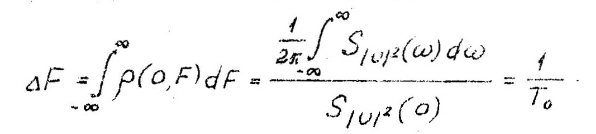
3. Свойство центрально симметрии

.

4. Объём тела неопределённости равен единице:

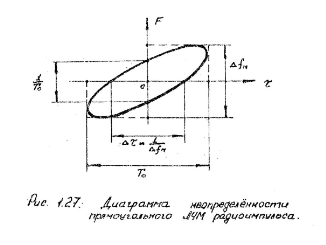
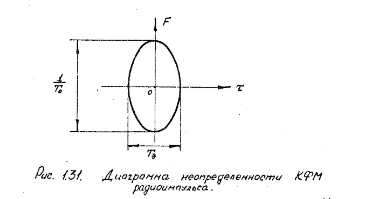
Диаграмма неопределённости – сечение поверзности неопределённости горизонтальной плоскостью, параллельной плоскости 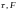. Диаграмма неопределённости имеет вид эллипса.

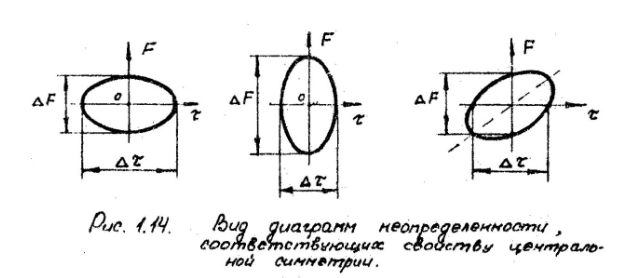
База сигнала

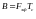, для простых сигналов база равна 1, для сложных В>1.

Сложные сигналы – ЛЧМ, КФМ.

2. Сложные сигналы. Особенности применения сложных сигналов в тсрэзи.

Сложными (широкополосными) сигналами называют сигналы, у которых база В» 1.

Все сложные сигналы с помощью специальных устройств можно сжать по длительности. Коэффициент сжатия определяется базой сигнала. В совре­менных РТС нашли применение детерминированные сложные сигналы, как с непрерывной, так и с дискретной модуляцией.

Среди сигналов с непрерывной модуляцией наибольшее распространение получили сигналы с линейной частотной модуляцией (ЛЧМ-сигналы). Из сложных сигналов с дискретными видами модуляции рассмотрим псевдослу­чайные сигналы с дискретными фазовой и частотной модуляциями.

У ЛЧМ-сигналов расширение спектров осуществляется за счет девиации частоты по линейному закону в пределах длительности сигнала.

Описание ЛЧМ-сигнала можно представить следующим образом:

k=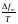

При эффективная полоса частот сигнала .

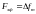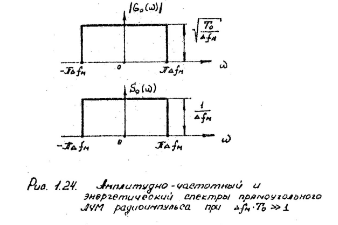
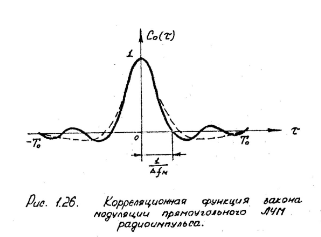
Широкое распространение получили псевдослучайные сигналы с дис­кретной фазовой модуляцией (ПС-сигналы). Аналитическое описание сигнала следующее:

N- количество символов в длительности Т сигнала, 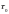- длительность символа, - дискретное значение фазы.

База сигнала в данном случае равна N.

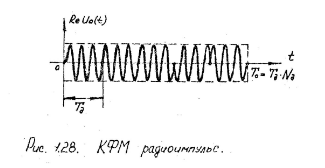
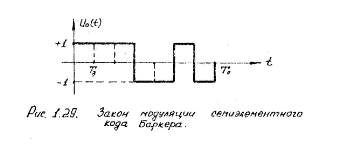
Особенности сложного сигнала:

- способность сжиматься

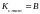
- cпособность расширять полосу частот сигнала (что ведёт к энергетической и структурной скрытности передаваемого сигнала ( в основном для ПС-сигнала))

3. ПС-сигналы с дискретной ФМ. М-последовательности (описание, генерирование , структурно-корреляционные и спектральные свойства).

Бинарные, линейные, рекурентные последовательности максимального периода, которые описываются неприводимым примитивными полиномами вида .

На основе полинома строится рекурентная формула

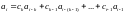
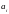{ }, i=1,N.

Суммирование осуществляется по модулю 2.

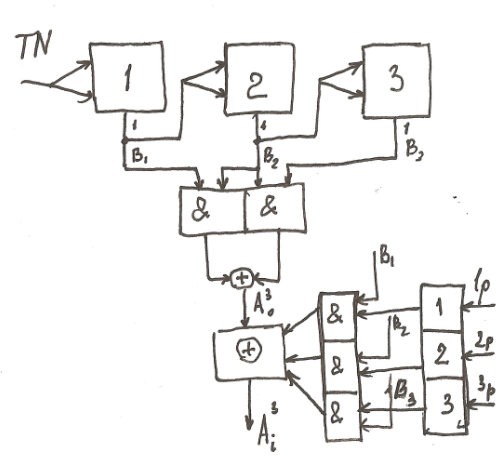
Генерирование М-последовательность на регистрах сдвига для полинома

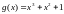
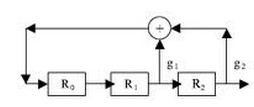(на рисунке сместо g уместнее написать c)

Свойства М-последовательности:

1. N= - значтность, k- порядок.

2. Если М-последовательность в поле (0,1), то кол-во «1» на единицу больше, чем количество «0» (в один период).

3. В М-посл. Писутствуют все двоичные k-разрядные комбинации за исключением «все нули».

4. Количество М-посл. одной значности , где функция Эйлера.

5. Если заданную М-последовательность в поле {0,1}сложить по модулю 2 с её цикл. Сдвигом, то получим ту же М-посл., но с другим цикл. сдвигом.

6. Корреляционная функция

АКФ

7. Спектр.

Энергетический спектр одиночной М-последовательности:

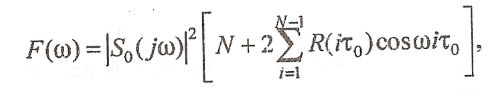
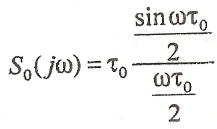
Э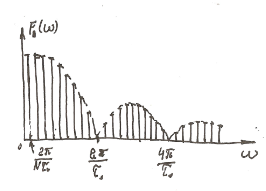 нергетический спектр периодической М-последовательности

4. ПС-сигналы с дискретной ФМ. Четверичнокодированные последовательности (описание, генерирование , классификация, структурно-корреляционные и спектральные свойства).

Бинарная нелинейная полиномиальная последовательность значности .

Свойства ЧКП:

1. Значность .

2. Количество ЧКП одной значности z=N.

3. Формирование ЧКП

а.) аналитически;

б.) алгоритмическим способом

в.) с помощью матрицы Адамара.

а.)

б.) 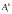, k –порядок, i – номер последовательности.

1.) Номер последовательности представляется в k-разрядной двоичной форме.

2.) Анализируются разряды двоичного номера.

- если первый разряд двоичного номера - «0», то записываются два символа 11;

- если первый разряд двоичного номера – «1», то записываются два символа 10;

- для всех последующих разрядов двоичного номера, начиная со второго, нулю соответствует приписывание к исходной комбинации такой же по размеру комбинации, но отличающейся от исходной инвертированной во второй половине, а единице – инвертирование первой половины приписываемой комбинации.

3. Каждой ЧКП соответствует смежная , причём |i-j|=1. У смежных последовательностей символы, стоящие на нечётных позициях, совпадают, и не совпадают символы, стоящие на чётных позициях.

4. Каждой ЧКП соответствует парная , причём |i-j|=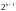 . У парной последовательности первая половина символов совпадает, вторая противоположна.

Пр.

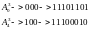
4. Любую ЧКП можно получить путём присоединения парных ЧКП .

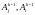5. Любую ЧКП можно получить путём перемеживания смежных ЧКП .

6. Корреляционная функция.

Для одиночной ЧКП

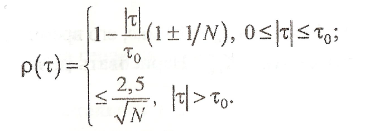
Причем АКФ при чётных сдвигах принимает нулевые значения.

Для периодической ЧКП

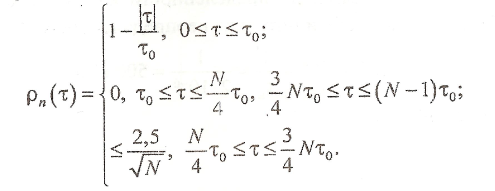
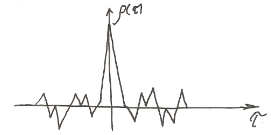
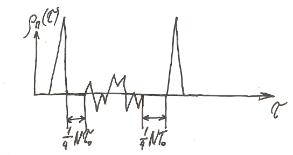
7. Все ЧКП одной значности взаимноортагональны .

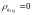8. П арные и смежные ЧКП образуют пару дополнительных последовательностей. Дополнительная серия – две последовательности одной значности, у которой боковые остатки АКФ равны по абсолютной величине и противоположны по знаку.

9. Спектр.

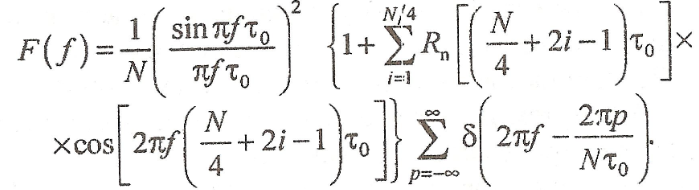
5. ПС-сигналы с дискретной ЧМ (описание, генерирование, классификация, структурно-корреляционные и спектральные свойства).

Аналитически:

,

N- количество дискретных частот,

- длительность дискрет,

- номер i-ой частоты, следующий по псевдослучайному закону.

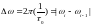
Генерирование:

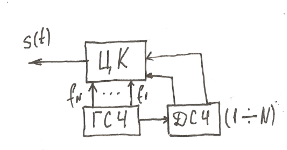
ЦК – цифровой кодер

ДСЧ – датчик случайных чисел

ГСЧ – генератор сетки частот

В зависимости от ГСЧ сигналы ДЧМ делятся на:

- сигналы с когерентной сеткой частот;

- сигналы с некогерентной сеткой частот.

Свойства:

1. База

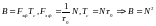
2. Количество ДЧМн сигналов одной значности - все они квазиортоганальны.

3. Корреляционная функция:

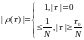
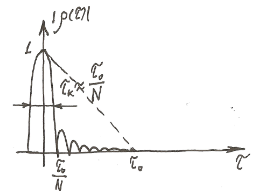
4. Спектр сигнала