Негосударственное образовательное учреждение

пермский гуманитарно-технологический институт

Гуманитарный факультет

Кафедра психологии

МЕТОДИЧЕСКОЕ ПОСОБИЕ

по выполнению контрольных работ по дисциплине «Математика»

для студентов специальности 030301 «Психология»

заочной формы обучения

Пермь, 2006 г.

Математка: Метод. Указ. По выполн. Контр. Раб. По дисц. «Математика» для студ. Спец-ти 030301 «Психология» заочн. Ф. Обучения / Сост. Калашникова л.А. – Пермь: риг ноу пгти, 2006 – … с.

Составитель: Калашникова Л.А.

Методические указания составлены в соответствии с рабочей программой дисциплины «Математика» и учебным планом ПГТИ.

© НОУ «Пермский гуманитарно-технологический институт», 2006

Методические рекомендации по изучению тем курса и выполнению контрольных работ №1, №2, №3.

1. Требования к оформлению контрольных работ.

1. Контрольные работы следует выполнять в ученической тетради. На обложке необходимо указать: номер контрольной работы, специальность, Ф.И.О. и шифр студента.

2. На каждой странице оставить поля для оценки задач и методических указаний проверяющего работу.

3. Условия задач необходимо записать полностью. Решение задач выполнять с необходимыми пояснениями. Если возможно, выполнить проверку результата решения.

4. Прежде чем приступить к решению, необходимо изучить теоретический материал по учебникам и учебным пособиям.

5. Условия задач, входящих в контрольную работу, одинаковы для всех студентов, однако числовые данные задач зависят от личного шифра студента, выполняющего работу. Личный шифр студента устанавливает преподаватель, выдающий задание на контрольную работу.

Тема I. Элементы теории множеств

Выполнение задания по данной теме необходимо начать с изучения основных положений теории множеств. Для изучения вопросов: 1) основные определения, понятия;

2) законы множеств

Можно использовать литературу:

1. Бутузов В.Ф. и др. Математика для гуманитариев, М., 1996.

2. Болтянский В.Г. и др. Математика, Минск, 1996.

1. Множество, элементы множества, пустое множество

В математике множеством называют совокупность, набор каких-либо предметов (объектов).

Предметы, составляющие множество, называются элементами его. То, что элемент «а» входит в множество А, записывается так: (читается: а есть элемент множества А). Запись означает, что элемент «а» не принадлежит множеству А. Термин «множество» означает и употребляется независимо от того, много в этом множестве элементов или мало. Множество, не содержащее ни одного элемента, называется пустым и обозначается символом Æ.

2. Равенство множеств. Подмножество. Универсальное множество. Дополнение множеств.

Если А и В два множества, то запись А=В означает, что они состоят из одних и тех же элементов. Если каждый элемент множества А является в то же время элементов множества В, то говорят, что А - подмножество в В, и пишут . Каждое непустое множество имеет по крайней мере два подмножества: пустое множество Æ и само множество А.

Если одновременно с отношением имеет место отношение , то А=В. То есть, если одновременно А есть подмножество В и В есть подмножество А, то такие два множества равны.

Отношения между множествами наглядно иллюстрируются с помощью так называемых диаграмм Венна.

Диаграмма Венна – это замкнутая линия, внутри которой расположены элементы данного множества, а снаружи - элементы, не принадлежащие этому множеству. Например, диаграмма множества

+

А

В

В

О

А

тношение

Пусть нам дано какое-либо множество Е. Будем рассматривать всевозможные подмножества данного множества Е. Исходное множество Е в таком случае называют универсальным множеством. В качестве примера можно взять множество книг. В это множество входят подмножества научных, художественных книг, книг по искусству и т.д.

Доказано, что универсальное множество Е, состоящее из n элементов, имеет 2ⁿ подмножеств.

Пусть множество А есть некоторое подмножество универсального множества Е. Тогда множество , состоящее из всех элементов множества Е, не принадлежащих множеству А, называется дополнением множества А.

3. Операции над множествами: объединение, пересечение, разность.

1) Объединением С двух множеств А и В называется множество, состоящее из всех элементов, принадлежащих множеству А или множеству В. Обозначают это так: .

На диаграммах Венна это имеет вид:

2) Пересечением С двух множеств А и В называется множество, состоящее из элементов, принадлежащих множеству А и множеству В одновременно. Обозначают это так: . Иными словами, пересечение образовано всеми общими элементами данных множеств. Аналогично определяется пересечение трех и более множеств. На диаграммах заштрихованные множества – это пересечение двух и трех множеств.

Примеры: 1. Множество успевающих учеников в классе – А, В – множество девочек в этом классе, С – множество неуспевающих учеников в классе. Тогда - множество учеников этого класса.

Пример 2: А – множество мальчиков, обучающихся в данной школе, а В – множество всех учеников из 10-го класса. Тогда пересечение - множество мальчиков, которые учатся в этом классе.

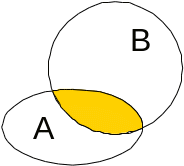
3) Разностью С двух множеств А и В называется множество, состоящее из всех элементов А, не входящих в В. Обозначают это так: Таким образом, из множества А достаточно удалить общие элементы множества А и В, то есть все элементы , чтобы получить разность На диаграмма – заштрихованные части есть

Примеры: Если А – множество всех учащихся 8-го класса данной школы, а В – множество всех девочек, которые учатся в школе, то - множество всех мальчиков, которые обучаются в этом 8-ом классе.

4. Основные законы операций над множествами

1) и - переместительные законы объединения и пересечения множеств.

2) и - сочетательные законы объединения и пересечения множеств.

3) Æ = А, Æ = Æ, А \ Æ = А, А \ А = Æ.

4) Æ, Е \ А , А \ Е = Æ, , , .

5) - распределительный закон пересечения относительно объединения; - распределительный закон объединения относительно пересечения.

На диаграммах:

Пример. 20 учеников – двое изучают только английский язык, 3 – только немецкий, 6 – французский. Никто (0) не изучает 3-х языков; 1 изучает немецкий и английский языки; 3 – французский и английский. Сколько учеников изучают французский и немецкий.

Решение. Обозначим через А – множество всех учеников, изучающих английский язык, В – немецкий, С – французский. По условию - пересечение А и В содержит 1 элемент,

- пересечение А с С – 3 элемента, - пересечение А с В и с С - Æ - пустое множеств (пусто). Требуется определить количество элементов в пересечении - изучают французский и немецкий.

Покажем на диаграмме Венна:

- содержит 20 элементов. Множество должно содержать: 20-1-2-3-6-3= 5 учеников (смотри диаграмму).