2. Средняя простая

(4)

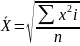(5)

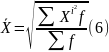
Применяется когда производство либо =1 либо одинаково

Кроме производственного среднего применяется среднее геометрическое , будет далее ряды динамики для определения средних размеров – используют средне кубическое.

2.3Средняя квадратичная

Средне геометрические будут далее в теме «геометрические динамики»

Применятся для определенных средних размеров,

Свойства средней арифметической:

Вычисление среднеарифметического частного сопряженного с большими затратами времени. Процедуру расчета можно упростить , если выскользнув след свойствами:

1)Ср. арифметические из пост чисел= этому постоянному.

2)Если все пропорционально изменить, то средне арифметическое не изменится.

3)Если все варианты уменьшить или увеличить на одно и тоже число, то все уменьшится или увеличится на одинаковое кол-во раз.

4)Если все варианты увеличится или уменьшить в один число раз, то среднее тоже увеличится или уменьшится в тоже число раз.

Таблица 1

№	Районы Брянска	Число школ	Ср. число уч в шк	Средне чисто уч приходит.
1	Бежецкий	18	1200	32
2	Советский	20	800	40
3	Володарка	14	1050	38
4	Фокинский	12	980	45
		Х1?	Х2?	Х3?

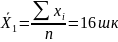
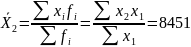в школе

Среднее число учащихся на 1 учителя = среднее число учащихся в школах/ среднее число учащихся приход на 1 учит

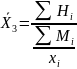
Лекция №6 Дата: 8.10.12

Тема 6: Структурные средние

Помимо средних существует система структурных показателей: мода и

Медианна

М (мода) наиболее часто встречающийся вариант ряда

В дискретном ряду мода определяется , как значение признака с наиболее частной без вычисления определения моды не представляет трудностей.

Таблица 1

Размер обуви	33	34	35	36	37	38	39	итого
Число пар	10	48	187	54	82	79	43	500

1.1 Модой является 35 размер обуви .так как этого размера больше всего

1.2 Мода для инертно ряда определяется по приблизительной формуле

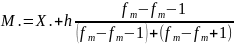(1)

Х.-нижняя граница предельного интегрирования

h- величина

Fm – частного модельного интегрирования

Fm-₁ –предмет модельного

Fm+₁ – предмет следующий за модельным

Распространение студентов по возрасту Таблица 1

Возрастные группы	До 20	20-25	25-30	30-35	35-40	40-45	>45
Число студентов	346	872	1054	787	212	121	76
Сумма неконечных подсчетов	346	1218	2272	3053	3265	3386	4362

Для начисления модуля в интервальном ряду в начале определяют модульный интервал, в пределах которого находится мода

Затем находят приближенное значение модальной величины признака по формуле (1)

Т.к на интервале 25-30 существует наиболее частного (1054) модельный интервал будет находится в этих пределах.

M.=1054-872/25+5(1054-872)+(1054+781)= 27 (лет)

Это означает , что модульный возраст составляет 27 лет.

Это означает ,т.о мода наиболее привычная величина распределения.

Мода- средняя величина по-разному характеризуют совокупности в целом и мода по обобщающему значению уступает ей.

Мода-это описательная характеристика, она описывает количество, структуру , строение

Ме(медиана) – это вариант который приходит на середину ряда, расположенного в порядке возрастания или убывания чисел значений признаков.

Медиана делит ряд на 2 равные части.

Для интервального вариационного ряда алгоритм определения методологии в следующем.

1. Определить модельный интервал на которою приходится медиана.

2. По приближенной формуле определим медиану.

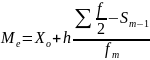(2)

Х₀- нижняя граница интервала который содержит медиану.

H - величина интервала.

Сумма∑ F - сумма частот или число членов ряда

Sm-₁ – сумма накопленных частот для предшествующая медианному.

Fm – частота медианного интервала.

Сумма∑ F = 3 462

Сумма ∑F/2 = 1731

Это означает , что медиальный интервал находится в переделах 35-30 лет

Ме= 25+5=1731-1216/154=27,4(лет)

Это означат что одна половина имеет возраст до 27,4 лети , а вторая больше.

Медиана , так же ка и мода является ,описательной характеристикой.

Пример 1

Таблица: распределение игр чемпионата России по футбола по числу забитых мячей.

Число забитых мячей	Число игр
0 1 2 3 4 5 6 7 8	21 41 41 37 19 10 6 3 2
Сумма = 130 Определить моду и медиану. M0=0.5 Me=2

Лекция № 7 Дата:15.10.12

Тема.7 Выборочное наблюдение.

1. Понятие выборочного наблюдения, цель и принципы его применения.

2. Основные характеристики выборочной и генеральной совокупности.

3. Ошибки выборочного наблюдения.

4. Виды и схемы отбора.

5. Определение необходимой численности выборки.

Вопрос №1

Понятие выборочного наблюдения, цель и принципы его применения.

Так как статистика имеет долю с массовыми совокупностями, стат. Исследования очень трудоемкие. Поэтому целесообразно и возможно заменять сплошное наблюдение выборочным.

ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ – несплошное наблюдение единиц изучаемой совокупности, отобранная случайным способом по определенным правилам выборки.

ЦЕЛЬ ВЫБОРКИ – на основе выборочных характеристик (средних и относительных) Получить обобщающие показатели генеральной совокупности.

Причины применения связаны с трудоемкостью стат. Исследования и целесообразностью.

Вся совокупность единиц, из которых, производится отбор, называется ГЕНЕРАЛЬНОЙ и обозначается N.

Часть совокупности, попавшая в выборку, называется ВЫБОРОЧНОЙ и обозначается n.

Вопрос №2.

Символы основных характеристик генеральной и выборочной совокупности.

№	Характеристики	Генеральная совокупность	Выборочная совокупность
1.	Объем совокупности (числ. ед.)	N	n
2.	Численность единиц, обладающая обследуемым признаком	М	m
3.	Доля единиц, обладающая признаком	P= M/N	W=m/n
4.	Средний размер признака	ẋ=∑xi/N	ẋ=∑xi/n
5.	Дисперсия количественного признака	Gẋ2=∑(xi-ẋ)2/N	Gẋ2=∑(xi-ẋ)2/n
6.	Дисперсия доля	Gp2=pq, где q=p=1	Gẋ2=W(1-N)
7.	Доля отбора	Д= n/N	Д=N/n

Вопрос №3.

Ошибка выборочного наблюдения.

Т. к обследованиям подвергается часть совокупности, неизбежна ошибка, погрешность.

Существует 2 основных вида ошибок:

1. Ошибка регистрации (случайная, систематическая, (можно избавиться))

2. Ошибка репрезентативности (присущи выб. наблюдению (нельзя избавиться))

Используют определенные методики, ошибки репрезентативности можно свести к минимуму.

В теории уменьшения данных ошибок, различают СРЕДНЮЮ и ПРЕДЕЛЬНУЮ ошибки.

По теории Чебышева доказано, что величина ошибки не должна превышать (формула1)- −∆пр = Tm(1)

Предельная ошибка выборки, а (формула2)- средняя ошибка M=√G²/n(2)

t- коэффициент доверия (множитель или показатель кратности средней ошибки, связанных с вероятностью)

В спец. математических таблицах приводятся зависимости коэф. Доверия и вероятности, связанных с этим значением.

t=1 Ф(t)=0,683

t=1.5 Ф(t)=0,866

t=2 Ф(t)=0,954

t=2.5 Ф(t)=0,988

t=3 Ф(t)=0,997

t=3.5 Ф(t)=0,999

Величина средней ошибки в выборке рассчитывается дифференцированно в зависимости от способа и процедуры выборки (ф.1) применяется при случайном повторном отборе.

При бесповторном отборе используют:

M=G/n(3)

Расчет средней и предельной ошибки выборки позволяет определить возможные пределы в которых будут находиться характеристики генеральной совокупности.

M=√G²/n(1-n/N)(4)

Вопрос №4.

Виды и схемы отбора.

Формирование выборочной совокупности может осуществляться по-разному: в зависимости от вида схемы отбора, изменения единицы отбора и т. д.

Существует 4 вида отбора:

1. Собственно-случайный - из общего количества данных наугад

2. Механический– вся совокупность разбивается на равные объема и из каждой группы берется одна единица. Предварительно все единицы в каждой группе выстраиваются в определенном порядке.

3. Типический– совокупность расчленяется по сущ. типическому признака качественно однородные группы, затем из каждой группы собственно-случайным или механическим способом, отбирается количество единиц пропорциональное удельному весу группы во всей совокупности.

Типический отбор дает наиболее точный результат, выборка более репрезентативна и представительна.

4. Серийный- отбирается не единица, а серия. В каждой группе серий проводится сплошное наблюдение. Результат переносится на совокупность. Серийный отбор организовывать легче, но ошибка в выборке больше.

СХЕМЫ ОТБОРА:

1. Повторный отбор – каждая отобранная единица возвращается назад.

2. Бесповторный отбор – каждая отобранная единица не возвращается назад.