№25 Диметрия

Диметрия — вид аксонометрической проекции. Аксонометрия позволяет с помощью одного объемного изображения видеть предмет сразу в трех измерениях. Получение объемного представления сопровождается определенным искажением размеров объекта вдоль осей. В диметрии коэффициенты искажения размеров по двум осям одинаковы, отсюда и название — диметрия.

Существует два вида диметрии: прямоугольная и косоугольная фронтальная. При выполнении любой диметрической проекции все размеры вдоль оси X делятся пополам, а размеры по осям Y и Z остаются кратными единице. Т.е коэффициент искажения по оси Х принимается равным 0.5, а по оси Z и Y искажения размеров нет

Начертите оси для построения изображения детали в диметрии. В прямоугольной диметрии углы между осями Z и X составляют 97о10'. Углы между осями Y и Z — 131о25'; углы между осями Y и X — 127о50'. Во фронтальной диметрии углы между осями Z и X составляют девяностоградусов. А между осями Z и Y; X и Y — сто тридцать пять градусов.

№24 АКСОНОМЕТРИЯ

(от греч. axon - ось и …метрия), способ изображения предметов на чертеже при помощи параллельных проекций, состоящий в том, что предмет изображается на плоскости вместе с пространственной системой координат, к которой он отнесен, и его проекцией на одну из координатных плоскостей.

Виды аксонометрических проекций. 

1) изометрические, т.е. одинакового измерения (оси z', х' и у' наклонены одинаково; следовательно, уменьшение размеров по направлению всех трех осей одинаковое); 2) диметрические, т. е. двойного измерения (две оси координат имеют один и тот же наклон, а третья - другой; следовательно, уменьшение размеров по этим двум осям будет одно и то же, а по третьей оси - другое); 3) триметрические, т.е. тройного измерения (все оси имеют разный наклон; следовательно, уменьшение размеров по направлению всех трех осей разное). В машиностроительном черчении из прямоугольных аксонометрических проекций чаще всего применяют изометрическую и диметриче-скую, а из косоугольных - диметрическую, которую иначе называют фронтальной диметрической проекцией.

Аксонометрия делится на три вида:   1. Изометрия (измерение по всем трем координатным осям одинаковое).   2. Диметрия (измерение по двум координатным осям одинаковое, а по третьей — другое).   3. Триметрия (измерение по всем трем осям различное). В каждом из этих видов проецирование может быть прямоугольным и косоугольным. аксонометрия широко применяется в изданиях технической литературы и в научно-популярных книгах благодаря своей наглядности

Изображение аксонометрических осей и показатели искажения. В изометрической проекции углы между аксонометрическими осями х' , у' и z'одинаковы (по 120°); ось z' расположена вертикально; следовательно, оси х'и у' наклонены к горизонтальной линии на угол 30° (фиг.271,а).

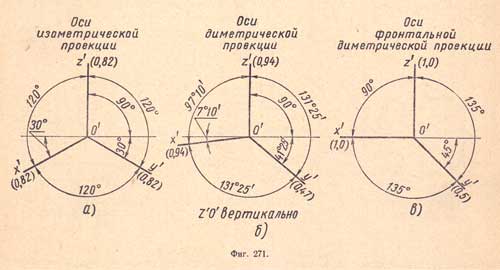
При таком положении осей показатели искажения для всех осей одинаковы и равны 0,82. Показателем искажения называют отношение размера аксонометрической проекции отрезка, имеющего направление какой-либо оси координат, к его действительному размеру. Например, при действительном размере 100 мм и показателе искажения 0,82 размер аксонометрической проекции равен 100 × 0,82 = 82 мм. В диметрической проекции угол между аксонометрическими осями z' и х'равен 97°10', а углы между аксонометрическими осями х' и у', а также z' и у'одинаковы, т.е. по 131°25'. Аксонометрическая ось z' имеет вертикальное положение, следовательно, ось х' наклонена к горизонтальной линии на угол7°10' а ось у' на угол 41° 25' (фиг.271,б). При таком наклоне аксонометрических осей показатель искажения для осей z'и х' равен 0,94, а для оси у' - 0,47. Во фронтальной диметрической проекции угол между аксонометрическими осями z' и х' равен 90°, а углы между аксонометрическими осями х' и у', а также между аксонометрическими осями z' и y' одинаковы, т. е. по 135°. Осьz' имеет вертикальное положение, следовательно, ось х' будет иметь горизонтальное положение, а ось у' наклонена к горизонтальной линии на угол 45° (фиг.271,в). Показатели искажения по аксонометрическим осям х' и z' равны 1,0 а по осиу' - 0,5. Такую фронтальную диметрическую проекцию называют кабинетной; ее рекомендуется применять тогда, когда хотят показать без изменения очертания фигур, расположенных в плоскостях, параллельных фронтальной плоскости проекций. Для сравнения изображений, выполненных в аксонометрических проекциях, на (фиг.272) показаны различные аксонометрические проекции одного и того же куба.

№26 Триметрия

Триметрия, диметрия и изометрия могут быть как прямоугольными, так и косоугольными. [1]

Косоугольная триметрия на практике не используется. [2]

При триметрии длины проекций попарно различны. [3]

Изометрия, диметрия и триметрия могут быть прямоугольными или косоугольными. [4]

Аксонометрия называется тримет-рической, или триметрией, если все показатели искажения различны. [5]

Если все коэффициенты искажения различны ( при трех разных наклонах осей), получается малоприменяемая триметрия. [6]

Так как единицы аксонометрических масштабов по всем осям различны, то аксонометрия представляет собойтриметрию. [7]

При построении изображений предметов в косоугольной аксонометрии используют, как; правило, изометрию и димет-рию; косоугольная триметрия встречается редко, поэтому мы не будем ее описывать. Плоскость аксонометрических проекций в косоугольной аксонометрии занимает обычно частное расположение относительно координатных плоскостей. [8]

Нетрудно видеть, что если треугольник следов равносторонний, то аксонометрия является изометрией, если он равнобедренный - диметрией; в случае разностороннего треугольника, аксонометрия представляет собойтриметрию. Обратите внимание на то, что приведенные утверждения относятся только к прямоугольной аксонометрии. [9]

Если аксонометрия является изометрией, то аксонометрические масштабы по всем осям равны между собой, в случае диметрии - два масштаба равны, но ОТЛИЧНЬЙУГ третьего, и при триметрии ни один масштаб не равен другому. [10]

Если треугольник следов разносторонний, то отрезки О Х, О У и O Z не равны между собой, следовательно, коэффициенты искажения по аксонометрическим осям различны, и аксонометрия является триметрией. При равнобедренном треугольнике следов аксонометрия становится диметрией, при равностороннем - изометрией. [11]

Книга содержит большое количество чертежей. Значительная часть стереометрических чертежей выполнена в ди-метрии, там, где это необходимо, применялась триметрия. Авторы стремились давать наглядные чертежи-рисунки, поэтому на чертежах многогранники часто изображаются не как твердые тела, а как пустотелые многогранные поверхности. При этом обычно одна из граней делается прозрачной - через нее видны линии и плоскости, проходящие внутри многогранника. На некоторых чертежах многогранники изображены проволочными - на этих чертежах дается только скелет из ребер. В книге приведены также шесть фотографий моделей правильных и почти правильных звездчатых многогранников. [12]

В зависимости от направления проецирования аксонометрические проекции делятся на прямоугольные и косоугольные. Показатели искажения в общем случае отличаются друг от друга; тогда аксонометрия называется триметрией. Если два показателя искажения равны друг другу, то аксонометрия носит название диметрия. [13]

Через вершины треугольника проводим высоты. Далее необходимо определить показатели искажения по ним. Треугольник следов можно рассматривать как основание пирамиды, грани которой при вершине имеют прямые углы, а точку 0 0-как ортогональную проекцию вершины этой пирамиды. Тогда высоты треугольника следов О Кх, О Ку и O K z будут ортогональными проекциями ребер пирамиды, которые и определяют аксонометрические оси х, у и г прямоугольной триметрии. [14]

Построение плоскости аксонометрических проекций и треугольника следов выполнено на том же чертеже. Совместив треугольник следов с горизонтальной плоскостью, вращая его вокруг следа XY, найдем натуральную величину этого треугольника, а затем и аксонометрические оси. Для построения аксонометрии предмета ( на чертеже построены также аксонометрические масштабы) воспользуемся показателями искажения. Показатели искажения различны, следовательно, аксонометрией является прямоугольная триметрия. Проверим правильность выполненных подсчетов по формуле, приведенной на стр. [15]

№23 Классификация проекций

 

В общем случае проекции преобразуют точки, заданные в системе координат размерностью  n, в системы координат размерностью меньше чем  n.

Будем  рассматривать случай проецирования трех измерений в два. Проекция трехмерного объекта (представленного в виде совокупности точек) строится при помощи прямых проекционных лучей, которые называются проекторами и которые проходят через каждую точку объекта и, пересекая картинную плоскость, образуют проекцию.

 

 

Рис.  3.7. Центральная и параллельная проекции

Определенный таким образом класс проекций существует под названием плоских геометрических проекций, так как проецирование производится на плоскость, а не на искривленную поверхность и в качестве проекторов используются прямые, а не кривые линии.

Многие картографические проекции являются либо не плоскими, либо не геометрическими.

Плоские геометрические проекции в дальнейшем будем называть просто проекциями.

Проекции делятся на два основных класса (рис. 3.7):

        параллельные (аксонометрические);

        центральные (перспективные).

 Полная классификация проекций приведена на рис. 3.8.

Рис. 3.8. Классификация проекций

Параллельные проекции делятся на два типа в зависимости от соотношения между направлением проецирования и нормалью к проекционной плоскости (рис. 3.9.):

1)       ортографические – направления совпадают, т. е. направление проецирования является нормалью к проекционной плоскости;  

2)       косоугольные – направление проецирования и нормаль к проекционной плоскости не совпадают.

 

Рис.  3.9. Ортографические и косоугольные проекции

 Наиболее широко используемыми видами ортографических проекций является вид спереди, вид сверху(план) и вид сбоку, в которых картинная плоскость перпендикулярна главным координатным осям. Если проекционные плоскости не перпендикулярны главным координатным осям, то такие проекции называютсяаксонометрическими.

При аксонометрическом проецировании сохраняется параллельность прямых, а углы изменяются; расстояние можно измерить вдоль каждой из главных координатных осей (в общем случае с различными масштабными коэффициентами).

Изометрическая проекция – нормаль к проекционной плоскости, (а следовательно и направление проецирования) составляет равные углы с каждой из главных координатных  осей. Если нормаль к проекционной плоскости имеет координаты (a,b,c), то потребуем, чтобы |a| = |b| = |c|, или a=b=c, т. е. имеется 8 направлений (по одному в каждом из октантов), которые удовлетворяют этому условию. Однако существует лишь 4 различных изометрических проекции (если не рассматривать удаление скрытых линий), так как векторы (a, a, a) и (-a,-a,-a) определяют нормали к одной и той же проекционной плоскости.

Изометрическая проекция (рис. 3.10.) обладает следующим свойством: все 3 главные координатные оси одинаково укорачиваются. Поэтому можно проводить измерения вдоль направления осей с одним и тем же масштабом. Кроме того, главные координатные оси проецируются так, что их проекции составляют равные углы друг с другом (120°).

 

 

Рис. 3.10. Изометрическая проекция единичного куба

Косоугольные (наклонные) проекции сочетают в себе свойства ортографических проекций (видов спереди, сверху и сбоку) со свойствами аксонометрии. В этом случае проекционная плоскость перпендикулярна главной координатной оси, поэтому сторона объекта, параллельная этой плоскости, проецируется так, что можно измерить углы и расстояния. Проецирование других сторон объекта также допускает проведение линейных измерений (но не угловых) вдоль главных осей. Отметим, что нормаль к проекционной плоскости и направление проецирования не совпадают.

Двумя важными видами косоугольных проекций являются проекции:

     Кавалье (cavalier) – горизонтальная косоугольная изометрия (военная перспектива);

     Кабине (cabinet) – фронтальная косоугольная диметрия.

 

Рис. 3.11. Проекция Кавалье

В проекции Кавалье (рис. 3.11.) направление проецирования составляет с плоскостью угол 45. В результате проекция отрезка, перпендикулярного проекционной плоскости, имеет ту же длину, что и сам отрезок, т. е. укорачивание отсутствует.

 

Рис. 3.12. Проекция Кабине

Проекция Кабине (рис. 3.12.) имеет направление проецирования, которое составляет с проекционной плоскостью угол   = arctg(½) (≈26,5°). При этом отрезки, перпендикулярные проекционной плоскости, после проецирования составляют ½ их действительной длины. Проекции Кабине являются более реалистическими, чем проекции Кавалье, так как укорачивание с коэффициентом ½ больше согласуется с нашим визуальным опытом.

Центральная проекция любой совокупности параллельных прямых, которые не параллельны проекционной плоскости, будет сходиться в точке схода. Точек схода бесконечно много. Если совокупность прямых параллельна одной из главных координатных осей, то их точка схода называется главной точкой схода. Имеются только три такие точки, соответствующие пересечениям главных координатных осей с проекционной плоскостью. Центральные проекции классифицируются в зависимости от числа главных точек схода, которыми они обладают, а следовательно и от числа координатных осей, которые пересекают проекционную плоскость.

1. Одноточечная проекция (рис. 3.13).

 

Рис. 3.13. Одноточечная перспектива

2. Двухточечная проекция широко применяется в архитектурном, инженерном и промышленном проектировании.

3. Трехточечные центральные проекции почти совсем не используются, во-первых, потому, что их трудно конструировать, а во-вторых, из-за того, что они добавляют мало нового с точки зрения реалистичности по сравнению с двухточечной проекцией.

№22 Проекции.Мировые и экранные координаты.

Проекции

В настоящее время наиболее распространены устройства отображения, кото­рые синтезируют изображения на плоскости — экране дисплея или бумаге. Устройства, которые создают истинно объемные изображения, пока доста­точно редки. Но все чаще появляются сведения о таких разработках, напри­мер, об объемных дисплеях [37] или даже о трехмерных принтерах [45].

При использовании любых графических устройств обычно используют про­екции. Проекция задает способ отображения объектов на графическом уст­ройстве. Мы будем рассматривать только проекции на плоскость.

Мировые и экранные координаты

При отображении пространственных объектов на экране или на листе бумаги с помощью принтера необходимо знать координаты объектов. Мы рассмот­рим две системы координат. Первая — мировые координаты, которые опи­сывают истинное положение объектов в пространстве с заданной точностью. Другая — система координат устройства изображения, в котором осуществ­ляется вывод изображения объектов в заданной проекции.

Пусть мировые координаты будут трехмерными декартовыми координатами. Где должен размещаться центр координат и какими будут единицы измере- ния вдоль каждой оси, пока для нас не очень важно. Важно то, что для ото­бражения мы будем знать какие-то числовые значения координат отображае­мых объектов.

Для получения изображения в определенной проекции необходимо рассчи­тать координаты проекции. Из них можно получить координаты для графи­ческого устройства — назовем их экранными координатами. Для синтеза изображения на плоскости достаточно двумерной системы координат. Одна­ко в некоторых алгоритмах визуализации используются трехмерные экран­ные координаты, например, в алгоритме Z-буфера.

№5 Растровая графика

Компьютерное растровое изображение представляется в виде прямоугольной матрицы, каждая ячейка которой - цветная точка. Т.е. основным элементом растрового изображения является точка. Если изображение экранное, то эта точка называется пикселем.

При создании растровых изображений необходимо задавать разрешение и размеры изображения.

В зависимости от того, какое графическое разрешение экрана используется операционной системой, на экране могут размещаться изображения, имеющие 640х480, 800х600, 1024х768 и более пикселей.

Разрешение изображения измеряется в точках на дюйм (dots per inch - dpi) (1 дюйм = 25,4 мм). Полиграфическая печать полноцветного изображения требует разрешения не менее 200-300 dpi.

С помощью растровой графики можно отразить и передать всю гамму оттенков и тонких эффектов, присущих реальному изображению. Растровое изображение ближе к фотографии, оно позволяет более точно воспроизводить основные характеристики фотографии: освещенность, прозрачность и глубину резкости.

Чаще всего растровые изображения получают с помощью сканирования фотографий и других изображений, с помощью цифровой фотокамеры или путем "захвата" кадра видеосъемки.

Основным недостатком растровых изображений является невозможность их увеличения для рассмотрения деталей. При увеличении изображения точки становятся крупнее, но дополнительная информация не появляется. Этот эффект называется пикселизацией (см. рисунок 19).

Средства работы с растровой графикой

К числу простейших растровых редакторов относятся PaintBrush, Paint, Painter, которые позволяют непосредственно рисовать простейшие растровые изображения.

Основной класс растровых графических редакторов предназначен для обработки готовых растровых изображений с целью улучшения их качества и создания собственных изображений из уже имеющихся. К таким редакторам относятся такие мощные программы, как Adobe Photoshop, Corel PhotoPaint,Gimp и другие.

Основные растровые форматы

BMP (Windows Device Independent Bitmap) - самый простой растровый формат является форматом Windows, он поддерживается всеми графическими редакторами, работающими под ее управлением. В BMP данные о цвете хранятся только в модели RGB, поддерживаются как индексированные цвета (до 256 цветов), так и полноцветные изображения. Благодаря примитивнейшему алгоритму записи изображения, при обработке файлов формата BMP очень мало расходуется системных ресурсов, поэтому этот формат часто используется для хранения логотипов, экранных заставок, иконок и прочих элементов графического оформления программ.

GIF (Graphics Interchange Format) - является одним из самых популярных форматов изображений, размещаемых на веб-страницах. Отличительной его особенностью является использование режима индексированных цветов (не более 256), что ограничивает область применения формата изображениями, имеющими резкие цветовые переходы. Небольшие размеры файлов изображений обусловлены применением алгоритма сжатия без потерь качества, благодаря чему изображения в этом формате наиболее удобны для пересылки по каналам связи глобальной сети. В GIF реализован эффект прозрачности и возможности хранить в одном файле несколько картинок с указанием времени показа каждой, что используется для создания анимированных изображений.

PNG (Portable Network Graphics) - формат PNG, являющийся плодом трудов сообщества независимых программистов, появился на свет как ответная реакция на переход популярнейшего формата GIF в разряд коммерческих продуктов. Этот формат,  в отличие от GIF сжимает растровые изображения не только по горизонтали, но и по вертикали, что обеспечивает более высокую степень сжатия. Как недостаток формата часто упоминается то, что он не дает возможности создавать анимационные ролики. Зато формат PNG позволяет создавать изображения с 256 уровнями прозрачности что, безусловно, выделяет его на фоне всех существующих в данный момент форматов. Так как формат создавался для Интернета, в его заголовке не предназначено место для дополнительных параметров типа разрешения, поэтому для хранения изображений, подлежащих печати, PNG плохо подходит, для этих целей лучше подойдет PSD или TIFF.

JPEG (Joint Photographic Experts Group) - самый популярный формат для хранения фотографических изображений, является общепризнанным стандартом. JPEG может хранить только 24-битовые полноцветные изображения. Хотя JPEG отлично сжимает фотографии, но это сжатие происходит с потерями и портит качество, тем не менее, он может быть легко настроен на минимальные, практически незаметные для человеческого глаза, потери. Однако не стоит использовать формат JPEG для хранения изображений, подлежащих последующей обработке, так как при каждом сохранении документа в этом формате процесс ухудшения качества изображения носит лавинообразный характер. Наиболее целесообразно будет корректировать изображение в каком-нибудь другом подходящем формате, например TIFF, и лишь по завершению всех работ окончательная версия может быть сохранена в JPEG. Формат JPEG не поддерживает анимацию или прозрачный цвет, и пригоден в подавляющем большинстве случаев только для публикации полноцветных изображений, типа фотографических, в Интернете.

TIFF (Tag Image File Format). Как универсальный формат для хранения растровых изображений, TIFF достаточно широко используется, в первую очередь, в издательских системах, требующих изображения наилучшего качества. Кстати, возможность записи изображений в формате TIFF является одним из признаков высокого класса современных цифровых фотокамер. В этом формате поддерживаются такие чисто профессиональные возможности, как обтравочные контуры, альфа-каналы, возможность сохранять несколько копий изображения с разным разрешением и даже включать в файл слои. Благодаря своей совместимости с большинством профессионального ПО для обработки изображений, формат TIFF очень удобен при переносе изображений между компьютерами различных типов.

PSD (Adobe Photoshop) - является стандартным форматом пакета Adobe Photoshop и отличается от большинства обычных растровых форматов возможностью хранения слоев (layers). Он содержит много дополнительных переменных (не уступает TIFF по их количеству) и сжимает изображения иногда даже сильнее, чем PNG (в тех случаях, когда размеры файла измеряются не в килобайтах, а в десятках или даже сотнях мегабайт). Файлы PSD свободно читаются большинством популярных просмотрщиков.

№6 Векторная графика.

Основным логическим элементом векторной графики является геометрический объект. В качестве объекта принимаются простые геометрические фигуры (так называемые примитивы - прямоугольник, окружность, эллипс, линия). Благодаря этому форму, цвет и пространственное положение составляющих изображение объектов можно описывать с помощью математических формул.

 

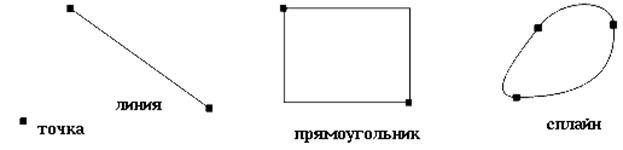
Рис. 44. Геометрические примитивы.

Преимущества векторной графики:

       Она экономна в плане дискового пространства, необходимого для хранения изображений: это связано с тем, что сохраняется не само изображение, а только некоторые основные данные, используя которые, программа всякий раз воссоздает изображение заново.

       Объекты векторной графики легко трансформируются и масштабируются, что не оказывает практически никакого влияния на качество изображения. Масштабирование, поворот, искривление сводятся к элементарным преобразованиям над векторами.

       Программы векторной графики имеют развитые средства интеграции изображений и текста, единый подход к ним. Поэтому программы векторной графики незаменимы в области дизайна, технического рисования, для чертежно-графических и оформительских работ.

Недостатки векторной графики:

       Векторная графика ограничена в живописных средствах: в программах векторной графики практически невозможно создавать фотореалистичные изображения.

       Векторный принцип описания изображения не позволяет автоматизировать ввод графической информации, как это делает сканер для растровой графики.

Средства работы с векторной графикой

Как и в случае с растровой графикой, для работы с векторной имеется огромное количество программных средств, освоение которых сложнее по сравнению с растровыми. К основным относятся программы:

       CorelDraw - это профессиональный графический редактор с богатыми настройками и развитой системой управления.

       Adobe Illustrator - основное достоинство программы в том, что она вместе с Adobe Photoshop и Adobe PageMaker образует достаточно мощный пакет для выполнения компьютерной верстки полиграфических изданий и разработки сложных документов.

       Macromedia Freehand - один из самых дружественных и интуитивно понятных векторных редакторов. Программа отличается простотой системы управления и высоким быстродействием, но ее возможности несколько скромнее, чем у предыдущих редакторов.

Основные векторные графические форматы

Своего рода стандартом стали форматы двух наиболее популярных профессиональных графических пакетов - Adobe Illustrator и CorelDRAW:

AI (Adobe Illustrator Document) - поддерживают практически все программы, так или иначе связанные с векторной графикой. Этот формат является наилучшим посредником при передаче изображений из одной программы в другую, с РС на Macintosh и наоборот. В целом, несколько уступая CorelDRAW по иллюстративным возможностям, (может содержать в одном файле только одну страницу, имеет маленькое рабочее поле - этот параметр очень важен для наружной рекламы - всего 3х3 метра) тем не менее, он отличается наибольшей стабильностью и совместимостью с языком PostScript, на который ориентируются практически все издательско-полиграфические приложения.

CDR (CorelDRAW Document) - основной рабочий формат популярного пакета CorelDRAW, являющимся неоспоримым лидером в классе векторных графических редакторов на платформе РС. Имея сравнительно невысокую устойчивость и проблемы с совместимостью файлов разных версий формата, тем не менее, формат CDR можно без натяжек назвать профессиональным. В файлах этих версий применяется раздельная компрессия для векторных и растровых изображений, могут внедряться шрифты, файлы CDR имеют огромное рабочее поле 45х45 метров, поддерживается многостраничность.

WMF (Windows Metafile) - еще один формат Windows, на сей раз векторный. Понимается практически всеми программами Windows, так или иначе связанными с векторной графикой. Однако, несмотря на кажущуюся простоту и универсальность, пользоваться форматом WMF стоит только в крайних случаях, поскольку он не может сохранять некоторые параметры, которые могут быть присвоены объектам в различных векторных редакторах, не воспринимается Macintosh-ами, и, самое главное, способен исказить цветовую схему изображения.

PDF (Portable Document Format) - первоначально проектировался как компактный формат электронной документации, но в последнее время все больше используется для передачи по сетям графических изображений и смешанных документов, содержащих как текст, так и графику. Формат PDF является в полной мере платформонезависимым форматом, в текстовой части которого возможно использование множества шрифтов (которые содержатся непосредственно в документе, поэтому документ будет выглядеть так, как задумал его автор, на любом компьютере) и гипертекстовых ссылок, а также графические иллюстрации любого типа (векторные или растровые). Для достижения минимального размера PDF-файла используется компрессия, причем каждый вид объектов сжимается по наиболее выгодному для него алгоритму. Просматривать документы в формате PDF и распечатывать их на принтере можно с помощью утилиты Acrobat Reader, распространяемой компанией Adobe бесплатно.

Особый класс программ для работы с любыми видами изображений представляютпрограммы-просмотрщики. Они позволяют просматривать графические файлы различных форматов, создавать фотоальбомы на жестком диске, перемещать, переименовывать, изменять размеры, а также конвертировать из одного формата в другой изображения. Лидером в данной области является программа ACDSee.

№7 Фрактальные графики

Последней из рассматриваемых видов компьютерной графики - это фрактальная графика. Фрактальная графика является на сегодняшний день одним из самых быстро развивающихся перспективных видовкомпьютерной графики. 

Математической основой фрактальной графики является фрактальная геометрия. Здесь в основу метода построения изображений положен принцип наследования от, так называемых, «родителей» геометрических свойств объектов-наследников. 

Понятия фрактал, фрактальная геометрия и фрактальная графика, появившиеся в конце 70-х, сегодня прочно вошли в обиход математиков и компьютерных художников. Слово фрактал образовано от латинскогоfractus и в переводе означает «состоящий из фрагментов». Оно было предложено математиком Бенуа Мандель-Бротом в 1975 году для обозначения нерегулярных, но самоподобных структур, которыми он занимался. 

Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому. Одним из основных свойств фракталов является самоподобие. Объект называют самоподобным, когда увеличенные части объекта походят на сам объект и друг на друга. Перефразируя это определение, можно сказать, что в простейшем случае небольшая часть фрактала содержит информацию обо всем фрактале. 

В центре фрактальной фигуры находится её простейший элемент — равносторонний треугольник, который получил название «фрактальный». Затем, на среднем отрезке сторон строятся равносторонние треугольники со стороной, равной (1/3a) от стороны исходного фрактального треугольника. В свою очередь, на средних отрезках сторон полученных треугольников, являющихся объектами-наследниками первого поколения, выстраиваются треугольники-наследники второго поколения со стороной (1/9а) от стороны исходного треугольника. 

Таким образом, мелкие элементы фрактального объекта повторяют свойства всего объекта. Полученный объект носит название «фрактальной фигуры». Процесс наследования можно продолжать до бесконечности. Таким образом, можно описать и такой графический элемент, как прямую. 

Изменяя и комбинирую окраску фрактальных фигур можно моделировать образы живой и неживой природы (например, ветви дерева или снежинки), а также, составлять из полученных фигур «фрактальную композицию». Фрактальная графика, также как векторная и трёхмерная, является вычисляемой. Её главное отличие в том, что изображение строится по уравнению или системе уравнений. Поэтому в памяти компьютера для выполнения всех вычислений, ничего кроме формулы хранить не требуется. 

Только изменив коэффициенты уравнения, можно получить совершенно другое изображение. Эта идея нашла использование в компьютерной графике благодаря компактности математического аппарата, необходимого для ее реализации. Так, с помощью нескольких математических коэффициентов можно задать линии и поверхности очень сложной формы.

Итак, базовым понятием для фрактальной компьютерной графики являются «Фрактальный треугольник». Затем идет «Фрактальная фигура», «Фрактальный объект»; «Фрактальная прямая»;«Фрактальная композиция»; «Объект-родитель» и «Объект наследник». Следует обратить Ваше внимание на то, что фрактальная компьютерная графика, как вид компьютерной графики двадцать первого века получила широкое распространение не так давно. 

Её возможности трудно переоценить. Фрактальная компьютерная графика позволяет создавать абстрактные композиции, где можно реализовать такие композиционные приёмы как, горизонтали и вертикали, диагональные направления, симметрию и асимметрию и др. Сегодня немногие компьютерщики в нашей стране и за рубежом знают фрактальную графику. С чем можно сравнить фрактальное изображение? Ну, например, со сложной структурой кристалла, со снежинкой, элементы которой выстраивается в одну сложную структуру. Это свойство фрактального объекта может быть удачно использовано при составлении декоративной композиции или для создания орнамента. Сегодня разработаны алгоритмы синтеза коэффициентов фрактала, позволяющего воспроизвести копию любой картинки сколь угодно близкой к исходному оригиналу. 

С точки зрения машинной графики фрактальная геометрия незаменима при генерации искусственных облаков, гор, поверхности моря. Фактически благодаря фрактальной графике найден способ эффективной реализации сложных неевклидовых объектов, образы которых весьма похожи на природные.Геометрические фракталы на экране компьютера — это узоры, построенные самим компьютером по заданной программе. Помимо фрактальной живописи существуют фрактальная анимация и фрактальная музыка. 

Создатель фракталов — это художник, скульптор, фотограф, изобретатель и ученый в одном лице. Вы сами задаете форму рисунка математической формулой, исследуете сходимость процесса, варьируя его параметры, выбираете вид изображения и палитру цветов, то есть творите рисунок «с нуля». В этом одно из отличий фрактальных графических редакторов (и в частности — Painter) от прочих графических программ.

Например, в Adobe Photoshop изображение, как правило, «с нуля» не создается, а только обрабатывается. Другой самобытной особенностью фрактального графического редактора Painter (как и прочих фрактальных программ, например Art Dabbler) является то, что реальный художник, работающий без компьютера, никогда не достигнет с помощью кисти, карандаша и пера тех возможностей, которые заложены в Painter.

№8 Понятие цветовых моделей. Глубина цвета.

Понятие цветовой модели

Мир, окружающий человека, воспринимается по большей части цветным. Цвет имеет не только информационную, но и эмоциональную составляю­щую. Человеческий глаз — очень тонкий инструмент, но, к сожалению, вос­приятие цвета субъективно. Очень трудно передать другому человеку свое ощущение цвета.

Вместе с тем для многих отраслей производства, в том числе для полигра­фии и компьютерных технологий, необходимы более объективные способы описания и обработки цвета.

Для описания цвета придуманы различные цветовые модели. Наиболее используемые делятся на три больших класса: аппаратно-зависимые (описывающие цвет применительно к конкретному устройству цветовоспроизведения, например, монитору, — RGB, CMYK), аппаратно-независимые (для однозначного описания информации о цвете — XYZ, Lab) и психологические (основывающиеся на особенностях человеческого восприятия — HSB, HSV, HSL) (рис. 1).

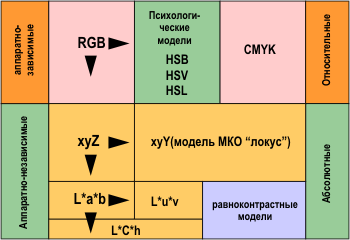
Рис. 1. Иерархия цветовых моделей

В графических редакторах для присвоения цветовых параметров объектам можно использовать несколько цветовых моделей в зависимости от задачи. Эти модели различаются по принципам описания единого цветового про­странства, существующего в объективном мире.

Глубина цвета

Глубиной цвета называют количество градаций одного цвета, которое то или иное устройство способно записать или воспроизвести. Именно глубина цвета определяет, насколько плавными получаются тональные переходы на наших фотографиях. Поскольку мы говорим о цифровых изображениях, то кодируются они в виде нулей (черный цвет) и единиц (белый цвет). Хранятся эти нули и единицы в ячейках памяти, которые называются байтами. Каждый байт состоит из восьми бит. Глубину цвета обозначают в битах.

Индексированные цвета и палитры

Возможные варианты представления цветовых палитр:

4-битное изображение

• 1-битный цвет (2¹ = 2 цвета) бинарный цвет, чаще всего представляется чёрным и белым цветами (или черный и зелёный)

• 2-битный цвет (2² = 4 цвета) CGA, градации серого цвета NeXTstation

• 3-битный цвет (2³ = 8 цветов) Множество устаревших персональных компьютеров с TV-выходом

• 4-битный цвет (2⁴ = 16 цветов) известен как EGA и в меньшей степени как VGA-стандарт с высоким разрешением

• 5-битный цвет (2⁵ = 32 цвета) Original Amiga chipset

• 6-битный цвет (2⁶ = 64 цвета) Original Amiga chipset

• 8-битный цвет (2⁸ = 256 цветов) Устаревшие Unix-рабочие станции, VGA низкого разрешения, Super VGA, AGA

• 12-битный цвет (2¹² = 4,096 цветов) некоторые Silicon Graphics-системы, цвет NeXTstation-систем, и Amiga-систем HAM-режима.

8-битное изображение

[Править]«Реальные» цвета

С увеличением количества бит в представлении цвета, количество отображаемых цветов стало становиться непрактично-большим для цветовых палитр (20-битная глубина цвета требует больше памяти для сохранения цветовой палитры, чем памяти для сохранения самих пикселейизображения). При большой глубине цвета на практике обычно кодируют яркости красной, зелёной и синей составляющих — такое кодирование обычно называют RGB-моделью.

[Править]8-битный «реальный» цвет

Сильно ограниченная, однако «реальная» цветовая схема, в которой 3 бита (8 возможных значений) для красной (R) и зелёной (G) составляющих, и два оставшихся бита на пиксель для кодирования синей (B) составляющей (4 возможных значения), позволяют представить 256 (8 × 8 × 4) различных цвета. Нормальный человеческий глаз менее чувствителен к синей составляющей, чем к красной и зелёной, поэтому синяя составляющая представляется одним битом меньше. Такая схема использовалась в MSX2-серии компьютеров в 1990-х.

Не следует путать такую схему с 8bpp индексным цветом, который может быть представлен выбором различных цветовых палитр.

[Править]12-битный «реальный» цвет

12-битный «реальный» цвет кодируется 4 битами (16 возможных значений) для каждой R, G и B-составляющих, что позволяет представить 4096 (16×16×16) различных цветов. Такая глубина цвета иногда используется в простых устройствах с цветными дисплеями (например, в мобильных телефонах).

[Править]HighColor

Highcolor или HiColor разработан для представления оттенков «реальной жизни», то есть наиболее удобно воспринимаемый человеческим глазом. Такой цвет кодируется 15 или 16 битами:

• 15-битный цвет использует 5 бит для представления красной составляющей, 5 для зелёной и 5 для синей, то есть 2⁵ = 32 возможных значения каждого цвета, которые дают 32768 (32×32×32) объединённых цвета.

• 16-битный цвет использует 5 бит для представления красной составляющей, 5 для синей, но (так как человеческий глаз более чувствителен при восприятии зелёной составляющей) 6 бит для представления зелёной, соответственно 64 возможных значения. Таким образом получаются 65536 (32×64×32) цвета. 16-bit цвет упоминается как «тысячи цветов» («thousands of colors») в системах Macintosh.