Методические указания к решению заданий контрольной работы №2

ПРИМЕР 1. Дано комплексное число z = – 4  – 4∙i.Требуется:

1) Изобразить число z в виде радиус-вектора на комплексной плоскости;

2) Записать число z в тригонометрической форме;

3) Найти все значения .

Решение. 1) Комплексным числом называется число z = x + i∙y, где х и у – действительные числа, а i – мнимая единица, i² = – 1.

х = Rez называется действительной частью комплексного числа, а у = Imz – мнимой частью комплексного числа.

Запись числа в виде z = x + i∙y называется алгебраической формой комплексного числа.

Всякое комплексное число z = x + i∙y можно изобразить точкой М(х; у) плоскости Оху такой, что х = Rez, у = Imz. Плоскость, на которой изображается комплексное число, называется комплексной плоскостью, при этом ось абсцисс называют действительной осью, а ось ординат – мнимой осью.

Комплексное число изображают также на комплексной плоскости с помощью радиус-вектора =   = (х; у).

В нашем случае z = – 4  – 4∙i. Имеем х = Re z = – 4 , у = Im z = – 4.

Изобразим это число на комплексной плоскости в виде радиус-вектора. Для этого построим точку и соединим ее с началом координат. Тогда радиус-вектор изображает число z на комплексной плоскости (рисунок 1).

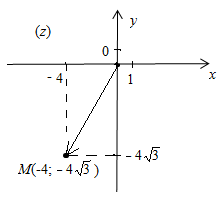
Рисунок 1

2) Запишем число в тригонометрической форме

,

где – модуль комплексного числа, – аргумент комплексного числа .

Аргумент комплексного числа z ≠ 0 – величина многозначная и определяется с точностью до слагаемого 2πk (k = 0,– 1, 1, – 2, 2 …): Argz = аrgz + 2πk, где аrgz – главное значение аргумента, заключенное в промежутке (– π; π], то есть (иногда в качестве главного значения аргумента берут величину, принадлежащую промежутку [0; 2π)). Аргумент φ определяется из формулы . Так как , то получаем, что

arg z = 

Тогда модуль комплексного числа z = – 4  – 4∙i:

 =   =   =   =   = 8,

а так как точка М находится в III четверти, то аргумент

.

Тогда – тригонометрическая форма комплексного числа z.

3) Для нахождения воспользуемся формулой

w_k =   =  (cos  + isin ), где k = 0, 1, 2, …, п – 1.

В нашем случае имеем п = 3 и

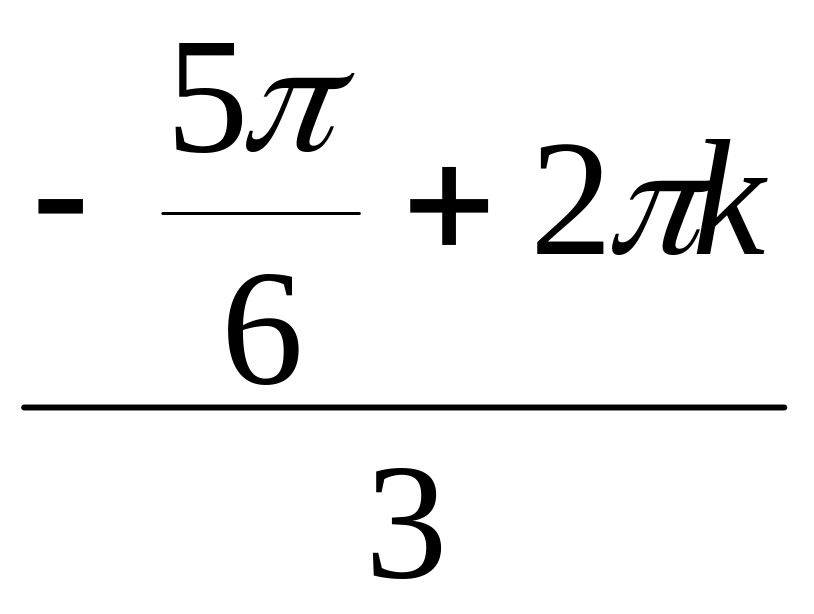w_k =   =  (cos  + isin ), где k = 0, 1, 2.

Придавая k последовательно значения 0, 1, 2, находим все три значения корней:

w₀ =  (cos( ) + isin( )) ≈ 2·(0,643 – 0,766i) = 1,286 – 1,532i,

w₁ =  (cos  + isin ) ≈ 2·( 0,342 + 0,94i) = 0,684 + 1,88i,

w₂ =  (cos  + isin ) =  (– cos  – isin ) ≈ 2·(– 0,985 – 0,174i) = 

= – 1,97 – 0,348i.

ПРИМЕР 2. а) Найти неопределенный интеграл .

Решение

I₁ + I₂.

I₁ =   = 5∙  = [так как ] = 

= 5∙ ∙tg2x + C;

I₂ =   =   = 

=   =  ∙  =  t² + C = 

Таким образом,

 = 

б) Найти неопределенный интеграл .

Решение. Найдём данный интеграл, используя формулу интегрирования по частям:

.

= 

в) Вычислить определенный интеграл .

Решение

 =  =

 =  =

ПРИМЕР 3. Изобразить фигуру, ограниченную указанными линиями:

у = – х, у = 2х – х²

и вычислить ее площадь.

Решение. Нарисуем чертеж фигуры, ограниченной линиями:

у = – х, у = 2х – х².

Методом выделения полных квадратов преобразуем уравнение параболы у = 2х – х²:

у = – (х² – 2х), у = – (х² – 2х + 1 – 1), у = – [(х – 1)² – 1],

у = – (х – 1)² + 1 или .

Из уравнения видно, что вершина параболы находится в точке (1;1), а ее ветви направлены вниз.

Прямая у = – х – это биссектриса второго и четвертого координатных углов (рисунок 2).

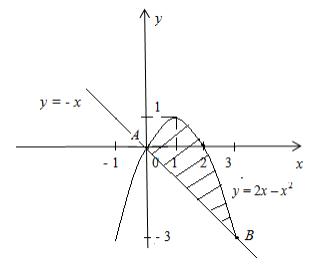
Рисунок 2

Определим абсциссы точек А и В – точек пересечения параболы и прямой. Для этого решим систему уравнений:

Получим: х_А = 0, х_В = 3.

Тогда по формуле вычислим искомую площадь. Для нашего случая

ПРИМЕР 4. а) Найти общий интеграл дифференциального уравнения первого порядка

2х²у′ = х²+ у²

Решение. Так как функции 2х² и х²+у² – однородные функции второго измерения, то данное уравнение – однородное дифференциальное уравнение первого порядка. Такие дифференциальные уравнения решаем с помощью подстановки у = ux, где и = и(х) – новая неизвестная функция, подлежащая определению. Тогда y′ = u + xu′ и

2х²(u + xu′) = x²+ (ux)²,

2х²(u + xu′) = x²(1 + u²).

Предполагая, что х не равно нулю, разделим обе части уравнения на х².

Далее преобразуем это уравнение:

,

2хdx = (1 + u² – 2u)dx

 =  .

Это уравнение с разделяющимися переменными. Разделим переменные и последовательно находим:

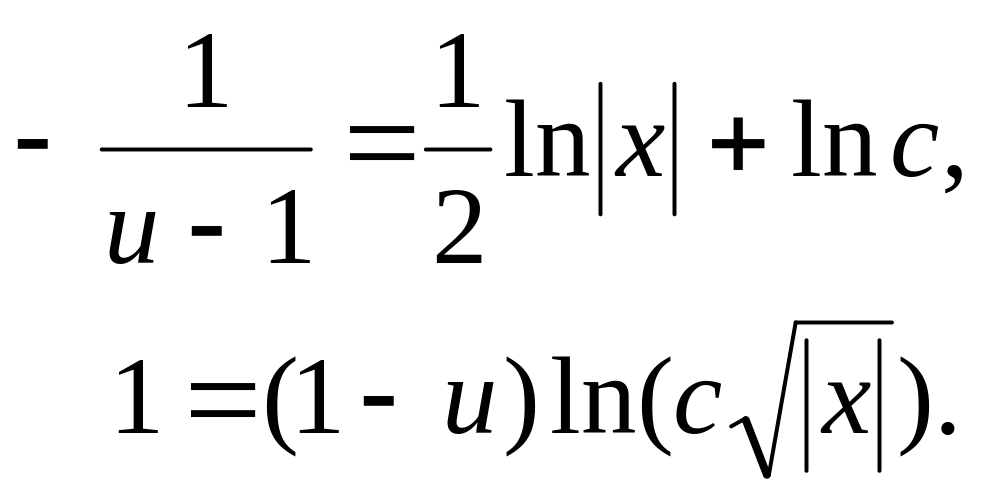
В последнее выражение для u подставим значение . Получим общий интеграл:

.

б) Найти общее решение дифференциального уравнения второго порядка , допускающего понижение порядка.

Решение. Данное уравнение относится к уравнениям вида , не содержащим неизвестную функцию . Понизим его порядок с помощью подстановки у′ = р, где – новая неизвестная функция. Тогда . Подставим в заданное уравнение вместо у′ и у′′ их выражения, получим:

. (1)

Это линейное дифференциальное уравнение первого порядка относительно функции . Решим это уравнение с помощью подстановки Бернулли , где U =  и V =  – новые неизвестные функции. Тогда .

Подставим выражения для и в уравнение (1), получим:

.

Сгруппируем члены последнего уравнения и приведем его к виду:

. (2)

Так как произведение UV должно удовлетворять исходному уравнению, и одну из неизвестных функций, например V, можно выбрать произвольно, то выберем в качестве любое частное решение V = V(х) уравнения:

V′ +  V = 0.

Тогда

или

. (3)

Дифференциальное уравнение (3) – дифференциальное уравнение первого порядка с разделяющимися переменными. Разделим переменные и проинтегрируем его:

, + lnC.

Полагая С = 1, получим частное решение в виде

.

Подставим в уравнение (2). Получим:

или ,

, .

Тогда

или

.

Разделим переменные в полученном уравнении и проинтегрируем его:

.

Найдем общее решение данного уравнения

.

в) Найти частное решение дифференциального уравнения , удовлетворяющее начальным данным: у(0) = 1, у′(0) = 0.

Решение. Согласно структуре общего решения линейного неоднородного дифференциального уравнения оно имеет вид

,

где – общее решение соответствующего линейного однородного уравнения, а – некоторое частное решение исходного линейного неоднородного уравнения.

Найдем общее решение однородного уравнения методом Эйлера. В уравнении заменим . Тогда его характеристическое уравнение

имеет два различных вещественных корня:

.

Общее решение линейного однородного дифференциального уравнения имеет вид

.

Найдем частное решение исходного линейного неоднородного дифференциального уравнения со специальной правой частью методом неопределенных коэффициентов.

Правая часть уравнения – функция – имеет специальный вид, что позволяет установить вид частного решения. Частное решение для такой правой части найдем в виде , где по условию ;  – число корней характеристического уравнения, совпадающих с числом . Так как один из корней характеристического уравнения и совпадает с числом , то и частное решение найдем в виде

.

Подставим предполагаемое решение и его производные

;

в заданное неоднородное дифференциальное уравнение:

Разделим обе части уравнения на и приравняем коэффициенты при одинаковых степенях в левой и правой частях соответственно.

Получим

,

,

,

откуда , .

Тогда и общее решение исходного неоднородного дифференциального уравнения имеет вид

.

Выделим из полученного общего решения исходного неоднородного дифференциального уравнения частное решение, удовлетворяющее начальным условиям . Для этого подставим начальные условия в систему

Будем иметь

Решая систему, найдем . Тогда искомым частным решением является функция

.

ПРИМЕР 5. Найти радиус сходимости и область сходимости степенного ряда .

Решение. Для определения радиуса сходимости данного степенного ряда воспользуемся формулой .

Так как для нашего ряда и , то

Итак, радиус сходимости ряда . Определим интервал сходимости данного степенного ряда:

 < 5   – 5< x +2 <5   – 7< x <3.

Таким образом, – интервал сходимости исследуемого степенного ряда. Исследуем сходимость ряда на концах интервала сходимости.

Пусть . Подставим в заданный степенной ряд.

.

Мы получили знакочередующийся числовой ряд, который сходится, так как выполняются условия теоремы Лейбница:

1) а_п > а_п + 1, так как и

2) .

Следовательно, принадлежит области сходимости степенного ряда.

Пусть . Подставим в заданный степенной ряд и получим числовой ряд

.

Этот ряд с положительными членами, общий член которого а_п =  . Для определения его сходимости применим предельный признак сравнения. Сравним данный ряд с гармоническим рядом , который расходится.

Получим

.

В соответствии с предельным признаком сравнения оба ряда ведут себя одинаково и, следовательно, исходный ряд расходится. Значит, не принадлежит области сходимости степенного ряда.

Итак, областью сходимости данного степенного ряда является промежуток .