
- •35. Корені многочленів. Теорема Безу. Метод Горнера
- •36 Основна теорема алгебри
- •37. Раціональні дроби
- •38.Аксіоматичне визначення векторного простору
- •40.Підпростори векторного простору
- •41.Афінний простір...
- •42.Ранг матриці.
- •43.Підпр, утвор ровязк однор слр
- •44 Неоднор системи лінійних рівнянь. Теорема Кронекера-Капеллі
- •45.Лп та їх матриці. Дії над лп. Обернене лп.
- •46.Матриці лінійного перетвор. Подібні матриці.
- •47.Характеристичний многочл, власні числа і власні вектори лп
- •48. Означ евклід прост. Ортог вектори. Ортогоналізація Гр-Шмі.
- •49.Ортонормовані базиси і ортогональні матриці.
- •50.Ортогональні перетворення.
- •51 Означення квадратичних форм(кф). Основні ознаки додатної визначеності.
- •52 Зведення кф до канонічного вигляду
- •53) Поняття множини. Рівність множин.
- •54) Операції над множинами.
- •55) Означення функції. Види відображень.
- •56. Складена, обернена функція.
- •57. Параметричне та неявне відображення.
- •58. Аксіоми множин дійсних чисел
- •59. Розширення множини дійсних чисел
- •60. Основні характеристики дійсного числа.
- •61. Обмежені та необмежені числові множини.
- •62. Верхня та нижня межа множини.
- •63 Принцип Архімеда.
- •64. Принцип вкладених відрізків
- •65) Еквівалентність множин та поняття потужності
- •66) Зчисленна потужність
- •67) Континуальна потужність
52 Зведення кф до канонічного вигляду
Рангом КФ наз. ранг її матриці А. При зміні змінних х=Су КФ переходить у КФ від нових змінних у1,у2,…,уn . Перетворення змінних х=Су назив. не виродженим, якщо матриця С є не виродженою. Канонічною виглядом КФ назив. представлення її як алгебраїчні сума квадратів
 .(1)
.(1)
f(y)=∑nj=1 λiyi2, де λi≠0, к-ть ненульових доданків = рангу КФ. Теорема Для того, щоб симетр.А можна подати у вигляді А= QΛQT, де Q – ортогональна, Λ – діагональна, необхідно і достатньо щоб Q складал. З ортонормованих власних векторів А, а Λ мала діагональні елементи відповідні власні значення А.
Теорема Будь-яку КФ ортогоню перетворень можна звести до канонічного вигляду.
Доведення:
Нехай Q – ортогональна матриця, що складена з ортонормованих власних векторів А. QT = Q-1 х= Qу, у= QT х. розглянемо КФ: f= хтАх=хт QΛQTх=ут Λу=∑ni=1 λiyi2.
Теорема (закон інерції КФ)
К-ть доданків з додатніми (від’ємними) коефіцієнтами в нормальному вигляді КФ не залежить від способу зведення КФ до цього вигляду.
Зауважимо, що звести квадратичну форму до канонічного вигляду можна і так званим методом Лагранжа або методом виділення повних квадратів.
Нехай
квадратична форма зведена до канонічного
вигляду (1), причому відмінні від нуля
канонічні коефіцієнти занумеровані
так, що
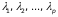 є додатними, а
є додатними, а
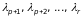 - від’ємними. За допомогою невиродженого
лінійного перетворення змінних
- від’ємними. За допомогою невиродженого
лінійного перетворення змінних
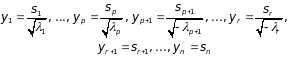
Квадратичну форму можна звести до вигляду:
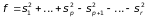 ,
(
,
(
який називається нормальним виглядом квадратичної форми.
53) Поняття множини. Рівність множин.
Множина- первинне визначення математичного аналізу. Поняття множини вважається первісним і інтуїтивним. Множина задається правилом або ознакою відповідно до якого визнач. Чи належить деякий елемент множ. чи ні.
А={а}, де А скл або з множ. склад. з 1 елемента а малого. Множину можна задавати за допомогою переліку її елементів А={а ,в, с...}
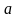 є
А-
елемент а належить множині А.
є
А-
елемент а належить множині А.
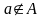 -
а не належить множині А
-
а не належить множині А
Елементи множини А, що мають власн. Р
А1={а
єА
 (а має вл. Р)}
(а має вл. Р)}
А1 ={а: (а є А) (а має вл. Р)}
множина В наз. підмножиною множини А ,якщо всі елементи множини В є елементами множини А.
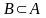 В
підмножина А
В
підмножина А
Позначимо
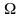 - універсальна множина та будемо
розглядати всі інші множини як підмножини
універсальної.
- універсальна множина та будемо
розглядати всі інші множини як підмножини
універсальної.
Порожньою множиною наз. множина, що не містить жодного елемента.
 Множина
А і В наз рівними, якщо вони містять одні
й ті самі елементи
А=В (А
В)
(В
А)
Множина
А і В наз рівними, якщо вони містять одні
й ті самі елементи
А=В (А
В)
(В
А)
Позначення
Множина натуральних чисел : N= {1,2,3…}
Z0- множина додатніх цілих чисел Z0- {0,1,2,3…}
Z-
{0,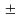 1,
2…}
– цілих чисел
1,
2…}
– цілих чисел
Q=
{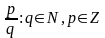 }
Q-
раціональні
}
Q-
раціональні
І- нескінченні неперіодичні дроби. R – дійсні. С- комплексні
Множина N ма’є такі влас. (аксіоми):
якщо n є N
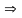 (
n +1)
є
N
(
n +1)
є
N1 є М (деяка множина), (n є М ( n +1) є М ) N М- аксіома індукції
Метод мат індукції:нехай задано твердження А1.А2….Аn та доведені леми паскаля
Лема 1:А1 істинне,Аn-істинне.
Лема2:з істинності твердження An вопливає істинність твердження An+1.
Тоді всі твердження Ai,i=1,+∞ - істинні.
