35. Корені многочленів. Теорема Безу. Метод Горнера
Нулем, або коренем многочлена f(x) назив. Число сєС таке,що f(c)=0
Теорема Безу
При діленні многочлена f(x) на двочлен (x-c) одержується остача f(c)
Доведення
f(x)=(x-c)q(x)+r, r многочлен 0-го степеня,(rєC).
x=c
f(c)=(c-c)q(c )+ r=r
Наслідок. Якщо c є коренем f(x), то f(x) ділиться на (x-c), тобто
(1)f(x)=(x-c)q(x), f(x)- n степеня ,q(x) –(n-1) степеня.
Для ділення f(x) на (x-c) зручно використ. Схему Горнера
Нехай f(x)=a0xn+a1xn-1+…+an
q(x)=b0xn-1+b1xn-2+…+bn-1
Підставимо f(x) і g(x) в (1) та прирівняємо коефіцієнти при однакових коренях x
xn
a0=b0b0=a0
xn-1 a1=b1-cb0b1=cb0+a1
xn-2
…
x0 b0=a0 bk=cbk-1+ak k=1,n-1
r=cbn-1+an(якщо є остача)
Корінь
c
многочлена
f(x)
назив
коренем кратності k,
якщо
f(x)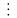
(x-c)k,
але
не ділиться на (x-c)k+1
f(x)=(x-c)kq(x)
36 Основна теорема алгебри
Будь-який многочлен з б-якими числовими коеф, степінь якого не менше одиниці має хоча б один корінь—у заг випадку комплексний.
Наслідок1: б-який мнч n-го степеня розкладається на n лінійних множників та множник рівний старшому коеф .
f(x)=а0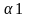(x-
)(x-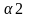
)*…*(x-
)
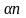Наслідок2 многочлен n-го степеня не може мати більше n коренів
Наслідок3 f(x) (cтепеня більше один) має рівно n коренів, якщо кожен корінь взятий стільки разів, скільки його кратність, тобто
f(x)=a0
(x-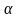
1)
(x-
2)
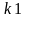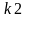*…*(x-
n)
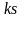ki
є N.k1+k2+…+ks=n;
Наслідок 4Якщо многочлен тотожно рівний нулю, то всі його коеф рівні нулю
Насл
5
Якщо f(x)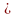
g(x)то
коеф f(x)
відповід рівні коеф g(x)
ai=bi,
i=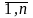
f(x)-g(x)
0
a0-b0,
a0=b0;
і тд
Розглянемо f(x) з дійсними коеф.
Теорема Якщо мнч f(x) з дійсними коеф має корінь (a+ib), то він має корінь (a-ib)
Отже в розкладі f(x) на множники зустрічаються такі множники (x-a-ib), (x-a+ib)
(x-a-ib)(x-a+ib)=(x-a)(x-a)+b*b=x*x+px+q; D<0;
Теорема Будь-який мнч можна ідентифікувати у вигляді:
f(x)=a0
(x-
1)
(x-
2)
*…*(x-
n)
(x*x+p1x+q1)
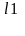(x*x+p2x+q2)
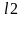*…*(x*x+prx+qr)
)
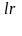де αi, pi, qi, a0 єR
ki, Lj єN
k1+k2+…+ks+2l1+2l2+…+2lr=n;
37. Раціональні дроби
Дробово-раціональною ф-кцією (рац дробом) наз частка двох мнч
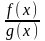g(x)
не дор
нулю
Якщо степінь знаменника більше(менше) ніж степінь чисельника, то дріб—правильний(непр)
Дріб наз нескоротним, якщо чис і знам –взаємнопрості
Теорема Б-який рац дріб можна однозначно представити у вигляді суми мнч і правильного дробу(наслідок ділення з остачею)
Доведення :
f(x)=g(x)*q(x)+r(x);
=q(x)+
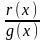степіні
ер менше за степінь дж-за властивістю
дільника та остачі
Правильний дріб наз елементарним, якщо знаменник—степінь незвідного мнч
Тобто, це дроби виду
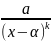або
Теорема Б-який рац прав дріб можна однозначно представити у вигляді суми елементарних дробів
38.Аксіоматичне визначення векторного простору
Множина R-векторний простір, якщо для елем цієї множини виконуються вимоги:
1)кожній
парі
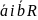відповідає
вектор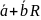
,
який є сумою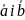
;
2)кожній
парі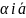
(α-число)
відповід вектор
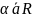(добуток
вектора
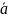і числа
α)
3)операції
+ і ∙
вектора
на число задовольняє аксіоми(
-вектори,
α,
β-числа):
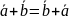
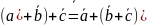
існує
вектор
,
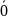що
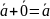
-для
кожного
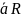існує
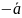(протилежний)
і а+(-а)=0
-1∙а=а
-α(βа)=(αβ)а
-(α+β)а=αа+βа
-α(а+b)=αa+αb
Різниця векторів a і b назив вектор a-b що =сумі векторів a і (-b), тобто a-b=a+(-b)
Нульовим вектором прост Rn є вектор 0=(0,0,…,0)т, а протилежним до вектора а=(а1,а2,…,аен)т є вектор –а=(-а1,-а2,…,-аен)т
Лін
комб векторів
а1,а2,…,аен
– вектор
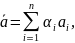де
α1, α2,…,αен – числа.
ЛЗ
вектори:
якщо α1, α2,…,αен не=0 одночасно і
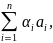=0(1)
ЛН: якщо (1) можливо лише коли α1=α2=…=αен=0
Теорема: Щоб вектори а1,а2,…,аn були ЛЗ необх і достатньо щоб принаймні 1 був лін комб інших.
Два ЛЗ вектори – колінеарні.
39.
Вимірн і базис вект пр. Перет коорд при
пер до нового базису.
Максим
к-сть лін незал векторів ВП назив його
розмірн
і познач dim
R=n,
тобто R
– n-вимірний
простір. Якщо ( а1 а2 ……..аn)
– лін-незал с-ма n
– вимірного простору, то додав будь-якого
вектора до даної с-ми перетворює її у
лін-залеж с-му. Отже, будь-який ( n+1
) – вектор є лін комбінацією векторів
а1 а2..аn.
Б-яка лін-незал с-ма, що скл з незалежних n-векторів назив базисом n-вимір прост.
Розкладом н-вим вектора за базис е1, е2,….ен назив представленням:
а
=
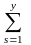αi
еi,
де αi
належить R,
аі назив коорд вектора а віднос базиса
е1, е2, …., ен.
Теорема : Коорд вектора віднос деякого базиса визнач однозначно.
Введ поняття розкладу вектора за базисом дозвол перевести операц над векторами на мову операцій над коорд цих векторів. Отже, загал н-вимірний простір улаштований так само, як арифметичний простір м*н.
Нехай е1, е2,….,ен – старий базис, а е1’, е2’, …., ен’ – новий базис. Нехай відомі коорд векторів нового базису відносно старого.
(1)
ej’=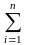
αij
ei
, де αij
- координати розкладу, j=1,n(1)
q11 q12 …..q1n
( е1’, е2’, …., ен’)=( е1, е2,….,ен)* ( q21 q22 … q2n)
……………………
qn1 qn2 …..qnn
( е1’, е2’, …., ен’)T=( е1, е2,….,ен)T *Q (2), Q- матриця переходу від старого базису до нового.
(α1,α2,…,αен)т
і (α1',α2',…,αен')т-матриці-стовпці
корд вект
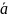у стар і нов. базисах, тоді а=
;
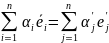(1)+(2)→
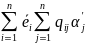
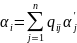i=1,n
або
(α1',α2',…,αn')т=Q-1(α1,α2,…,αn)-коорд вект а в нов. баз через старий