В соответствии с (6.344), (6.345) наблюдатель описывается уравнениями:

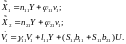
На основе уравнений (6.346) и (6.347) запишем

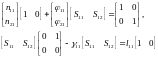
или

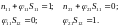
Откуда

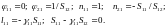
В результате запишем

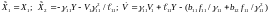
при .

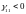30.. Адаптивные системы упр-я. Классиф-я. Синтез адапт-й системы с эталонной моделью на основе подстройки коэффициентов уравнения переменных состояния.

Рассмотрим объект управления, возмущенное движение которого описывается уравнениями:

;

,

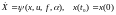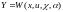где x(t)  nмерный вектор переменных состояния объекта, y(t) rмерный вектор измеряемых (выходных) переменных, f(t), (t)  s и мерные векторы внешних возмущений и помех соответственно, (t)  lмерный вектор неизвестных параметров объекта, u mмерный вектор управления.

Пусть в первом приближении можно воспользоваться линейной нестационарной моделью вида

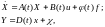
где часть или все элементы матриц A(t), B(t), (t), D(t) являются неопределенными параметрами, из которых можно составить вектор

.

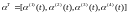Природа неопределенных параметров может быть различной: неточное значение математической модели объекта; неполная информация о программном движении; разброс параметров в пределах технологических допусков; старение элементов объекта.

Объем сведений о параметрах объекта может быть различным:

• неопределенные, ограниченные по модулю параметры

;

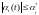• параметры объекта являются случайными функциями времени с известным законом распределения вероятности, но неизвестными параметрами;

• функции 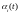заранее известны, однако могут быть измерены в процессе работы объекта.

Обычно параметры объекта изменяются медленнее, чем переменные состояния. Поэтому интервал [t0, t] функционирования объекта можно разделить на подинтервалы, соответствующие постоянству их параметров .

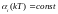Тогда период Т можно назвать интервалом, на котором объект имеет квазистационарные параметры. Это позволяет говорить о k-вариантах модели объекта.

Системы с адаптивной оценкой параметров

Системы данного класса предназначены для восстановления неизвестной характеристики объекта, описываемой конечно-мерным вектором Q вещественных параметров, на основе оценки сигналов системы в реальном масштабе времени. Чтобы получить модель объекта, нет необходимости явно определять параметры. Их можно выбирать на основе косвенных критериев с учетом сигналов объекта управления. Оценка конечномерных параметров модели по информации о состоянии моделируемой системы может быть описана регрессионным вектором сигнала (t). Адаптивная оценка состоит в том, что на основе регрессионного вектора сигнала (t), оценки параметра за прошлое время 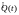и сигнала ошибки e(t) корректируется или заново вычисляется оценка параметра. Сигнал ошибки e(t) вычисляется как разность между сигналом, восстановленным с с помощью , и опорным значением критерия качества, заданным или вычисляемым по измерениям параметров объекта.

Если совокупность внешних сигналов, действующих на систему, обозначить w(t), то полная адаптивная система может быть представлена в виде трех взаимосвязанных подсистем.

Подсистемы регрессии, на вход которой поступают сигналы w(t) и , а на входе формируется сигнал (t) в виде

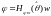. (7.1)

Подсистема обычно включает как объект управления, так и регулятор с замкнутой обратной связью.

Подсистема ошибки, на вход которой поступают сигналы w(t), (t) и , а на выходе образуется сигнал ошибки e(t) для адаптивной коррекции в виде

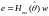. (7.2)

Подсистема адаптации, в которой е и  используются для получения оценок параметра 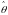в виде

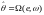. (7.3)

Объединяя перечисленные подсистемы в одну структурную схему, получим систему, приведенную на рис.7.1.

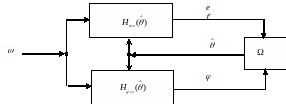
Рис. 7.1 Адаптивная система

Модель адаптивной системы рис. 7.1 имеет вид

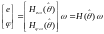, (7.4)

где .

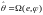Для динамических адаптивных систем важна устойчивость при наличии небольших возмущений объекта, внешних сигналов, начальных условий, операторов, алгоритмов, т.е. необходима локальная устойчивость уравнения (7.4) с помощью линеаризации, которая бы обеспечивала робастность адаптивной системы.