29.. Синтез наблюдателей переменных состояния.

Рассмотрим объект управления, возмущенное движение которого описывается уравнением

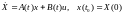, (6.319)

и одним из методов определен оптимальный закон управления

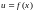. (6.320)

Традиционно существует проблема измерения переменных состояния, что умоляет результат синтеза оптимального закона управления в функции переменных состояния. Доступными измерению являются выходные переменные системы, связанные с переменными состояния соотношением

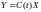. (6.321)

В связи с этим возникает задача наблюдения (восстановления, оценки) вектора x(t) по результатам измерения y(t) на интервале [t0, t].

Обозначим вектор переменных состояния, полученных с помощью какого-либо алгоритма наблюдения через 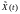. Рассмотрим некоторые алгоритмы наблюдателей переменных состояния.

Наблюдатель полного порядка

Пусть простейший наблюдатель имеет модель

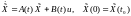. (6.322)

Если бы удалось задать значение 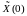равным Х(0), то решение уравнения (6.322) точно совпадало бы с решением (6.319).

Если , то возникает ошибка наблюдения , которая удовлетворяет уравнению

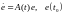(6.323)

Если объект управления асимптотически устойчив, то ошибка наблюдения будет с течением времени уменьшаться

.

Если дополнить уравнение (6.322) составляющей, содержащей измеряемый вектор Y, то такой алгоритм наблюдателя можно записать в общем, виде:

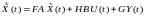. (6.324)

Уравнения для определения матриц F, H, G могут быть получены разными способами.

В простейшем случае пусть система имеет один вход и один выход. Для данного случая можно воспользоваться методом передаточной функции

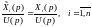. (6.325)

Преобразование Лапласа уравнений (6.319) при нулевых начальных условиях имеет вид

,

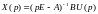где (рЕ  А)-1В есть матричная передаточная функция.

Уравнение наблюдателя (6.324), преобразованное по Лапласу при нулевых начальных условиях имеет вид

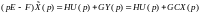
или

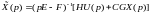. (6.326)

Подставляя в уравнение (6.326) уравнение (6.325), получим

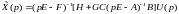. (6.327)

Из условия (6.325) можно записать, что

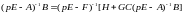. (6.328)

Уравнение (6.328) можно трансформировать к виду

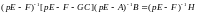
или

.

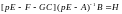Если выбрать

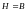и 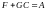, (6.329)

то равенство будет выполняться.

На основании (6.324) и (6.329) представим уравнения наблюдателя состояния в виде

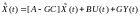. (6.330)

Для определения матрицы G воспользуемся уравнением модели ошибки

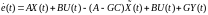(6.331)

или

. (6.332)

Уравнение (14) показывает, что ошибка оценки состояния имеет ту же самую динамику, что и наблюдатель состояния, исходя их характеристического уравнения (12):

. (6.333)

Матрицу G обычно выбирают так, чтобы переходный процесс в наблюдателей закончился быстрее, чем переходный процесс в системе. Эмпирически установлено, что наблюдатель должен обладать быстродействием в 2-4 раза превышающим быстродействие системы. Можно составить характеристическое уравнение

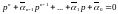, (6.334)

которое соответствует желаемому быстродействию.

Характеристическое уравнение (6.333) имеет вид

.

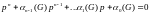Из равенств

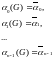(6.335)

можно найти элементы матрицы G .

В матричной форме можно воспользоваться правилами размещения собственных чисел на основе задач модельного управления, когда требуется для выражения

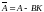(6.336)

найти матрицу К, которая позволила бы иметь матрицу 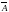с набором желаемых собственных чисел. Для этой цели выполняется преобразование в форме Фробениуса-Кальмана к матрице S со столбцами S1, S2, Sn, строящимися по формулам

(6.337)

где 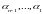коэффициенты характеристического многочлена матрицы А:

.

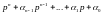Использование матрицы S позволяет записать уравнение (6.336) в форме

(6.338)

где .

Элементы матрицы 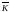вычисляются

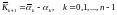(6.339)

и формируют строку 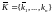. Это вытекает из условия, что произведение и формируют матрицы собственных чисел матриц 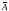и А. Матрица 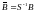состоит из единичных векторов.

Искомая матрица K находится

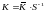. (6.340)

Применяя данный метод для расчета матрицы G наблюдателя можно переписать уравнение (6.336) в виде

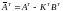. (6.341)

Правая часть уравнения (6.341) подобна на матричное выражение для наблюдателя, из выражения (6.333):

,

что позволяет использовать рассмотренный метод размещения полюсов. Такой же результат можно получить, если использовать подстановку

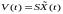. (6.341а)

Тогда уравнение (12) перепишем в виде

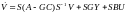(6.342)

или ,

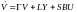где .

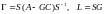Исключая G из последних соотношений, имеем

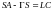. (6.343)

Наблюдатель, описываемый уравнением (6.340), (6.342), (6.343), был получен Люенбергом и поэтому его часто называют наблюдателем Люенбергера.

Обычно некоторые из переменных состояния доступны для измерения и скорее всего непосредственное измерение переменной будет более точным, нежели оценка переменной с помощью наблюдателя. Тогда размерность вектора состояний наблюдателя будет меньше на число измеренных координат (r) и такой наблюдатель называется редуцированным наблюдателем. Он описывается уравнениями

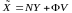; (6.344)

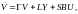(6.345)

где V  вектор состояний пониженного порядка (n – r). Матрицы N и  определяются из уравнения:

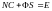. (6.346)

Необходимость этого равенства следует непосредственно из (6.344), если подставить (6.321), (6.341а).

Матрица S находится из уравнения:

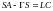, (6.347)

где L – произвольная матрица размера (n  r)  r.

Достаточно распространенный случай в практике Y X1

Пример.

Модель объекта управления