
- •21.. Синтез дискретных компенсационных регуляторов из условия обеспечения желаемого времени регулирования.
- •22.. Синтез дискр-х компенс-х регул-в из условия, обеспеч-х желаемое распол-е полюсов характерист-го уравнения.
- •23. Синтез дискр-х компенс-х регулят-в из условия, обеспеч-х минимизацию дисперсии вых-го сигнала лин-й системы.
- •24.. Элементы инвариационного вычисления и применение их для расчета оптимального управления.
- •Вариационное исчисление в оптимальном управлении
- •25.. Вывод основных соотношений принципа максимума. Проблемы его использования.
- •27.. Акр для линейных непрерывных систем.
- •28.. Акр для линейных дискретных систем.
- •29.. Синтез наблюдателей переменных состояния.
- •В соответствии с (6.344), (6.345) наблюдатель описывается уравнениями:
- •На основе уравнений (6.346) и (6.347) запишем
- •30.. Адаптивные системы упр-я. Классиф-я. Синтез адапт-й системы с эталонной моделью на основе подстройки коэффициентов уравнения переменных состояния.
- •Системы с адаптивной оценкой параметров
- •Адаптивное управление с эталонной моделью в переменных состояния
- •Адаптив-ый р-тор, обеспечив-й настройку коэф-тов уравнения состояния
Вариационное исчисление в оптимальном управлении
В вариац-ном исчисл-и традиционно выд-ся задачи Лагранжа, Майера и Больца.
Задача Лагранжа имеем интегральный критерий оптимизации вида
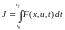 (6.6)
(6.6)
при ограничениях типа системы дифференциальных уравнений
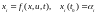 . (6.7)
. (6.7)
В задаче Майера критерий оптимизации имеет вид
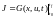 (6.8)
(6.8)
при ограничениях (6.7) и системе конечных условий
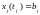 . (6.9)
. (6.9)
Задача Больца включает задачи Лагранжа и Майера.
Рассмотрим задачу Лагранжа в виде минимизации интеграла
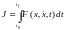 . (6.10)
. (6.10)
Требуется найти функцию x(t), минимизирующую интеграл (6.10).
Пусть
x(t)
функция обеспечивающая минимум, а 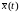
функция близкая к x(t).
Тогда x(t)
и
связаны соотношением
функция близкая к x(t).
Тогда x(t)
и
связаны соотношением
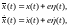 (6.11)
(6.11)
где e малый параметр; (t) произвольная функция, для которой
 . (6.12)
. (6.12)
Заменяя
 и
и
 в интегральном критерии соответственно
на
в интегральном критерии соответственно
на
 и
и
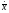 ,
имеем
,
имеем
 .
.
Разлагая подынтегральное выражение в ряд Тейлора и пренебрегая нелинейными составляющими ряда, имеем
 .
.
Интегральный критерий перепишем в виде
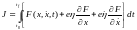 . (6.13)
. (6.13)
Необходимым условием для нахождения экстремума функции J является
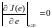 , (6.14)
, (6.14)
откуда следует
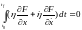 . (6.15)
. (6.15)
Интегрирование по частям второго члена в этом интеграле
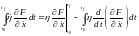 (6.15а)
(6.15а)
приводит к выражению
 . (6.15б)
. (6.15б)
Используя данную зависимость в условии для экстремума, имеем
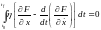 . (6.15в)
. (6.15в)
Откуда следует уравнение Эйлера-Лагранжа
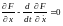 , (6.16)
, (6.16)
решение, которого определяет функцию, доставляющую экстремум J. Данное условие соответствует задаче с закрепленными точками x(t0) и x(tf). Если закреплена точка x(t0), а точка x(tf) лежит на кривой с(t), то уравнение Эйлера-Лагранжа дополняется условием трансверсальности
 . (6.17)
. (6.17)
Рассмотрим примеры использования уравнения Эйлера-Лагранжа. Пусть требуется найти функцию x(t), которая минимизирует функционал
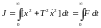 .
.
Находим производные
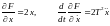 .
.
Подставляя производные в уравнение Эйлера-Лагранжа, имеем уравнение
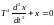 ,
,
решение, которого запишем в виде
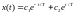 .
.
Если процесс в системе затухает, то при с2 = 0, с1 = х(0) переходный процесс минимизирующий функционал, описывается уравнением x(t) = x0e-t/T.
Изменим критерий качества
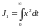 .
.
В этом случае уравнение Эйлера-Лагранжа выражается в алгебраическое уравнение
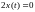 .
.
Если х(0) 0, то обеспечить в системе управления мгновенное устранение отклонения можно лишь при использовании чрезмерных управляющих воздействий.
Вариационные методы применимы, если переменные, обеспечивающие экстремум можно дифференцировать. Управляющие воздействия современных систем могут изменяться, например, по релейному закону, что исключает в этом случае использование методов вариационного исчисления для решения таких задач.
25.. Вывод основных соотношений принципа максимума. Проблемы его использования.
Рассмотрим основные соотн-я данного пр-па на основе реш-я задачи о быстрод-и системы управления. Пусть модель движения объекта управления имеет вид
 (6.18)
(6.18)
и критерий оптимизации равен
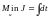 .
(6.19)
.
(6.19)
Объект управления необходимо перевести из начального состояния х0 в фиксированное конечное xf. Предположим, что известна оптимальная траектория движения объекта рис.6.1 и оптимальный закон управления рис. 6.2.


Рис. 6.1 Оптим-я траектория Рис. 6.2 Оптим-й закон упр-ния дв-ния
Пусть при реализации оптимального закона управления в течение короткого времени произошло импульсное отклонение от оптимальной траектории, начиная с момента , а в момент управление возвращается к старой траектории. Траектории, приведенные на рис. 6.1, 6.2 трансформируются (рис. 6.3, 6.4)
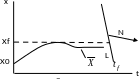

Рис. 6.3 Траектория движения Рис. 6.4 Закон управления системы
системы траектория
Обозначим
неоптим-ю часть траектории дв-я объекта
через
,
а неоптим-й ур-нь упр-ния через
 .
Запишем траектории дв-я неоптим-й и
оптим-ой систем на интервале :
.
Запишем траектории дв-я неоптим-й и
оптим-ой систем на интервале :
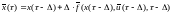 ; (6.20)
; (6.20)
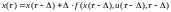 . (6.21)
. (6.21)
Найдем вариацию траектории системы относительно оптимальной траектории
 (6.22)
(6.22)
Пусть равна произвед-ю положит-го целого числа М на малое е. На интервале времени [, tf] движения неоптимальной и оптимальной систем запишем в виде
6.23)
.
Если разложить в ряд Тейлора правую часть уравнения и ограничиться линейными членами разложения, то получим
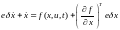 . (6.24)
. (6.24)
В рез-те имеем зав-мость для скорости изменения вариации траектории в виде
 . (6.25)
. (6.25)
Проведем плоскость через N т.о., чтобы ни одна неоптим-я траектория не доходила до данной пл-сти. Местополож-е данной пл-сти х-тся вектором , который соотв-т нормали к данной плоскости в точке N. Отрезок NL соотв-т ( х) вариации неоптимальной траектории относительно оптимальной в момент времени tf.
Между вектором и NL расположен угол, что соответствует негативному значению скалярного произведения этих векторов
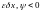 (6.26)
(6.26)
Можно записать составляющие данного неравенства
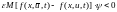 (6.27)
(6.27)
или
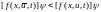 . (6.28)
. (6.28)
Данное нер-во может превр-ся в рав-во при максим-м знач-и произведения
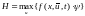 . (6.29)
. (6.29)
Из этого условия и имеем наименование «принципа максимума». Для оценки взаимосвязи координат объекта и вектора примем, что
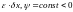 . (6.30)
. (6.30)
Продифференцировав выражение (6.30), имеем
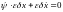 ; (6.31)
; (6.31)
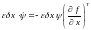 .
.
Откуда следует
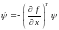 (6.32)
(6.32)
или, используя выражение (6.29), запишем
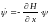 . (6.33)
. (6.33)
Система
дифференциальных уравнений
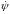 получила наименование сопряженностей
и ее решение возможно совместно с
основной моделью движения объекта:
получила наименование сопряженностей
и ее решение возможно совместно с
основной моделью движения объекта:
 (6.34)
(6.34)
при условии задания начальных или граничных условий на координаты х и . Поскольку вектор введен искусственно, то одна из основных проблем при использовании данного метода заключается в неопределенности начальных или граничных координат . Для критериев качества, отличных от критерия быстродействия, используется процедура замены критерия новой координатой объекта управления. Например, имеем интегральный критерий качества вида
 . (6.35)
. (6.35)
Обозначив J через дополнительную координату xn+1, получим
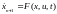 , (6.36)
, (6.36)
которую присоединяем к основной модели динамики движения объекта управления:
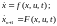 (6.37)
(6.37)
или в виде
 .
.
Относительно расширенной модели формируется функция
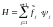 . (6.38)
. (6.38)
Функцию Н часто называют функцией Гамильтона. Если ищется минимум J, то n+1 = 1, а при поиске максимума J1 принимаем n+1 = 1.
Рассмотрим пример задачи о предельном быстродействии динамической системы:
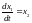 ;
;
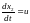
из х1(0) = х2(0) = 0 в заданное x1f и x2f .
Управляющее воздействие ограничено
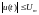 .
.
Составим функцию Гамильтона
 .
.
Сопряженная система имеет вид
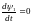 ;
;
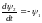 .
.
Интегрируя данную систему, имеем
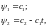
что позволяет записать Н в виде
 .
.
Максимум функции Н
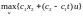
достигается при условии
 .
.
Таким образом, оптимальное значение u(t) соответствует своим предельным значениям. При t = t1 управляющее воздействие меняет знак
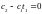 и
и
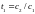 .
.
На интервале времени [0, t1] закон управления определяется
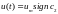 ,
,
что позволяет с учетом нулевых начальных условий х1(0) = х2(0) = 0 записать решения уравнений движения объекта в виде:
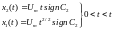 .
.
Для интервала времени [t, tf] имеем

и

С учетом граничных условий для tf находим
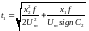 .
.
Поскольку tf t1, то выражение имеет следующий вид:
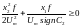 .
.
Рав-во имеет место, когда проц сост-т из 1го инт-ла. Зн-е для t1 опр-ся нер-вом
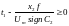 .
.
На основании полученных неравенств можно определить sign C2:
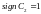 при
при
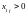 и
и
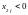 ;
;
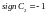 при
при
 и
и
 .
.
Дополнительные исследования знаков sign C2 при x1f > 0, x2f > 0 и
х1f < 0, x2f < 0 позволяют записать следующие неравенства:
,
если
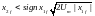 ;
;
,
если
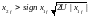 .
.
Рассмотрим для приведенного объекта синтез закона управления, который минимизирует интегральный квадратичный критерий
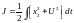
Введем переменную

и
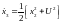 .
.
Функция Гамильтона для расширенной модели имеет вид
 .
.
Максимальное значение Н находим из условия
 .
.
Откуда находим оптимальный закон управления:
 .
.
Сопрягающая система имеет следующий вид:
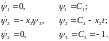
Перепишем уравнение для оптимального управления
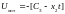 ;
;
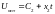 .
.
26.. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВААНИЕ. РЕКУРРЕНТНОЕ УРАВНЕНИЕ. УР-НИЕ ОПТИМ-СТИ. ПРОБЛЕМЫ ИССЛЕДОВАНИЯ.
Динамич-е програм-ние. В основу положен пр-п, получивший наимен-е пр-па оптимальности. Согласно этому пр-пу оптим-ное ур-ние опр-ся конечной целью управления и состоянием системы в рассматриваемый момент времени, независимо от того, каким образом система пришла в это состояние. Для любой оптимальной траектории каждый её участок, связывающий любую промежуточную точку этой траектории с конечной, также является оптимальной траекторией.
Пусть имеем дискретную модель объекта
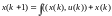 (6.45)
(6.45)
и
необх-о найти упр-щие возд-вия
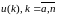 ,
которые обесп-т минимум кр-рия
,
которые обесп-т минимум кр-рия
 . (6.46)
. (6.46)
Следовательно, критерий оптимальности является функцией (n+1) переменных U(k), каждая из которых действует на своем временном интервале, что позволяет задачу расчленить на n-подзадач, связанных на соседних временных интервалах. В результате имеем последовательную цепочку простых задач, каждая из которых требует найти лишь одно управляющее воздействие для фиксированного интервала времени. При таком подходе, участки процесса рассматриваются в последовательности обратной их номеру от конца процесса к его началу.
Пусть структура процесса в виде отдельных участков имеет вид рис. 6.5.
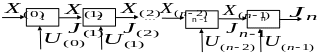
Рис. 6.5 Структура дискретного процесса управления
Для
последнего интервала времени, из
допустимого диапазона
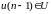 ,
при возможных значениях
,
при возможных значениях
 ,
можно выбрать такие
,
можно выбрать такие
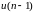 ,
которые минимизируют величину Jn.
,
которые минимизируют величину Jn.
Обозначим
минимальное значение Jn
через

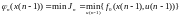 . (6.47)
. (6.47)
Затем переходим к предпоследнему интервалу времени n1. Значения входной координаты и управляющего воздействия здесь соответственно равны x(n2) и u(n2). Теперь минимизацию Jn-1 будем осуществлять с помощью управления u(n2), дополняя полученные решения результатами n для последнего участка. Вводя обозначения
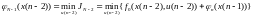
или с учетом модели движения объекта
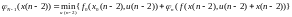 ,
,
расчеты, производимые аналогичным образом для произвольного интервала времени, можно записать в виде рекуррентной формулы
 (6.48)
(6.48)
Так продолжается расчет до тех пор, пока не приходим к первому интервалу с заданным значением х(0), что позволяет, используя модель динамики движения объекта для каждого такта, находить из ранее зафиксированных табличных значений оптимальные значения (Uопт(0), Uопт(1), Uопт(2), …).
Этот метод можно рассматривать как алгоритм для вычисления на ПЭВМ. Используем теперь идею динамического программирования для оптимизации управления в непрерывных процессах.
Пусть требуется выбрать x(t) таким образом, чтобы интеграл
 (6.49)
(6.49)
принял минимальное значение при движении из точки x(t0) в точку x(tf). Пусть (x, t) есть функция, соответствующая минимуму интеграла J с нижним пределом t:
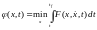 . (6.50)
. (6.50)
Минимизацию можно производить и по
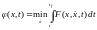 . (6.51)
. (6.51)
Для использования ранее рассмотренного принципа оптимальности разобьем траекторию движения системы на два интервала времени [t, t + ] и [t + , tf]. Первый интервал времени выбираем малым. Для этого интервала начальным условием является x(t), а для второго x(t+).
Перепишем функцию (x, t) к виду
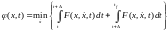 . (6.52)
. (6.52)
Воспользовавшись принципом оптимальности, можем считать, что для интервала [t + , tf] существует оптимальное решение. Это позволяет записать
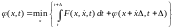 , (6.53)
, (6.53)
где
 .
.
Так как очень мало, то можно переписать
 .
.
Разложим в ряд Тейлора

и ограничимся линейными членами разложения. Тогда можно записать (x, t) следующим образом
 . (6.54)
. (6.54)
Выражение можно привести к виду:
 (6.55)
(6.55)
В пределе, когда стремится к нулю, запишем уравнение в виде
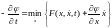 . (6.56)
. (6.56)
Если бы х был вектором, тогда уравнение записывается в виде
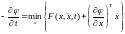 . (6.57)
. (6.57)
Назовем полученное уравнение уравнением Беллмана для непрерывных систем.
Рассмотрим пример управления объектом первого порядка
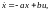
где
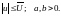
Пусть критерий качества системы имеет вид
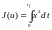 .
.
Введем функцию
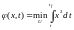 .
.
Используя уравнение Беллмана, запишем
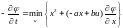 .
.
Функция в фигурных скобках достигает минимум при условии
 .
.
Оптимальное
управляющее воздействие принимает
значения +U
или U
в соответствии со знаком производной
 ,
удовлетворяющей дифференциальному
уравнению в частных производных
,
удовлетворяющей дифференциальному
уравнению в частных производных
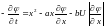 .
.
Аналитическое решение этой задачи трудно получить и поэтому часто используют численные методы. Как и в случае с принципом максимума, так и в случае использования динамического программирования, мы имеем проблему с нахождением функции (t).
