23. Синтез дискр-х компенс-х регулят-в из условия, обеспеч-х минимизацию дисперсии вых-го сигнала лин-й системы.

Регуляторами с минимальной дисперсией будем называть регуляторы, расчет которых основан на минимизации дисперсии регулируемой переменной у(t):

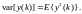
Ввиду того что в этот критерий не входит (со своим весом) управляемая переменная u(t), во многих случаях наблюдались весьма значительные изменения сигнала на входе регулятора. Поэтому и было предложено дополнить критерий взвешенным значением управляемой переменной и минимизировать величину

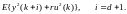
Шум n(k) обычно описывают как непараметрическими моделями (например, переходной характеристикой формирующего фильтра), так и параметрическими. Введение управляющего воздействия не позволяет получить минимум дисперсии регулируемой переменной; вместо нее минимизируется взвешенная сумма дисперсий регулируемой и управляемой переменных. Регуляторы, оптимизированные по такому критерию, будем именовать регуляторами с минимальной обобщенной дисперсией.

Ниже излагается методика расчета регуляторов с минимальной обобщенной дисперсией для объектов с запаздыванием и без него. Обычные рег-ры с мин-й дисперсией м.б. получены как частный случай при r=0. Для описания формирующих фильтров исп-ся параметрические модели, которые наиболее удобны при синтезе адаптивных алгоритмов управления, основанных на идентификации параметров.

Рег-ры с миним-й обобщенной дисперсией для объектов без запаздывания

Допустим, что объект управления имеет передаточную функцию

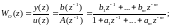(5.153)

формирующий фильтр шума –

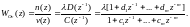(5.154)

Предполагается, что v(k) – это некоррелированный случайный сигнал, причем

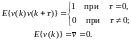(5.155)

Структурная схема рассматриваемой системы упр-я представлена на рис. 5.5.

Будем считать, что задающее воздействие w(k) = 0, при этом

e(k) = – y(k). Требуется построить регулятор, обеспечивающий минимум критерия

(5.156)

Этот регулятор должен вырабатывать такую последовательность входных воздействий u(k), которая минимизирует ошибку вида (5.156), вызванную случайным возмущением {v(k)}. Отметим, что

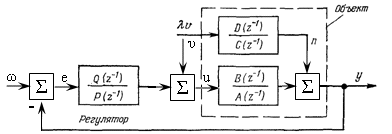
Рис. 5.5. Регулятор с минимальной обобщенной дисперсией в системе управления с объектом без запаздывания

в критерии качества I используют величину y(k + l), а не y(k), поскольку в исходной модели b₀ = 0 (т.е. прямая передача отсутствует), в силу чего управляющее воздействие u(k) не оказывает влияния на величину регулируемой переменной y(k). Ввиду этого необходимо выразить y(k + l) в функции ранее наблюдавшихся значений y(k), y(k – 1), …; u(k), u(k – 1), … . Согласно уравнениям (5.153) и (5.154), предсказанное значение y(k + l) можно получить из выражений:

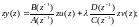(5.157)

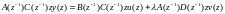. (5.158)

Последнее перепишем в развернутой форме:

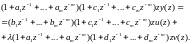(5.159)

Выполнив умножение и возвратившись во временную область, имеем

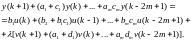(5.160)

Подставим полученное соотношение в критерий (5.156):

(5.161)

В м-нт времени k все в-ны, вх-щие в (5.161), известны, за искл-м u(k) и v(k + l). Поэтому, беря матем-е ожид-е последней, учтем, что она не зав-т от ост-х перем-х:

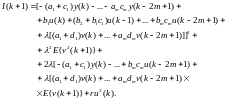(5.162)

Оптимальное значение управляющей переменной и(k) определим из условия

(5.163)

Преобр-ем множитель при b₁ в ур-нии (5.163), восп-вавшись соотн-м (5.160):

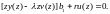(5.164)

Подставив выражение (5.157) в (5.164)

,

получим окончательный результат в виде передаточной функции регулятора с минимальной обобщенной дисперсией (далее он сокращенно именуется РМД1):

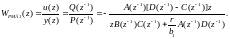(5.165)

Как следует из (5.165), в описание этого регулятора входят элементы модели объекта управления (полиномы A(z^–1) и В(z^–1)) и модели случайного возмущения (полиномы c(z^–1) и D(z^–1)). При r = 0 (5.165) дает упрощенный вариант регулятора с минимальной дисперсией (сокращенное обозначение – РМД2):

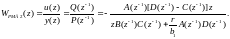(5.166)

В случае C(z^-1) = A(z^-1) передат-я ф-ция р-ра, обознач-го РМД3, приобр-т вид

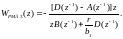(5.167)

При r = 0 (5.167) переходит в передаточную функцию регулятора РМД4:

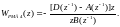(5.168)

Синтезир-е регуляторы существенно отличаются по своим характеристикам.

Рег-ры с мин-ной обобщенной дисперсией для объектов с запаздыванием

ОУ может опис-ся передат-й функцией, учитывающей наличие запаздывания:

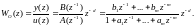(5.169)

С тр-ра системы упр-ния с объектом такого типа изображена на рис. 5.7. В систему вкл-н фильтр, форм-ющий

Рис. 5.7. Рег-р с мин-ой дисперсией в сист. упр-я с объектом, содерж-м запазд-е

в соотв-и с уравнением (5.154) случайное возмущение n(k) из белого шума v(k) с характеристиками (5.155). Поскольку управляющая переменная u(k), подаваемая на вход объекта с запаздыванием d, оказывает воздействие на значения регулируемой переменной, начиная лишь с y(k + d + l), используем в данном случае критерий

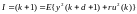. (5.170)

Согласно (5.157), предсказ-е знач-е y(k + d + l) можно опред-ть из соотношения

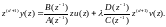(5.171)

В момент времени k, для которого рассчитывается управление u (k), значения случайного шума v(k + 1), …, v(k + d+ 1) еще неизвестны. Учитывая это, разделим выражение, описывающее формирующий фильтр в (5.171), на две части:

(5.172)

На рис. 5.7 формирующий фильтр также представлен в виде двух составляющих: F(z^-1), описывающей ту часть последовательности значений n(k), которые не могут быть подавлены за счет u(k), и

z^-(d+1)L(z^-1)/C(z^-1), соответствующей тем значениям n(k) в y(k), на которые u(k) воздействует. Введенные в (5.172) полиномы имеют вид

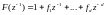, (5.173)

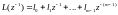. (5.174)

Их пар-ры можно опр-ть путем непоср-го сравн-я коэф-нтов при одинак-х степенях z в ур-нии. 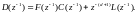(5.175)

Регуляторы с минимальной дисперсией без статического смещения

Для того чтобы постоянные внешние возмущения или ступенчатые изменения задающей переменной не приводили к появлению постоянных смещений регулируемой переменной, передаточная функция регулятора должна удовлетворять условию: 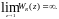(5.182)

Поскольку это усл-е не выполн-ся для синтезированных рег-ров с минимальной дисперсией, в их структуру должны быть внесены некоторые изменения.

а) Введение дополнительного интегрирующего члена

В простейшем случае для устранения статических смещений достаточно включить в передаточную функцию регулятора с минимальной дисперсией полюс в точке z = l. Более гибким методом является введение в регулятор

(5.183)

звена пропорционально-интегрирующего типа, описываемого перед-ной функцией

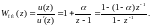(5.184)

Это равносильно добавлению разностного уравнения

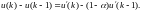(5.185)

Варьируя коэффициент , можно получать регуляторы с различными свойствами:

 = 0: u(k) = u'(k) – регулятор П–типа;

 = 1: u(k) – u(k – l) = u'(k)–рег-тор ПИ–типа с равными весами И– и П–звеньев.

Если   0, условие

выполняется для регуляторов РМД1 и РМД2 при D(1)  С(1), а для РМДЗ и РМД4 – при D(1)  A(1). В тех случаях, когда указанные соотношения между полиномами не соблюдаются, можно изменять их, вводя дополнительные полюса при z = l:

в РМД2 C'(z) = (z – l)C(z);

в РМДЗ и РМД4 A'(z) = (z – l)A(z).

Данный способ не дает желаемого эффекта лишь для регулятора РМД1.

Влючение в рег-р звеньев интегрирующего типа позволяет избавиться от статического смещения. В то же время это приводит к возрастанию дисперсии переменной y(k), особенно в случае высокочаст-ного возмущения v(k). Надлежащим выбором α можно добиться оптимального соотношения между этими явлениями.

Ранее синтез регуляторов с минимальной дисперсией проводился в предположении, что задающий сигнал отсутствует, т.е. w(k) = 0, ввиду чего y(k) = – e(k). Используя расширенный критерий качества

, (5.186)

можно минимизировать дисперсию регулируемой переменной в рабочей точке [w(k); u_w(k)], соответствующей ненулевому задающему сигналу. Здесь величина

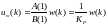(5.187)

равна такому значению u(k), при котором отсутствует статическое смещение, т.е. y(k) = w(k). Выполнив преобразования, получим уравнение модифицированного регулятора с минимальной дисперсией:

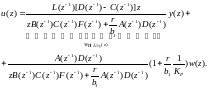(5.188)

Данный регулятор обеспечивает устранение смещений, возникающих в результате изменения задающей переменной w(k). Другой подход к построению регуляторов с аналогичными свойствами, основанный на оценивании параметров замкнутого контура управления.

б) Рег-торы с мин-й дисперсией для объектов типа чистого запаздывания

Полученные выше рег-торы с миним-й дисперсией обладают оптим-й стр-рой по отнош-ю к объектам вида (z~¹)z-d/A (z",¹) и формирующим фильтрам шума D(r^1)/С (z^1). При их выводе предполагалось, что объект описывается разностным ур-нием, в котором учтено наличие запазд-ия. В этом случае в системах с рег-рами РМД2-з и РМДЗ-з регулируемая переменная предст-ет собой процесс со скользящим средним порядка d, причем его дисперсия резко возрастает с ув-нием d.

Здесь мы рассмотрим регуляторы с минимальной дисперсией применительно к объектам, которые описываются моделями типа чистого запаздывания:

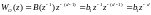. (5.189)

Воспользовавшись предыдущими рез-ами, получим след-е ур-ния регуляторов:

Для формирующего фильтра шума вида .

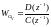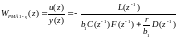, (5.190)

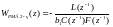, (5.191)

где, согласно (5.173)

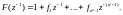(5.192)

В соответствии с (5.175) полиномы, входящие в формулы (5.190) и (5.191), связаны соотношением

. (5.193)

Следовательно, передаточные функции регуляторов отличаются от нуля только в тех случаях, когда полином С(z^1) имеет порядок m  l и/или D(z^1) – порядок m  d.

Для формирующего фильтра шума вида W_Ov(z^1) = D(z^1); C(z^1) = A(z^1) = l.

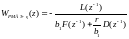; (5.194)

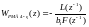. (5.195)

Согласно уравнению (5.175), в данном случае L(z^1) = 0 (т.е. регулятор нереализуем), если у полинома D(z^1) порядок m < d – 1. Это еще раз подтверждает принцип, лежащий в основе синтеза регуляторов с минимальной дисперсией. Он состоит в получении оценки регулируемой переменной y(k – f – d + 1) по известным значениям u(k – 1), u(k – 2), ... и v(k – 1), v(k – 2), .... Предсказанная оценка используется далее для вычисления управляющего сигнала u(k). В соответствии с уравнением (5.172) значения регулируемой переменной и элементов последовательности случайного шума связаны соотношением

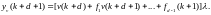(5.196)

Очевидно, данная величина при m  d – 1 не поддается оценке, ввиду чего регулирование невозможно. Если m = d – 1, то

. (5.197)

В этом случае D(z^1) = F(z^1), т.е. возмущающий сигнал содержит только те составляющие, на которые не воздействует управление u(k). Следовательно, регулятор с минимальной дисперсией при m = d – 1 не оказывает никакого влияния на функционирование замкнутого контура управления. Только при m  d регулятор этого типа позволяет уменьшить дисперсию y(k) по сравнению с той, которая наблюдается на выходе разомкнутого контура.

Т.о., если модель ОУ п/с чистое запазд-е, рег-ры с миним-й дисперсией способны повысить кач-во упр-ния лишь в том случае, когда возмущение n(k), действующее на y(k), является авторегрес-ным процессом со скользящим средним (окрашенным шумом) или процессом со скользящим средним порядка m  d.