21.. Синтез дискретных компенсационных регуляторов из условия обеспечения желаемого времени регулирования.

Обычный апериодический регулятор Предп-ся, что ступенч-е измен-е задающей переменной происходит в момент времени k = 0, т. е.

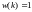для (5.37)

Если время запаздывания d = 0, то требования для минимального конечного времени установления переходного процесса записываются следующим образом:

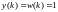для ,

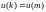для . (5.38)

Для случая b₀ = 0 z-преобр-я зад-щей, регулир-й и упр-щей перем-х им-т сл-й вид:

(5.39)

, (5.40)

. (5.41)

Разделив уравнения (5.40) и (5.41) на (5.39), получим

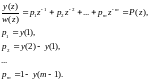(5.42)

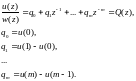(5.43)

Следует учесть, что

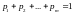, (5.44)

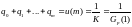. (5.45)

Передаточная функция замкнутой системы будет равна

. (5.46)

Следовательно, передаточная функция компенсационного регулятора имеет вид

. (5.47)

Сравнивая уравнения (5.42) и (5.46), получим

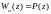. (5.48)

Более того, из уравнений (5.42) и (5.43) следует, что

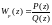, (5.49)

и с учетом (5.47) передаточная функция регулятора принимает вид

. (5.50)

Параметры этого регулятора можно получить, используя уравнения (5.49), (5.44) и (5.45):

,

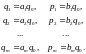(5.51)

Таким образом, параметры регулятора могут быть вычислены очень просто. Начальное значение управляющей переменной u(0) зависит только от значения суммы коэффициентов b₁ объекта. Поскольку значение этой суммы убывает с уменьшением такта квантования, начальное значение управляющей переменной u(0) будет тем больше, чем меньше такт квантования.

Такой апериодический регулятор можно считать компенсационным регулятором (см. 5.47), однако передаточную функцию замкнутой системы (5.44) и (5.42) в данном случае определяют в процессе проектирования, а не задают заранее. Результирующая передаточная функция замкнутой системы с учетом уравнений (5.48) и (5.42) принимает вид

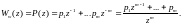
Ее характеристическое уравнение равно

(5.52)

Таким образом, контур управления с апериодическим регулятором имеет m полюсов в начале координат плоскости z.

Если d  0, необходимо использовать следующую модель объекта:

(5.53)

Коэффициенты этой модели удовлетворяют соотношениям

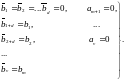(5.54)

На процесс управления наложены теперь следующие ограничения:

(5.55)

Далее можно применить уравнения (5.39)  (5.51), учитывая (5.53). Из уравнений (5.53) и (5.49) следует, что

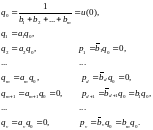(5.56)

Следовательно, передаточная функция регулятора имеет вид

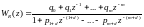. (5.57)

Из уравнений (5.56) и (5.57) получим передаточную функцию апериодического регулятора АР(v):

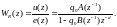(5.58)

Отсюда следует, что передаточная функция по задающему сигналу при использовании точной модели объекта будет равна

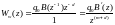, (5.59)

а ее характеристическое уравнение есть

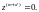(5.60)

Следует иметь в виду, что прим-ие апер-го рег-ра приводит к сокр-ю полюсов ОУ-.

Апериодический регулятор повышенного порядка

Если ув-ть конечное время устан-я на 1 такт с m до m + 1, то можно заранее опр-ть нач-е знач-е управляющей переменной u(0). Поскольку этот сигнал обычно имеет максим-ю в-ну, его можно огран-ть, задав допустимое знач-е u(0) при синтезе р-ра.

Добавим еще 1 член в ур-ния (5.40) и (5.41), тогда ур-ния (5.42) и (5.43) примут вид

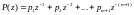, (5.61)

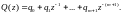(5.62)

Приравнивая коэф-нты этих полиномов коэф-нтам из уравнения (5.49), получим

(5.63)

Это рав-во справедливо только в том случае, когда его правая часть содержит общий корень в числителе и знаменателе. Таким образом,

. (5.64)

После деления на q'₀, пол-м связь м/д коэф-ми ур-ия (5.64) и коэф-ми ур-ния (5.63):

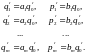(5.65)

Теперь выпишем пар-тры полных полиномов числ-ля и знаменателя ур-ния (5.64) и, прир-ая коэф-нты в правых частях ур-ний (5.63) и (5.64), запишем след-е соотн-я:

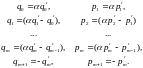(5.66)

Из уравнения (5.43) имеем

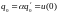, (5.67)

а из уравнений (5.61) или (5.42) получим

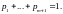
Наконец, из уравнений (5.66) и (5.65) следует, что

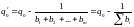. (5.68)

Теперь на основании уравнений (5.67) и (5.68) можно записать соотношения для определения параметров регулятора:

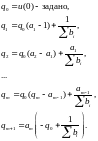(5.69)

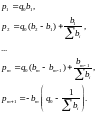(5.70)

По аналогии с уравнением (5.50) запишем передаточную функцию регулятора

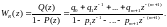(5.71)

однако в отличие от регулятора, описываемого выражением (5.50), в данном случае начальное значение управляющей переменной u(0) задано. Второе значение управляющей переменной в соответствии с уравнениями (5.43) и (5.69) будет равно

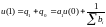. (5.72)

Значение u(0) не следует задавать слишком малым, так как при этом u(1) будет больше u(0), что в большинстве случаев нежелательно.

Для выполнения условия u(l)  u(0) необходимо, чтобы удовлетворялось соотношение

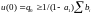. (5.73)

Выполнение условия u(l)  u(0) вовсе не гарантирует, что |u(k)| < |u(0)| для k  2. Поскольку расчет параметров регулятора достаточно прост, значение u(0) обычно изменяют до тех пор, пока не будет получена желаемая последовательность управляющих сигналов. Часто условие u(l) = u(0) приводит к хорошим результатам.

Для объектов с запаздыванием (d > 0) расчет регулятора выполняют с использованием уравнений (5.535.57). В этом случае передаточная функция апериодического регулятора AP(v + l), определяемая уравнением (5.71) и соотношениями (5.69) и (5.70), принимает вид

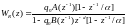, (5.74)

где

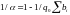. (5.75)

Характеристическое уравнение регулятора записывается следующим образом:

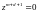. (5.76)