18)Синтез многосвязных линейных систем с исп-ем модального управления и компенсаторов

Задача: при известных дин-х хар-х объекта управления, заданных соответ-ми передаточными матрицами, опред-ть стр-ру и эл-ты матрицы регулятора т.о., ч/бы при устан-х воздей-х хар-р перехода сис-мы в новое установ-ся состояние минимально отличался от заданного.

Пусть S(p)-n-мерная вектор-фун-я заданных вых-х хар-к сис-мы при станд-х вых-х сиг-х. в кач-ве вх-х сиг-в примем единичный скачок. В кач-ве обобщ-х динам-х хар-к м. исп-ть изображения переходных хар-к:

S1(p)= k_i(a_ip+d_i) / p(b_ip²+c_ip+l_i)(γ_ip+1) (1)

C учетом передаточной матрицы объекта и вых-х хар-к (1) м. найти вектор операторов на входе в объект или вых-в рег-ра:

U(p)=[Wоб(p)]^-1S(p)

Пусть сис-ма им-т стр-ю сх. изображ-ю на рис-ке:

Если при синтезе сис-мы исп-ть скачкообразные вх-е сигналы, то получаем:

ε(p)=(1/p)[I-S(p)]

Зная u(p) и ε(p) м. найти передаточную матрицу регулятора:

Wp(p)=[(1/p)I-S(p)]^-1[Wоб(p)]^-1

19)Методы фазовой траектории при исследовании нелинейных систем

Пусть им-ся с-ма, опис-ся 2-мя нелин-ми ур-ми:

→

→

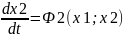М. построить «семейство» фазовых траекторий для разных н.у. и м. обнаружить общие признаки для этих траекторий.

[ x1^*; x2^*]

Точки, кот. дают такой результат, наз-т особыми.

Построим фазовые траектории для лин-х сис-м II порядка:

Перейдем к модели в переменных состояния y=x1

;

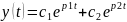
Если корни ХАУ вещественны и «+»ны, то сис-ма неустойчива. Если линии входят в начало коор-т, то сис-ма устойчива и наоборот:

→

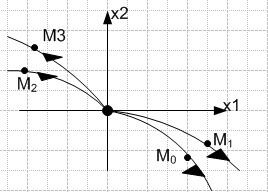
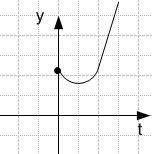
Портрет типа «седло» - вещественные корни равны p1=1; p2=-2

↓

П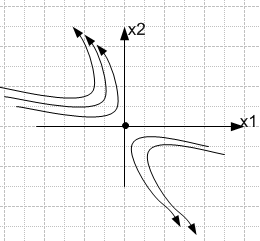 ортрет типа «фокус»

Возьмем комплексные корни: p1=-1+j2; p2=-1-j2

→

p1=1+j2; p2=1-j2

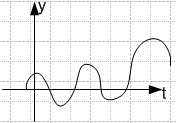
Е сли корни чисто мнимые: p1=j2; p2=-j2 портрет типа «центр»

→

20)Метод гармонической линеаризации и его исп-е при анализе и синтезе сис-м управления

М-д гармонич. линеаризации-осн-н на том, что в силу фильтрующих или резонансных св-в сис-мы, дв-е в кот-ой близко к синусоидальному, при исследовании периодического режима м. принимать во внимание только основную гармонику. Пусть замкнутая с-мв состоит из нелин-го безынерционного эл-та с хар-ой: ξ=φ(σ) (1) и инерц-ой линейной части, описываемой комплексной ПФ Wл(jω). Если на вход нелин-го звена дей-т гармонический сигнал: σ=asinωt (2), то первая гармоника на выходе нелин-го эл-та: ξ=B1sinωt+A1cosωt (3), где B1, A1 опред-ся как коэф-ты ряда Фурье:

Обозначив B1/a=q(a) и A1/a=q’(a), перепишем (3) в виде ξ=q(a)asinωt+q’(a)acosωt (6). Учитывая, что asinωt=σ; acosωt=ρ/ω*σ, получим:

ξ =φ(σ)=[q(a)+q’(a) ρ/ω]σ (7)- гармоническая линеаризация, коэф-ты q(a); q’(a)-коэф-ты гарм-ой линеаризации. На основании (7) нах-м ПФ линеариз-го нелин-го эл-та:

Wн(a,p)=q(a)+q’(a) ρ/ω (8) и АФХ Wн(a)=q(a)+jq’(a) (9)

Используя подстановку ψ=ωt и формулы для выч-я B1 и A1:

(10)

На основании (10) рассчит-т коэф-ты нелинейностей. Если нечетно-симметричная нелинейность однозначна, то:

q’=0, а φ(σ)=q(a)σ (11)

С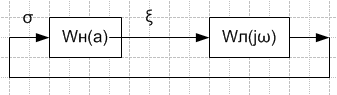 труктурная сх. линеаризованной сис-мы:

По Найквисту: Wл(j𝛚)=-1/Wн(a)