14) Синтез системы регулирования методом расчета параметров рег-ра на желаемый показатель колебательности

Задаемся W_РЕГ. =arcSin(1/M_ЖЕЛ). Имеем систему вида:

Передаточная ПИ-регулятора имеет вид: .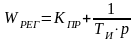

Строим АФЧХ, при К_ПР=1 для построения интегральной составляющей:

, где окружность строится:

Где L=1/K_{ПР.РАСЧ.}. Зададимся численными значениями Т_И=1;5;10;100;…

Строим один график для К_ПР=1, Т_И=5 и т.д.получим семейство кривых, причем 1/ Т_Иjw= -j(1/ Т_Иw). Знак минус означает поворот по часовой стрелке(*). Задаемся частотами w [w₁, w₂, …w_n], находим 1/ Т_Иw_i. Получим новую кривую, проводим окружностьполучаем L K_{ПР.РАСЧ}=1/ L.

Kпр д.б. таким ч/бы умножив его на плечо L, мы получили 1.

Составляем таблицу:

ТИ	1	5	10	100
KПР.РАСЧ

Строим график

Точка А является лучшим вариантом.

15)Синтез системы управления с использованием упредителей Смита

Пусть объект содержит большое запаздывание. На систему действует возмущающее воздействие F. Передаточная объекта:

Сложность – в запаздывании, решение этой задачи предложил Смит:

Упредитель Смита – пунктиром.

Имея эту структурную схему, можем попробовать записать связь выхода системы с задающим воздействием и возмущающим.

,

F=0, , ,

16)Синтез инвариантных систем управления

Задачи инвариантности-обеспечение независимости каких-то координат от возмущающих воздействий.

Пусть сис-ма опис-ся сис-ой ур-й:

a11x1+a12x2+a13x3=ν(t);

a21x1+a22x2+a23x3=0;

a32x2+a33x3=0. На основании ур-й м. составить стр-ю сх-му, позвол-ю нах-ть переменные x:

И з сх. видно, что возмущение ν(t) напрямую влияет на корд-ту x1. При такой стр-ре сис-мы почти невозможно обеспечить инвар-ть координаты x1. Изменим порядок ур-й:

a21x1+a22x2+a23x3=0;

a32x2+a33x3=0

a11x1+a12x2+a13x3=ν(t);

Сост-м новую стр-ю схему:

Вторая стр-я сх. им-т два

Канала для направления

возд-й от возмущения ν к переменной х1. Наличие 2

каналов позволяет

организ-ть прох-е возмущ-я

т.о., ч/бы суммарный эф-т

от возмущ-я сводился к нулю(пр-п двухканальности).

Возьмем одноконтурную систему:

В данной сис-ме возмущение доступно измерению, что позвол-т ис-но создать 2 канал для прох-я возмущения на выход сис-мы:

У словие компенсации на основании стр-ой схемы:

νWкомп(p)Wр(p)=νWν(p);

Wкомпен-ра(p)= Wν(p)/ Wр(p);

17)Многосвязные линейные сис-мы и их анализ

Многосвязный объект управ-я сод-т m управ-х каналов и n выходов.

В этих сис-х присутствует взаимосвязь каналов. Учет взаимосвязи каналов яв. одним из важнейших требований при синтезе систем управления такими объектами. Для этого восп-ся м-дом Бристоля, кот. заключается в построении спец-ой матрицы:

элементы кот-ой в статике соот-т соотношению λ_1j=(dy_i/du_j)/(dy_i/du_j)_c (все контуры разомкнуты/все контуры, кроме u_c, замкнуты), где yi-установившееся значение i-го выхода, uj-управление. Необходимо опред-ть коэф-ты передаточной матрицы:

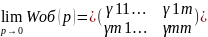
Затем надо найти элементы матрицы: [ ]^-1

Элементы матрицы Λ нах-ся из выражения: ^-1ij путем перемножения элементов с одинаковыми индексами. Анализ матрицы Λ показывает, что сис-ма имеет слабую связанность, если диагональные элементы близки к единице, а недиагональные сущ-но меньше (близки к нулю). Один из первых методов синтеза систем был основан на компенсации или развязывании перектестных связей объекта и получил название автономного регулиолвания. Авт-е рег-е обеспечивает раздельное управление выходами объкта за счет вкл-я в состав системы компенсатора, напр., м/ду рег-ром и объектом. Передаточная матрица расширенного объекта равна: Wоб(p)Wк(p)=Wр.об.(p). В кач-ве эл-тов передаточной матрицы расшир-го объекта принимаются диагональные элементы передаточной матрицы исх. объекта:

Wр.об.=W011(p) 0 0 … 0

0 W022(p) 0 … 0

. . . . .

. . . . .

0 0 0 … W0nn(p)

Или

Wр.об.(p)=diagWоб(p)

Тогда м. найти передаточную матрицу компенсатора:

Wk(p)=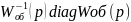

Полученные матем-м путем результаты требуют оценки из усл-й их физ-ой реализуемости.