
- •2.Глав. Вектор и глав. Момент сил.
- •3.Мом. Силы относ. Точки.Т Вариньона
- •4.Теоремы о парах сил.
- •5.Теорема о переносе сил в произвольную точку.
- •7.Расчёт ферм.
- •11.Вращательное движение вокруг неподвижной точки.Теорема Эйлера.
- •17.Силы постоян., перемен., зависящие от расстояния,зависящие от скорости,зависящие от времени.
- •19.Прицип относительности классической механики.
- •20. Теор. О движ. Ц.М. Сист.
- •22.Теор об изменении количества движения механич сист.
- •24.Теорема об изменении момента количества движения механической системы. Следствие.
- •26. Прецессия гироскопа
- •27.Теорема о движении центра масс системы. Следствие.
- •28. Теория удара. Удар тела о неподвижную преграду. Коэффициент восстановления при ударе.
26. Прецессия гироскопа
Наблюдать прецессию достаточно просто. Нужно запустить волчок и подождать, пока он начнёт замедляться. Первоначально ось вращения волчка вертикальна. Затем его верхняя точка постепенно опускается и движется по расходящейся спирали. Это и есть прецессия оси волчка.
Главное свойство прецессии — безынерционность: как только сила, вызывающая прецессию волчка, пропадёт, прецессия прекратится, а волчок займёт неподвижное положение в пространстве. В примере с волчком этого не произойдет, поскольку в нём вызывающая прецессию сила — гравитация Земли — действует постоянно.
Можно получить эффект прецессии, не дожидаясь замедления вращения волчка: толкните его ось (приложите силу) — начнётся прецессия. С прецессией напрямую связан другой эффект, показанный на иллюстрации ниже — этонутация — колебательные движения оси прецессирующего тела. Скорость прецессии и амплитуда нутации связаны со скоростью вращения тела (изменяя параметры прецессии и нутации в случае, если есть возможность приложить силу к оси вращающегося тела, можно изменить скорость его вращения).
27.Теорема о движении центра масс системы. Следствие.
Теорема о движении центра масс системы.
Произведение
массы системы на ускорение ее центра
масс равно геометрической сумме всех
действующих на систему внешних сил
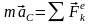 – дифференциальное уравнение движения
центра масс. В проекциях на оси координат:
– дифференциальное уравнение движения
центра масс. В проекциях на оси координат:
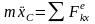 .
.
Закон
сохранения движения центра масс.
Если главный вектор (векторная сумма)
внешних сил остается все время равным
нулю, то центр масс механической системы
находится в покое или движется прямолинейно
и равномерно. Аналогично в проекциях
на оси, если
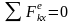
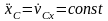 ,
если при этом в начальный момент vCx0=
0, то
,
если при этом в начальный момент vCx0=
0, то
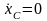
xC=
const.
xC=
const.
28. Теория удара. Удар тела о неподвижную преграду. Коэффициент восстановления при ударе.
Удар твёрдых тел, совокупность явлений, возникающих при столкновении движущихся твёрдых тел, а также при некоторых видах взаимодействия твёрдого тела с жидкостью или газом.
Восстановления коэффициент в теории удара, величина, зависящая от упругих свойств соударяющихся тел и определяющая, какая доля начальной относительной скорости этих тел восстанавливается к концу удара. В. к. характеризует потери механической энергии соударяющихся тел вследствие появления в них остаточных деформаций и их нагревания. При прямом ударе тела о неподвижную преграду (плиту) В. к. k = u/v, где v и u — скорости тела в начале и в конце удара по отношению к плите. Для тел из дерева k = 1/2, из стали ~ 5/9, из слоновой кости ~ 8/9, из стекла ~ 15/16.
29. Центр. удар 2 тел.Обмен скорост.
Центральный удар двух тел.Закон сохранения импульса: полный импульс замкнутой системы остается постоянным.
Для замкнутой системы будут сохраняться и проекции импульса на координатные оси:
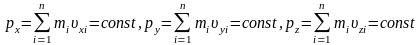 .
.
Рассмотрим центральный удар двух тел. Центральным называется удар, при котором тела движутся вдоль прямой, соединяющей их центры масс. Выделяют два предельных вида такого удара: абсолютно упругий и абсолютно неупругий.
Для
двух тел массами m1
и
m2
,
движущихся со скоростями
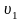 и
и
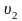 вдоль оси х, проекции их скоростей на
ось х после абсолютно упругого центрального
удара можно найти по формулам:
вдоль оси х, проекции их скоростей на
ось х после абсолютно упругого центрального
удара можно найти по формулам:
 ;
;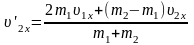 .
.
При этом сохраняются импульс и механическая энергия системы тел.
Если
удар абсолютно неупругий, то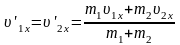 .
.
Тела после такого удара движутся вместе. Импульс системы тел сохраняется, а полная механическая энергия не сохраняется. Часть механической энергии переходит в энергию неупругой деформации и во внутреннюю энергию тел.
30.. Прям. центр. удар 2 тел.Т.Карно.
Карно теорема, 1) теорема о коэффициенте полезного действия тепловых двигателей. Согласно К. т., кпд Карно цикла не зависит от природы рабочего вещества и конструкции теплового двигателя и определяется только температурами нагревателя и холодильника. 2) В теории удара — теорема о потере кинетической энергии при абсолютном неупругом ударе: Кинетическая энергия, потерянная системой при ударе, равна той кинетической энергии, которую имела бы система, если бы её точки двигались с потерянными скоростями, т. е.
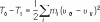 ,
где
,
где
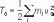 и
и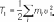 — кинетическая энергия системы
соответственно до и после удара, mi —
масса i-й точки системы, u0i и u1i — скорости
i-й точки до и после удара, (u0I — u1i) — т.
н. потерянная скорость точки.
— кинетическая энергия системы
соответственно до и после удара, mi —
масса i-й точки системы, u0i и u1i — скорости
i-й точки до и после удара, (u0I — u1i) — т.
н. потерянная скорость точки.
31. КПД кузнечного молота, КПД копра.
32.Удар по вращаемуся телу. Центр удара.
При
исследовании удара по вращающемуся
телу кроме теоремы об изменении количества
движения приходится использовать и
закон моментов. Относительно оси вращения
его запишем так 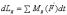 и,
после интегрирования за время
удара
и,
после интегрирования за время
удара  ,
, 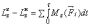 или
или 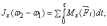 где
где 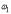 и
и 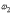 -
угловые скорости тела в начале и в конце
удара,
-
угловые скорости тела в начале и в конце
удара, 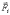 -
ударные силы.
-
ударные силы.
Правую часть надо немного преобразовать. Найдем, сначала, интеграл момента ударной силы относительно неподвижной точки О:
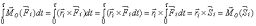 .
.
При
этом предполагалось, что за малое время
удара τ радиус-вектор 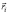 считался
неизменным, постоянным.
считался
неизменным, постоянным.
Проектируя
результат этого векторного равенства
на ось вращения z,
проходящую через точку О,
получим 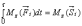 ,
т.е. интеграл равен моменту вектора
импульса ударной силы относительно оси
вращения. Закон моментов в преобразованном
виде запишется, теперь, так:
,
т.е. интеграл равен моменту вектора
импульса ударной силы относительно оси
вращения. Закон моментов в преобразованном
виде запишется, теперь, так:
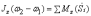 . (10)
. (10)
В качестве примера рассмотрим удар вращающегося тела о неподвижную преграду.
Тело,
вращаясь вокруг горизонтальной оси О,
ударяется о преграду А (рис.114).
Определим ударные импульсы сил,
возникающих в подшипниках на оси, 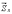 и
и 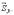
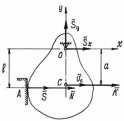
Рис.114
По
теореме об изменении количества
движения 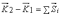 в
проекциях на оси х и у получим
два уравнения:
в
проекциях на оси х и у получим
два уравнения:
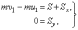
где
скорости центра масс С в
начале и конце удара 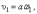
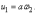 Поэтому
первое уравнение станет таким
Поэтому
первое уравнение станет таким 
Третье
уравнение, по (10), получится в виде 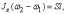 из
которого находим
из
которого находим 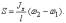
И, так как коэффициент восстановления
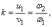
то 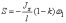 (в
нашем примере
(в
нашем примере 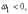 поэтому
ударный импульс S >
0, то есть направлен так, как показано
на рисунке).
поэтому
ударный импульс S >
0, то есть направлен так, как показано
на рисунке).
Находим
импульсы реакции оси: 
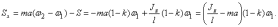
Обязательно
надо обратить внимание на то, что
при 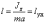 ударные
импульсы в подшипниках оси будут равны
нулю.
ударные
импульсы в подшипниках оси будут равны
нулю.
Место,
точка удара, расположенная на этом
расстоянии 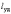 от
оси вращения, называется центром
удара.
При ударе по телу в этом месте ударные
силы в подшипниках не возникают.
от
оси вращения, называется центром
удара.
При ударе по телу в этом месте ударные
силы в подшипниках не возникают.
Кстати, заметим, что центр удара совпадает с точкой где приложены равнодействующая сил инерции и вектор количества движения.
Вспомним, что при ударе длинной палкой по неподвижному предмету, мы нередко испытывали рукой неприятный ударный импульс, как говорят – «отбивали руку».
Нетрудно найти в этом случае центр удара – место, которым следует ударить, чтобы не почувствовать это неприятное ощущение (рис.115).
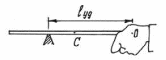
Рис.115
Так
как 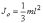 (l –
длина палки) и
(l –
длина палки) и 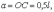 то
то
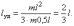
Следовательно, центр удара находится на расстоянии трети длины от конца палки.
Понятие центра удара учитывают при создании различных ударных механизмов и других конструкций, где встречаются ударные процессы.
[Введите текст]
