22.Теор об изменении количества движения механич сист.

Изменение количества движения мех. сис. за некотрый промежуток времени равно геометрической сумме импульсов внешних сил приложенных к системе за тотже промежуток времени.

K = ∑ m_кυ_к; K = ∑ m_кdr_к/dt = d/dt * ∑m_кr_к = d/dt * mr_c = mdr_c/dt = mυ_c => K = mυ_c. Найдём призводную: dK/dt = d(mυ_c)/dt = mdυ_c/dt = ma_c

Но из теоремы о движении ценра масс мех. сис. ma_c = R^E = ∑ P_к^E; dK/dt = ∑ P_к^E. Проинтегрируем это выражение: ∫_к1^к2 dK = ∫_t1^t2∑P_к^Edt;

k₂-k₁=∑S_к^E – ч.т.д.

Из теоремы об изменении количества движения системы можно получить следую­щие важные следствия:

1) Пусть сумма всех внешних сил, действующих на систему, равна нулю:

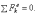
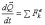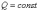Тогда из уравнения   следует, что при этом  . Таким образом, если сумма всех внешних сил, действующих на систему, равна нулю, то вектор количества движения системы будет постоянен по модулю и направлению.

2) Пусть внешние силы, действующие на систему, таковы, что сумма их проекций на какую-нибудь ось (например Оx) равна нулю:

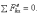
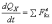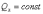Тогда из уравнения   следует, что при этом  . Таким образом, если сумма проекций всех действующих внешних сил на какую-нибудь ось равна нулю, то проекция количества движения системы на эту ось есть величина постоянная.

Эти результаты и выражают закон сохранения количества движения системы.

23.

Тело переменной массы , масса которого непрерывно изменяется с течением времени m= f(t) (пр.: ракета, топливо которой убывает). Дифф-ное уравнение движения точки переменной массы:

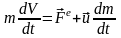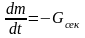– уравнение Мещерского, u – относительная скорость отделяющихся частиц. – реактивная сила, — секундный расход топлива, 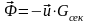. Реактивная сила направлена в противоположную сторону относительной скорости истечения топлива.

Формула Циолковского: 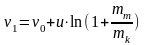— определяет скорость ракеты, когда все топливо будет израсходовано – скорость в конце активного участка, m_т– масса топлива, m_k– масса корпуса ракеты, v₀ – начальная скорость. 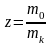– число Циолковского, m₀ – стартовая масса ракеты. От режима работы ракетного двигателя, т.е. от того насколько быстро сжигается топливо, скорость ракеты в конце периода горения не зависит. Для достижения 1-ой космической скорости 7,9 км/с, при m₀/m_k= 4, скорость отброса должна быть 6 км/с, что трудно осуществить, поэтому применяются составные (многоступенчатые) ракеты.

24.Теорема об изменении момента количества движения механической системы. Следствие.

 кинетический момент, одна из мер механического движения материальной точки или системы. Особенно важную роль М. к. д. играет при изучении вращательного движения. Как и для момента силы, различают М. к. д. относительно центра (точки) и относительно оси.

Для вычисления М. к. д. k материальной точки относительно центра О или оси z справедливы все формулы, приведённые для вычисления момента силы, если в них заменить вектор F вектором количества движения mv. Т. о., ko = [r · mu], где r — радиус-вектор движущейся точки, проведённый из центра О, a kz равняется проекции вектора ko на ось z, проходящую через точку О. Изменение М. к. д. точки происходит под действием момента mo(F) приложенной силы и определяется теоремой об изменении М. к. д., выражаемой уравнением dko/dt = mo(F). Когда mо(F) = 0, что, например, имеет место для центральных сил, движение точки подчиняется площадей закону.

25.свободный гироскоп. Теорема Резаля. Устойчивость гироскопа.

Свободным называется гироскоп, имеющий три степени свободы (по осям х, у и z) при отсутствии трения в осях. При этом неподвижная точка совпадает с точкой пересечения осей подвеса ротора и совмещена с центром тяжести гироскопа.

,

(5.11)

где 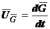  - скорость конца вектора кинетического момента  .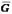

Выражение (5.11) представляет собой математическую запись в векторной форме теоремы Резаля, согласно которой: «Скорость конца вектора кинетического момента 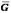  по величине и направлению равна моменту внешних сил».

Свободный гироскоп, раскрученный вокруг оси симметрии, обладает весьма значительной устойчивостью. Из основного уравнения моментов следует, что изменение момента импульса

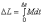                          (4)

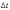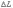Если интервал времени  мал, то и  мало, то есть при кратковременных воздействиях даже очень больших сил движение гироскопа изменяется незначительно. Гироскоп как бы сопротивляется попыткам изменить его момент импульса и кажется "затвердевшим".

Возьмем гироскоп конусообразной формы, опирающийся на стержень подставки в своем центре масс О (рис. 91). Если тело гироскопа не вращается, то оно находится в состоянии безразличного равновесия, и малейший толчок сдвигает его с места. Если же это тело привести в быстрое вращение вокруг своей оси, то даже сильные удары деревянным молотком не смогут сколько-нибудь значительно изменить направление оси гироскопа в пространстве. Устойчивость свободного гироскопа используется в различных технических устройствах, например, в автопилоте.
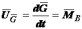