
- •2.Глав. Вектор и глав. Момент сил.
- •3.Мом. Силы относ. Точки.Т Вариньона
- •4.Теоремы о парах сил.
- •5.Теорема о переносе сил в произвольную точку.
- •7.Расчёт ферм.
- •11.Вращательное движение вокруг неподвижной точки.Теорема Эйлера.
- •17.Силы постоян., перемен., зависящие от расстояния,зависящие от скорости,зависящие от времени.
- •19.Прицип относительности классической механики.
- •20. Теор. О движ. Ц.М. Сист.
- •22.Теор об изменении количества движения механич сист.
- •24.Теорема об изменении момента количества движения механической системы. Следствие.
- •26. Прецессия гироскопа
- •27.Теорема о движении центра масс системы. Следствие.
- •28. Теория удара. Удар тела о неподвижную преграду. Коэффициент восстановления при ударе.
7.Расчёт ферм.
Фермой называется жесткая конструкция из прямолинейных стержней, соединенных на концах шарнирами. Если все стержни фермы лежат в одной плоскости, ферма называется плоской. Места соединения стержней фермы называют узлами. Все внешние нагрузки к ферме прикладываются только в узлах. Расчет фермы сводится к определению опорных реакций и усилий в ее стержнях.
Опорные реакции можно найти обычными методами статики, рассматривая ферму в целом как твердое тело.
Метод вырезания узлов. Этим методом удобно пользоваться, когда надо найти усилия во всех стержнях фермы. Он сводится к последовательному рассмотрению условий равновесия сил, сходящихся в каждом из узлов фермы.
Метод сечений (метод Риттера). Этим методом удобно пользоваться для определения усилий в отдельных стержнях фермы, в частности, для проверочных расчетов. Идея метода состоит в том, что ферму разделяют на две части сечением, проходящим через три стержня, в которых (или в одном из которых) требуется определить усилие, и рассматривают равновесие одной из этих частей. Действие отброшенной части заменяют соответствующими силами, направляя их вдоль разрезанных стержней от узлов, т. е. считая стержни растянутыми (как и в методе вырезания узлов). Затем составляют уравнения равновесия, беря центры моментов (или ось проекций) так, чтобы в каждое уравнение вошло только одно неизвестное усилие.
8.Способы задания движ. в кинемат.
Движение точки может быть задано тремя способами: естественным, векторным и координатным.
При
естественном способе задания движения
дается траектория, т. е. линия, по которой
движется точка
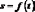
При
векторном способе задания движения
точки положение точки определяется
величиной и направлением радиуса-вектора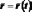
При
координатном способе задания движения
положение точки по отношению к выбранной
системе отсчета определяется при помощи
прямоугольной системы декартовых
координат
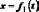
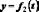
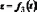
9. .Кинематич. анализ кривол. движ. в ест. сист. корд.
Кинемат
анализ крив:
естеств.
сист. отсч.:1)нуль отсч-в точке,2)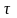 -касат, напр в стор движения,3)n-нормаль
к центру,4)в-бинормаль.(*1)
-касат, напр в стор движения,3)n-нормаль
к центру,4)в-бинормаль.(*1)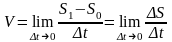
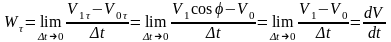
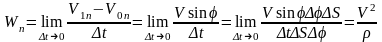 .
.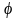 -угол
поворота,
-угол
поворота,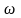 -угл
скорость
-угл
скорость
Если
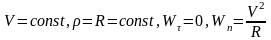 (*2)
(*2)
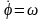 -угл
скор
-угл
скор
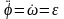 -угл
ускор,
-угл
ускор,
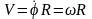 ,
,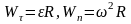 ,
,

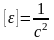 ;
;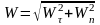
10. Поступательное и вращательное движение твердого тела
1. Поступательным называется такое движение абсолютно твердого тела, при котором любая прямая, жестко связанная с телом, перемещается параллельно самой себе. Все точки тела, движущегося поступательно, в каждый момент времени имеют одинаковые скорости и ускорения, а их траектории полностью совмещаются при параллельном переносе. Поэтому кинематическое рассмотрение поступательного движения абсолютно твердого тела сводится к изучению движения любой его точки. В самом общем случае поступательно движущееся твердое тело обладает тремя степенями свободы.
2. Движение абсолютно твердого тела, при котором две его точки А и B остаются неподвижными, называется вращением (вращательным движением) вокруг неподвижной прямой АВ, называемой осью вращения. При вращении твердого тела вокруг неподвижной оси все его точки описывают окружности, центры которых лежат на оси вращения, а плоскости - перпендикулярны к ней. Тело, вращающееся вокруг неподвижной оси, обладает одной степенью свободы: его положение полностью определяется заданием угла f поворота из некоторого начального положения.
3. Угловой скоростью вращения твердого тела называется вектор w, численно равный первой производной от угла поворота по времени,
w = df/dt
и направленный вдоль оси вращения таким образом, чтобы из его конца вращение тела было видно происходящим против часовой стрелки. Направление вектора w совпадает с направлением поступательного движения буравчика, рукоятка которого вращается вместе с телом.
Вектор углового ускорения - первая производная вектора угловой скорости:
|
|
(2.23) |
Вектор углового ускорения тела равен первой производной вектора угловой скорости и характеризует изменение угловой скорости по величине и направлению.
Угловой скоростью называют векторную величину, характеризующую быстроту вращения твердого тела, определяемую как приращение угла поворота тела за промежуток времени.
Вектор угловой скорости ω может быть приложен к любой точке мгновенной оси и направлен в каждый момент времени по мгновенной оси Ω, так, чтобы, смотря навстречу этому вектору, видеть вращение тела происходящим против движения часовой
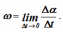

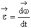 .
.