26. Потенциальное векторное поле. Нахождение потенциала.

Векторное поле потенциальное, если существует скалярная ф-я 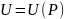такая, что 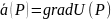для любого . 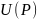– потенциал векторного поля.

В пространстве , где

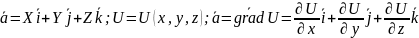
Теорема. Если вект поле потенциально в области V, то его потенциал определяется с точностью до константы.

Пусть 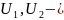потенциалы, тогда 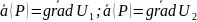следовательно:

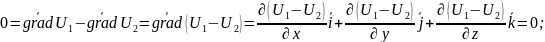
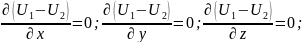отсюда:

Если векторное поле задано в односвязной области V, то необходимым и достаточным условием потенциальности поля является обращение в 0 ротора поля в точке .

Если 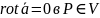, то поле потенциально.

26. Соленоидальное и гармоническое векторные поля и их простейшие свойства.

Соленоидальное. наз соленоидальным, если

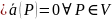
Свойства:

1. Если поле соленоидально, то поток соленоид вект поля через любую замкнутую пов-тьQ равен 0:

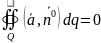
2. П отоки соленоид вект поля через различные сечения вект трубки равны между собой – принцип сохранения интенсивности вект трубки.

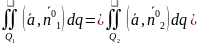
Гармоническое. Вект поле назыв гармоническим, если оно явл и соленоидальным, и потенциальным, т.е

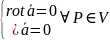
Если поле потенциально, то сущ потенциал U(P) тогда

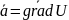
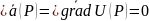
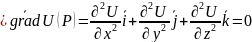
26. Числовые ряды. Сходимость и сумма рядов. Простейшие свойства рядов. Необходимое условие сходимости числового ряда.

Рассм послед-ть чисел

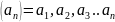
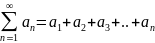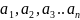(1) - числовой ряд, где – члены ряда. 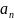– общий член ряда. 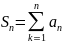– частичная сумма n-членов ряда.

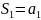
Определение. Если для послед-ти сущ конечный предел 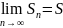, то ряд (1) сходится и его сумма равна S. 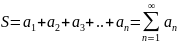Если предел послед-ти частичных сумм не существует либо равен бесконечности, то ряд (1) расходящийся.

Свойства:

1. Перестановка, добавление или убирание конечного числа членов ряда не влияет на сходимость или расходимость ряда.

2. Пусть ряды 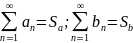сходятся. Тогда 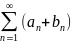сходится ; .

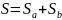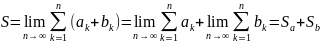Необходимый признак сходимости.

Теорема. Если ряд 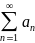сходится, то 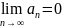; – предел частичных сумм равен числу.

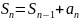
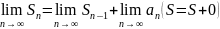Т.о. . Следствие: если 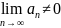, то ряд расходится.

Теорема. Чтобы ряд сходился, необходимо и достаточно, чтобы послед-ть его частичных сумм была ограничена. Если ряд сходится, то существует предел конечных сумм т.е. частичные суммы ограничены. Если ( ) ограничена, то ее предел 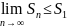не превосходит какого-то числа 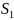т.е. ряд сходится.

26. (+36+37+38) Ряды с положительными слагаемыми. Интегральный признак (+признак сравнения+ признак Даламбера + признак Коши)

Рассмотрим ряд 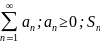не убывает.

1. Интегральный признак Коши.

Теорема. Если неотрицательная интегрируемая на промежутке ф-я f(x) монотонно убывает f(x)≥0, а ряд такой, что 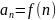, то ряд и 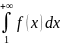сходятся и расходятся одновременно, причем в случае сходимости справедливо неравенство: .

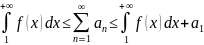2. Признак сравнения.

Пусть есть и с неотр членами. При этом 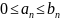для 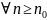. Тогда из сходимости ряда следует сходимость , а из расходимости следует расходимость .

3. Признак Даламбера.

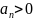Если сущ 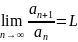, то при: Исп свойство предела. Если для 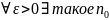, что .

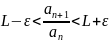4. Признак Коши.

Если для ряда существует предел 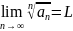, то, если: