
- •Свойства интегралов по фигуре от скалярных функций.
- •Применение интегралов по фигуре от скалярной функции в геометрии.
- •Криволинейный интеграл 1 рода. Определение и простейшие свойства.
- •Вычисление криволинейного интеграла 1-го рода по кривой на плоскости в зависимости от способа задания кривой.
- •Вычисление криволинейного интеграла 1-го рода по кривой в пространстве.
- •Приложения криволинейного интеграла 1-го рода в механике и геометрии.
- •Поверхностный интеграл 1-го рода. Определение и простейшие свойства этого интеграла.
- •Вычисление поверхностного интеграла 1-го рода сведеением к двойному интегралу.
- •Приложения поверхностного интеграла 1-го рода в механике.
- •Интеграл по ориентированной фигуре от векторной функции. Теорема существования. Простейшие свойства.
- •Независимость криволинейного интеграла 2-го рода от пути интегрирования (случай плоской кривой). Нахождение ф-ии по ее полному дифференциалу.
- •Двойной интеграл. Определение, геометрический сымсл двойного интеграла.
- •Свойства двойного интеграла.
- •Вычисление двойного интеграла в декартовых координатах.
- •Приложения двойного интеграла в механике.
- •Тройной интеграл. Определение и простейшие свойства тройного интеграла.
- •В ычисление тройного интеграла в декартовых координатах. Приложения тройного интеграла в геометрии.
- •Тройной интеграл в сферических координатах.
- •Тройной интеграл в цилиндрических координатах.
- •Приложения тройного интеграла в механике.
- •Скалярное поле. Поверхности и линии уровня скалярного поля.
- •Производная по направлению. Градиент.
- •Векторное поле. Векторные линии и их уравнения.
- •Поток, дивергенция векторного поля. Теорема Остроградского-Гаусса.
- •Циркуляция и ротор векторного поля. Теорема Стокса.
- •Потенциальное векторное поле. Нахождение потенциала.
- •Соленоидальное и гармоническое векторные поля и их простейшие свойства.
- •Числовые ряды. Сходимость и сумма рядов. Простейшие свойства рядов. Необходимое условие сходимости числового ряда.
- •Знакопеременные ряды. Достаточный признак сходимости. Абсолютная и условная сходимости.
- •Знакочередующиеся ряды. Теорема Лейбница. Оценка остатка ряда.
- •Ряды с комплекными членами.
- •Функциональные ряды. Область сходимости. Понятие ранвомерной сходимости. Признак Вейерштрасса.
- •Свойства равномерно сходящихся функциональных рядов.
- •Степенные ряды. Теорема Абеля. Радиус сходимости. Интервал сходимости.
Тройной интеграл. Определение и простейшие свойства тройного интеграла.
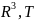 -
ограниченное тело. Пусть f(M)
непрерывна на области T,
-
ограниченное тело. Пусть f(M)
непрерывна на области T,
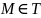
Разобъем
T
на
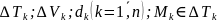
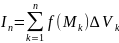
Если предел интегральных сумм существует при условии и этот предел не зависит от способа разбиения области на элементарные подобласти и от выбора точек в этих областях, то такой предел – тройной интеграл.
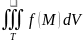
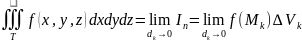
Если f(M) непрерынва по области Т, то тройной интеграл существует.
Свойства:
пусть
интегрируемы на Т. пусть
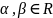
Линейность.
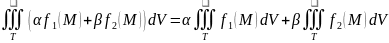
Аддитивность. Если
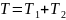 ;
;
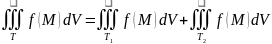
Если
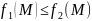 для любых
для любых
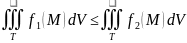
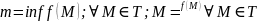 ;
;
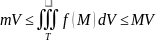 ;
V
– объем T.
;
V
– объем T.
Теорема о среднем. Сущ
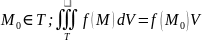
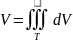
Если - плотность, то
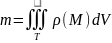
В ычисление тройного интеграла в декартовых координатах. Приложения тройного интеграла в геометрии.
Пусть
областью интегрирования Т явл тело,
ограниченное снизу пов-тью
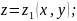 сверху
-
сверху
-
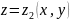 причем
причем
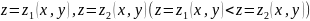 – непрерывные ф-ии в замкнутой области
D,
овляющейся проекцией тела на плоскость
Oxy.
Считаем Т правильной в направлении оси
Oz.
Тогда:
– непрерывные ф-ии в замкнутой области
D,
овляющейся проекцией тела на плоскость
Oxy.
Считаем Т правильной в направлении оси
Oz.
Тогда:
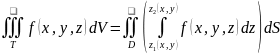 .
.
Е
сли
область D
ограничена линиями x=a,
x=b
(a<b),
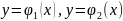 где
где
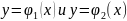 -
непрерывные на отрезке [a,b]
ф-ии, причем
-
непрерывные на отрезке [a,b]
ф-ии, причем
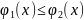 ,
то:
,
то:
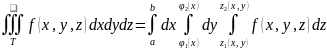
Приложения тройного интеграла.
Объем тела.
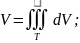
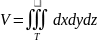 -в
декартовых координатах
-в
декартовых координатах
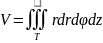 -
в цилиндрических
-
в цилиндрических
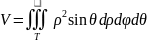 -
в сферических
-
в сферических
Тройной интеграл в сферических координатах.
С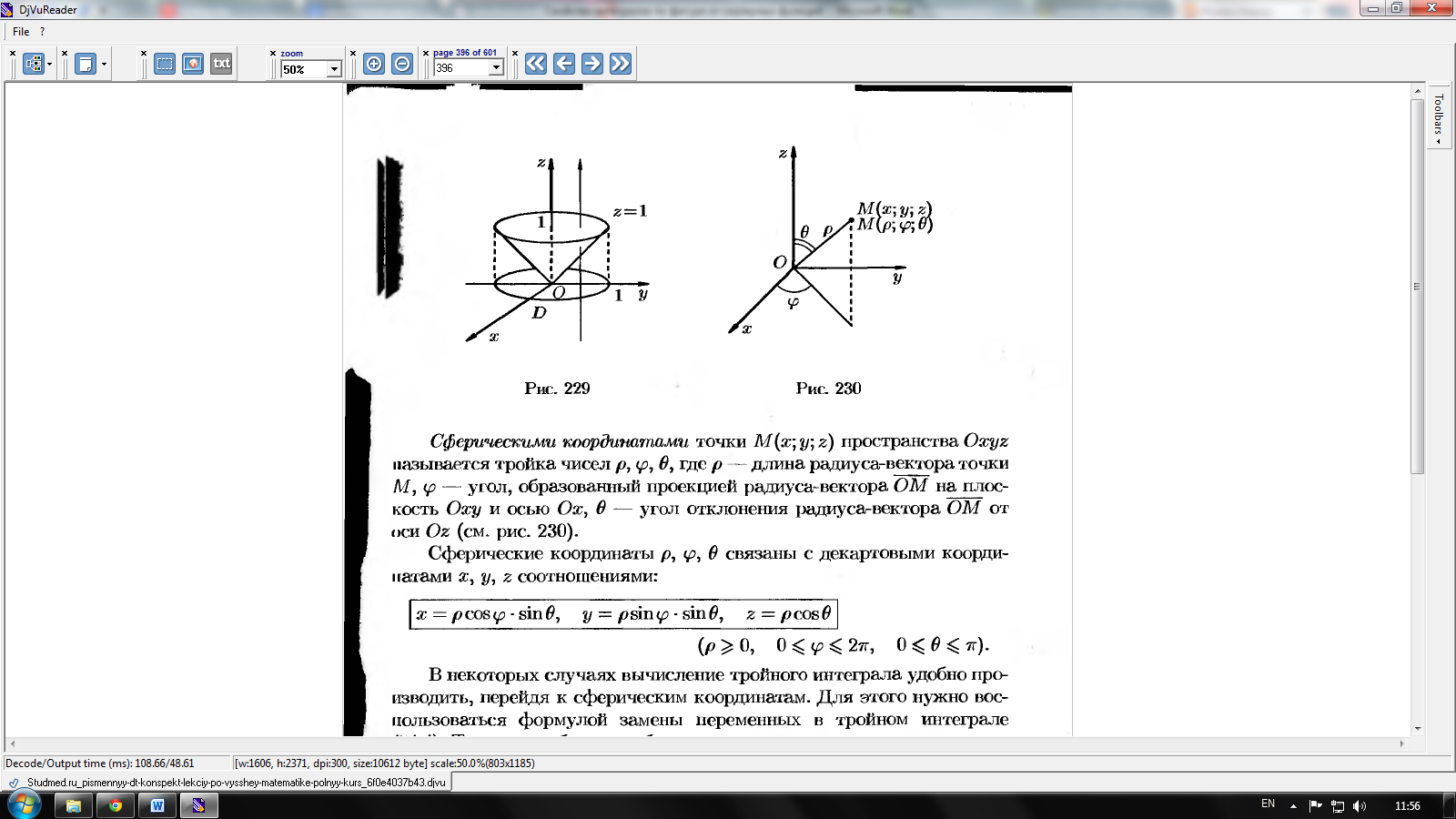 ферическими
координатами точки M(x,y,z)
пространства Oxyz
называется тройка чисел
ферическими
координатами точки M(x,y,z)
пространства Oxyz
называется тройка чисел
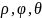 ,
где
,
где
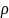 – длина радиус-вектора точки М,
– длина радиус-вектора точки М,
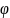 – угол, образованный проекцией
радиуса-вектора
– угол, образованный проекцией
радиуса-вектора
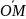 на плоскость Oxy
и осью Ox,
на плоскость Oxy
и осью Ox,
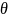 -
угол отклонения радиуса-вектора
от оси Oz.
Сферические координаты
связаны с декартовыми координатами
x,y,z
соотношениями:
-
угол отклонения радиуса-вектора
от оси Oz.
Сферические координаты
связаны с декартовыми координатами
x,y,z
соотношениями:
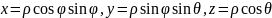 ;
;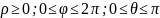
Для перехода к сферическим координатам нужно воспользоваться формулой замены переменных в тройном интеграле. Т.к. якобиан преобразования:
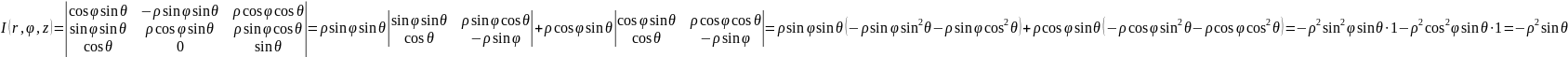
То
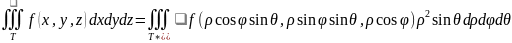
Тройной интеграл в цилиндрических координатах.
П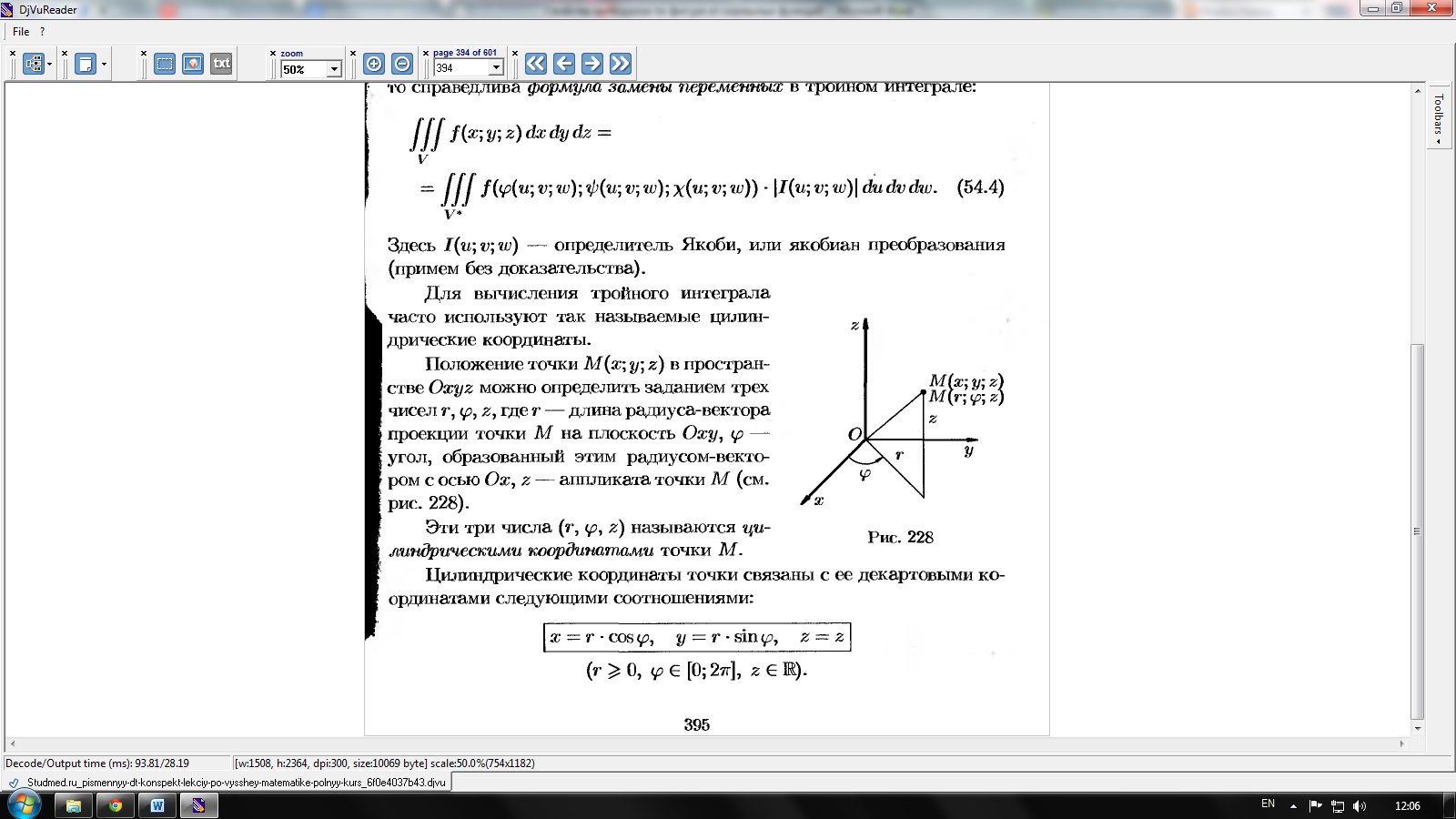 оложение
точки M(x,y,z)
в пространстве Oxyz
можно определить заданием трех чисел
оложение
точки M(x,y,z)
в пространстве Oxyz
можно определить заданием трех чисел
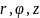 ,
где
,
где
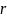 – длина радиуса-вектора проекции точки
М на плоскость Oxy,
-
угол, образованный этим радиусом-вектором
с осью Ox,
– длина радиуса-вектора проекции точки
М на плоскость Oxy,
-
угол, образованный этим радиусом-вектором
с осью Ox,
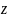 -
аппликата точки М.
-
аппликата точки М.
Эти три числа называют цилиндрическими координатами точки М. цилиндрические координаты точки связаны с ее декартовыми координатами следующими соотношениями:
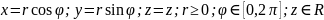
Возьмем в качестве u,v,w цилиндрические координаты и вычислим якобиан преобразования:

Формула замены переменных:
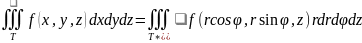
Приложения тройного интеграла в механике.
Масса
тела. При заданной объемной плотности
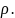
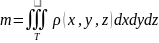
 -
объемная плотность распределения массы
в точке M(x,y,z)
-
объемная плотность распределения массы
в точке M(x,y,z)
Статические
моменты. Моменты
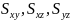 тела относительно координатных плоскостей
Oxy,
Oxz,
Oyz
вычисляются по формулам:
тела относительно координатных плоскостей
Oxy,
Oxz,
Oyz
вычисляются по формулам:

Центр тяжести тела. Координаты центра тяжести тела Т находятся по формулам:
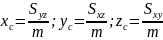
Скалярное поле. Поверхности и линии уровня скалярного поля.
Скалярное
поле – пространство
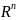 либо область
либо область
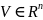 ,
где определена
,
где определена
 –
радиус-вектор точки Р.
–
радиус-вектор точки Р.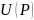 – потенциал скалярного поля.
– потенциал скалярного поля.
Основные характеристики: поверхности (линии) уровня, производная по направлению, градиент.
Поверхность
уровня – множество точек, в каждой из
точек
потенциалы сохраняют постоянное
значение.
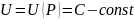
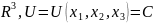 – поверхность
уровня
– поверхность
уровня
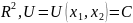 – линия
уровня – линия на плоскости Oxy,
в точках которой функция
– линия
уровня – линия на плоскости Oxy,
в точках которой функция
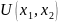 сохраняет постоянное значение.
сохраняет постоянное значение.
