27. Які властивості архітектурної форми можуть бути узгоджені шляхом застосуванням систем пропорціювання.

Дуже важливо, щоб система пропорціональності була єдиною для всього архітектурного організму, включаючи всі його параметри і навіть елементи внутрішнього і зовнішнього благоустрою. У цьому випадку цілісність сприйняття споруди посилюється, і воно набуває художню завершеність.

Пропорціональність - це використання пропорцій для організації елементів форми в цілісну структуру, тобто застосування певного методу кількісного узгодження частин і цілого. Застосування пропорцій в архітектурі стародавнього світу було тісно пов'язане з характером будівельного виробництва і способами вимірювання. Необхідність нанесення контурів майбутньої будівлі на землі і креслення його плану в натуральну величину сприяли розвитку стійких прийомів побудови геометричних фігур і вироблення певних пропорційних відносин для взаємозв'язку їх габаритів.

2 8. Охарактеризувати модульні системи пропорціонування. Навести приклад мод сист пропорц-ня.

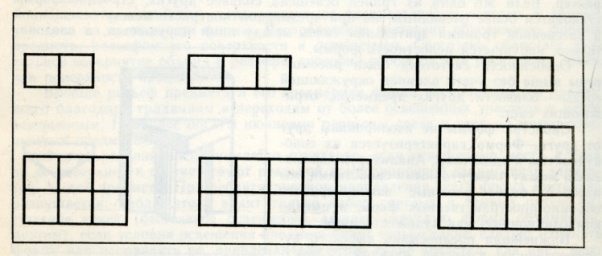
на отношении 1:1 строятся простейшие геометрические формы квадрат, куб. Отношения 1:2, 1:3, 1:4, 1:5, 1:6 в прямоугольной форме дают повторение квадрата целое число раз. Отношения 2:3, 2:5, 3:4, 3:5, 5:6 содержат в себе модуль, укладывающийся целое число раз в каждой геометрической величине, входящей в данное отношение.

29. Охарактеризувати ірраціональні системи пропорціонування. Навести приклад ірраціональні системи пропорціонування. Основаны на иррациональных отношениях и не могут быть выражены целым числом.

иррациональные отношения:

1. отношение диагонали квадрата к его стороне 1:√2;рис 26А

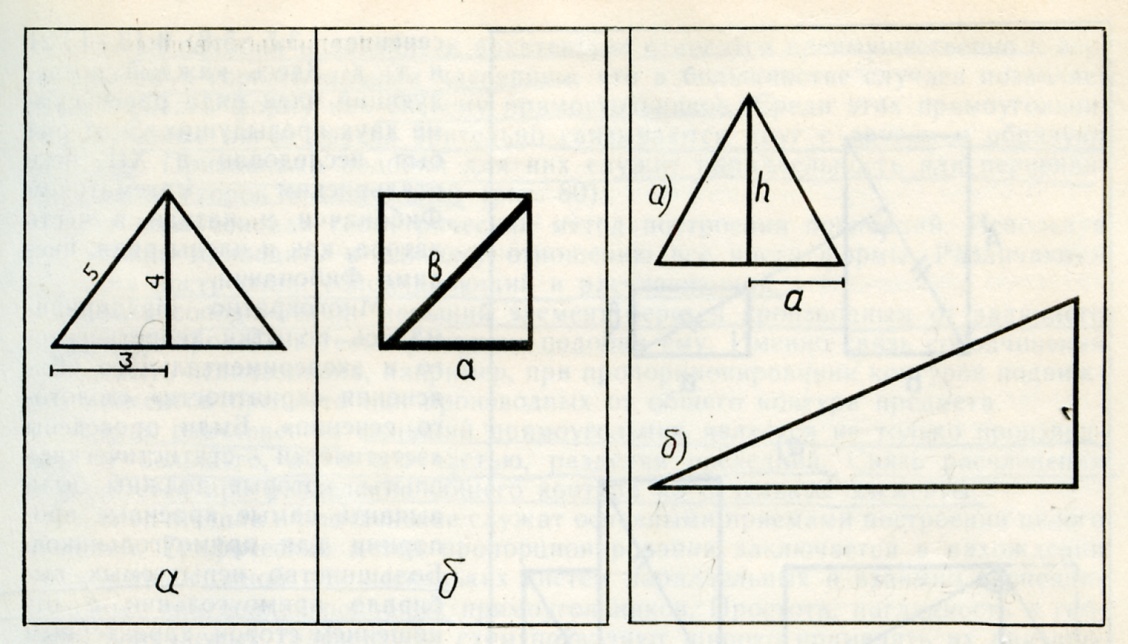
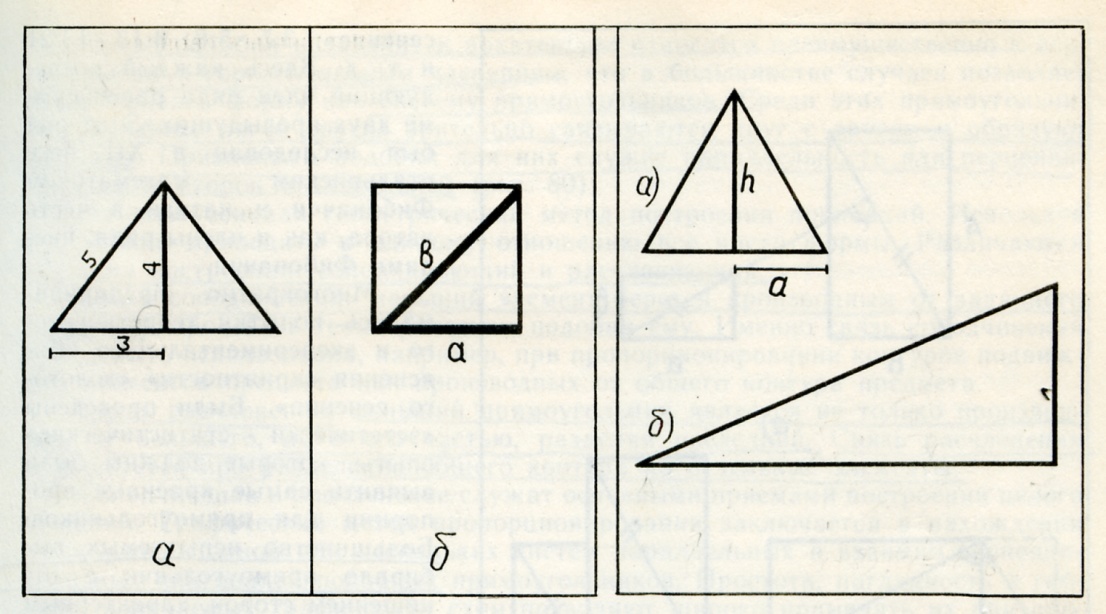
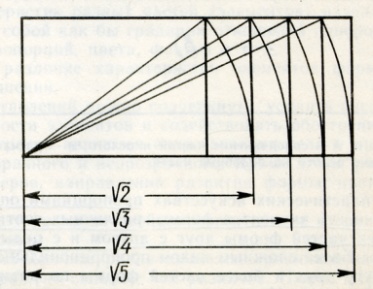
26А 26Б 26В

2. отношение высоты равнобедренного треугольника к половине его основания 1: √3; рис 26Б

3. динамический ряд прямоугольников (рис 26в)

4. «золотое сечение», которое выражается дробным числом 1:1,62 (27А) эта пропорция была известна и в античности. При раскопках в Помпеях был найден пропорциональный циркуль, закрепленный на золотом сечении (27Б).

30. Охарактеризувати графічні та арифметичні способи побудови систем пропорціонування. Навести приклади графіч-го та ариф-го способів побудови систем проп-ня.

Графічний- за допомогою креслярських інструментів та олівця.

А рифметичні - розраховуються за допомогою чисел та арифметичних прийомів .

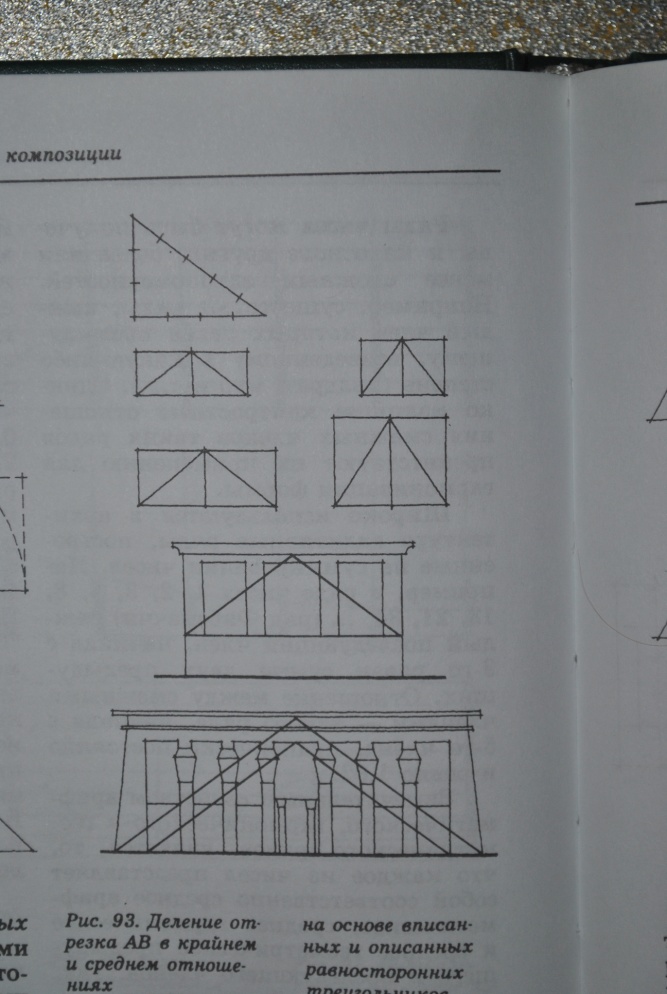
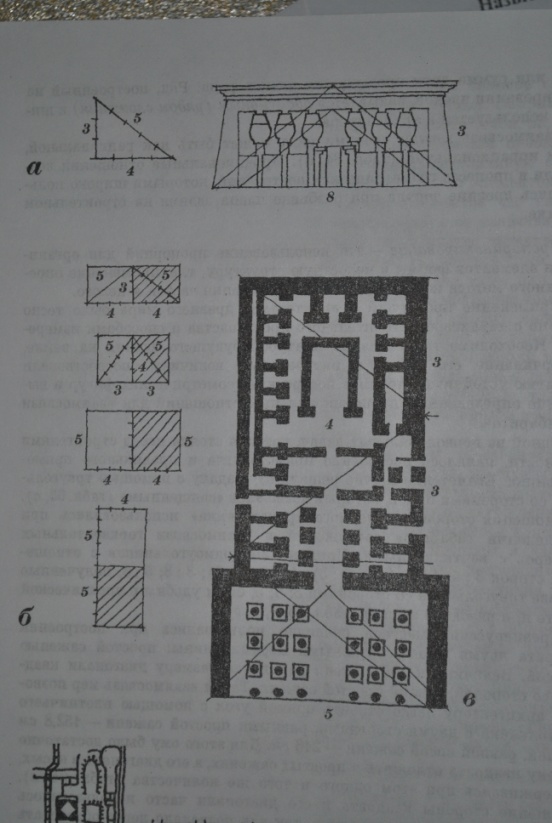
31. Принципи побудови і особливості використання системи пропорціонування на основі Єгипетського трикутника.

Система пропорціонування на основі єгипетського трикутника з співвідношенням сторін 3:4:5 дозволяє отримувати прямий кут та ряд прямокутників зв сторонами, виражених у простих цілих числах.

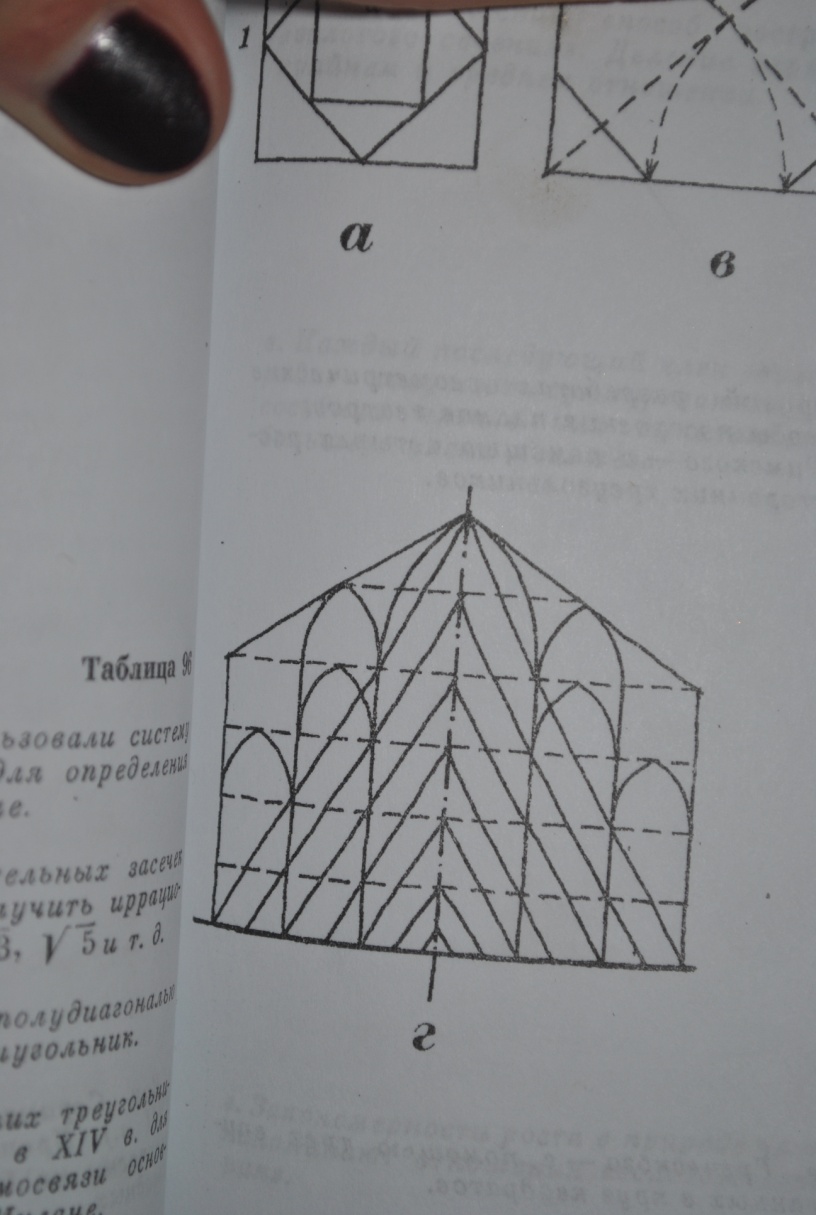
32. Принципи побудови і особливості використання системи пропорціонування на основі триангулювання.

Система рівносторонніх трикутників, покладена в основу пропорій, уявляла собой арифметичний ряд:√3, 2√3, 3√3,4√3 …

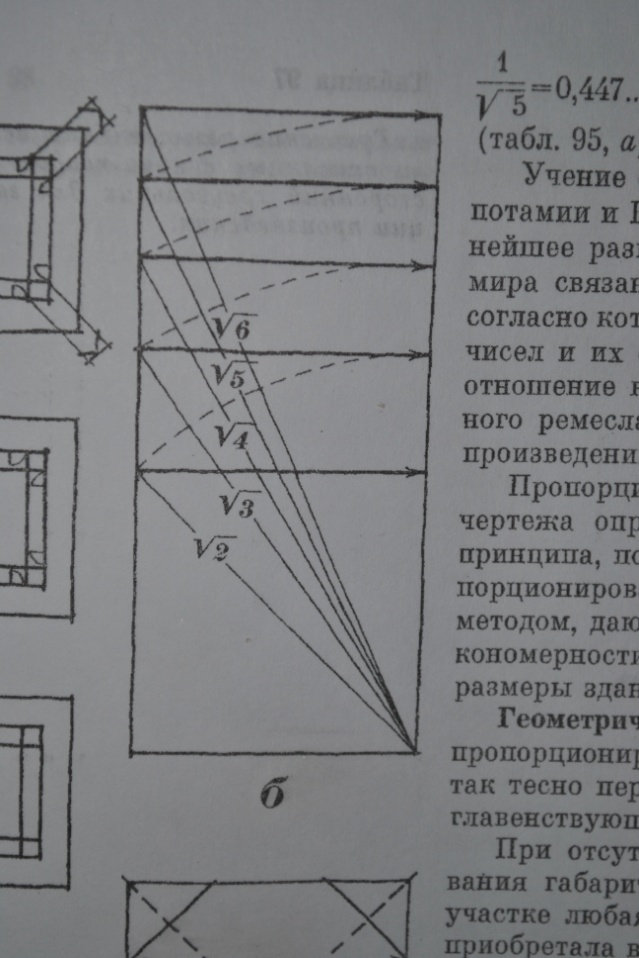
33. Принципи побудови і особливості використання системи пропорціонування на основі співвідношення сторони і діагоналі квадрата. Співвідношення сторони квадрата до діагоналі дорівнює 1: √2. Для побудови використовується спосіб засічки діагоналлю квадрата на продовжену лінію його сторони. Послідовною побудовою прямокутників на основі квадарата зі сталою шириною та довжиною,яка дорівнює діагоналі, можна отримувати іраціональні числа: √2, √3, √5, √6 і т.д.

34)

Система пропорционирования равносторонних треугольников

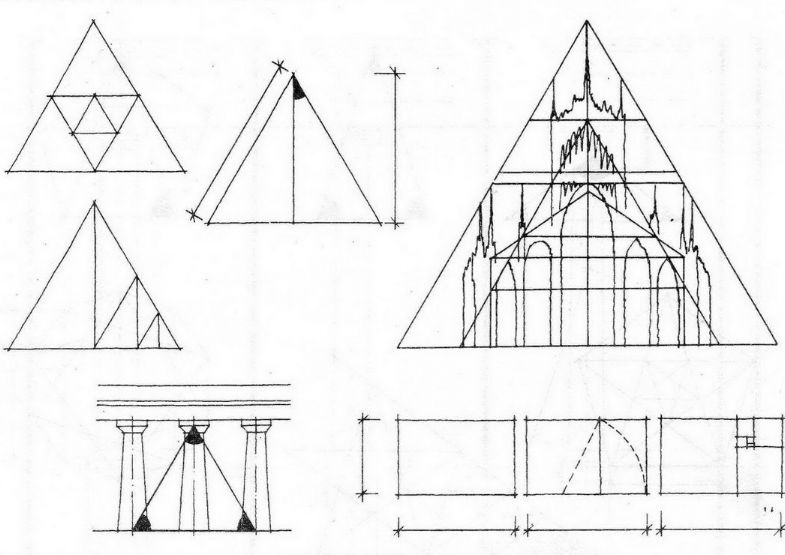
Система вписанных равносто­ронних треугольников дает ряд на основе двух чередующихся отноше­ний: стороны треугольника к высо­те (2/ V 3) и высоты к половине сто­роны (v'a) . Пропорциониро-вание на основе равностороннего треугольника особенно широко при­менялось в средневековье» где сис­тема триангулирования пронизыва­ла всю структуру готических собо­ров (рис.97), однако отношения, свойственные этой системе, могут быть обнаружены и в архитектуре других эпох, например, в архитек­туре Древней Греции.

3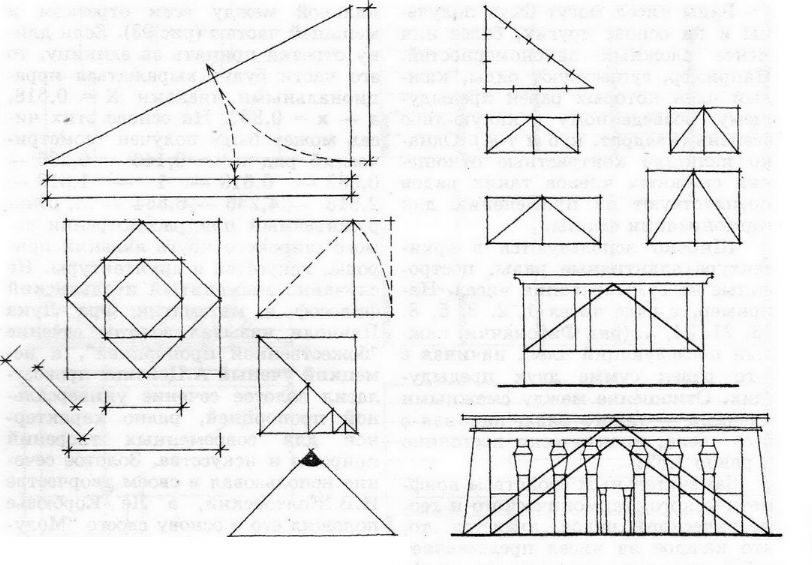 5)

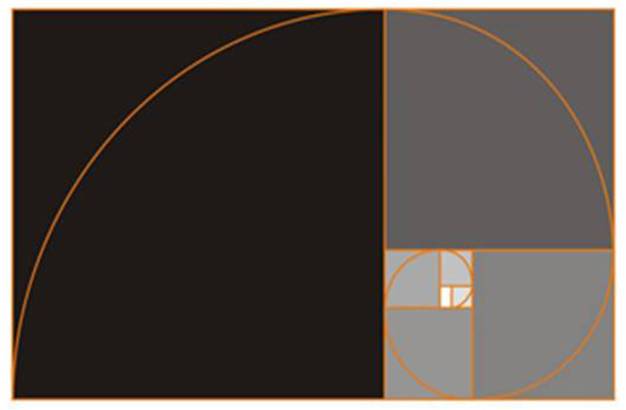золотая логарифмическая спираль

36) Наиболее известным и в то же время загадочным рядом средних чисел является так называемое от­ношение золотого сечения. Термин "золотое сечение" был введен Лео­нардо да Винчи для известного еще пифагорейцам описанного Эвкли- дом деления отрезка в так называе­мом "крайнем и среднем отноше­нии", при котором большая его часть является средней пропорцио­нальной между всем отрезком и меньшей частью .Если дли­ну отрезка принять за единицу, то его части будут выражаться ирра­циональными числами X = 0,618, а — х = 0,382. На основе этих чи­сел может быть получен геометри­ческий ряд ... — 0,146 — 0,236 — 0,382 — 0,618 — 1 — 1,618 — 2,618 — 4,236 — 6,854 — ..., обна­руживаемый при рассмотрении са­мого широкого круга явлений при­роды, искусства и архитектуры. Не случайно знаменитый итальянский философ и математик Фра Лука Паччоли называл золотое сечение "божественной пропорцией", а не­мецкий ученый А.Цейзинг провозг­ласил золотое сечение универсаль­ной пропорцией, равно характер­ной для современных творений природы и искусства. Золотое сече­ние использовал в своем творчестве И.В.Жолтовский, а Ле Корбюзье положил его в основу своего "Моду- лора".

Золотое сечение выражают обычно числом 1,618 или обратным ему числом 0,618, для которых по предложению Т.Куба и М.Бара приняты символы Ф и 1/Ф. Эти числа являются знаменателями - возрастающего (Ф) и убывающего, (l/Ф) рядов золотого сечения.ч Ин­тересной особенностью этих чисел является их способность при сложе­нии с единицей (для Ф) и при вы­читании из единицы , (для 1/Ф) да­вать квадраты самих себя, т.е. 1 + Ф + Ф²; 1 — 1/Ф = (1/Ф)². Золотое сечение — это единственная геомет­рическая прогрессия, обладающая признаком аддитивного ряда (Ф₃ = Ф₁ + Ф₂).

Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении) — деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине. Отношение большей части к меньшей в этой пропорции выражается квадратичной иррациональностью

и, наоборот, отношение меньшей части к большей

Число   называется также золотым числом.

37.Настя ГР

38.Настя ГР.

39.Настя ГР.

40 Посліідовність Фібоніччі

Послідо́вність Фібона́ччі, чи́сла Фібона́ччі — числова послідовність   задана рекурентним співвідношенням другого порядку

і т.д. Ця послідовність виникає у найрізноманітніших математичних ситуаціях - комбінаторних, числових, геометричних.

В природі числа Фібоначчі часто трапляються в різних спіральних формах. Так, черешки листя примикають до стебла по спіралі, що проходить між двома сусідніми листками: 1/3 повного оберту в ліщини, 2/5 - у дуба, 3/8 - у тополі і груші, 5/13 - у верби; лусочки на ялиновій шишці, насіння соняшника розташовані спіралями, причому кількості спіралей кожного напрямку також, як правило, числа Фібоначчі.

Числа Фібоначчі щільно пов'язані з золотим перетином 

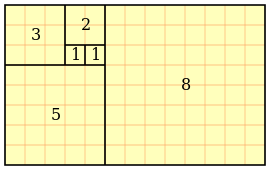
Ідея полягає в наступному.

F_n = F_(n-1) + F_(n-2)

F_(n+1) = F_n + F_(n-1) = 2*F_(n-1) + F_(n-2)

Покладемо F₀ = 0, при цьому співвідношення при n = 2 залишиться істинним. Таким чином утворюється послідовність

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ..

41

За свідченням Месселя, античні зодчі в якості джерела гармонії архітектурних будівель незмінно використовували геометричні проекції п'яти так званих «Платонових тіл», що відображають відповідно до їхніх представлень загальну гармонію світу. Це вписані в сферу правильні багатогранники з числом граней 4, 6, 8, 12, 20.

Е. Мессель, зокрема, особливо виділяє пропорції, засновані на вписаному в коло правильному десятіугольніке. Ставлення радіусу кола до сторони багатокутника виражається ірраціональним числом (√ 5 +1) / 2 = 1,61 8 і дає пропорцію так званого «золотого перетину».