
- •Тема 1. Классификация дифференциальных уравнений второго порядка в частных производных.
- •1.1 Линейное дифференциальное уравнение второго порядка в частных производных.
- •1.2 Три типа дифференциальных уравнений второго порядка в частных производных
- •1.3 Характеристические уравнения для дифференциальных уравнений второго порядка
- •1.4 Приведение дифференциальных уравнений второго порядка к каноническому виду
- •1.5 Каноническая форма дифференциальных уравнений второго порядка с постоянными коэффициентами.
- •1.6 Каноническая форма ду со многими переменными
- •Тема 2. Краевые задачи гиперболического типа
- •2.1 Уравнения малых поперечных колебаний упругой струны.
- •2.2. Малые продольные колебания упругого стержня
- •2.3. Малые поперечные колебания упругой мембраны
- •2.4. Электромагнитное поле в однородных средах
- •2.5. Постановка краевых задач и их редукция
- •2.6. Свободные колебания бесконечной струны (стержня)
- •2.7. Свободные колебания полубесконечной струны (стержня)
- •2.8. Свободные колебания струны ограниченных размеров
- •2.9. Вынужденные колебания бесконечной струны
- •2.10. Распространение сферически симметричных волн в пространстве.
- •2.12. Возникновение стоячих волн и их суперпозиция
- •2.13. Связь формулы Даламбера с решением в виде рядов Фурье
- •2.14 . Решение неоднородной краевой задачи методом разделения переменных.
- •2.16. Формула Римана для вынужденных колебаний бесконечной струны
- •2.16. Формула Римана для колебаний полубесконечной струны
- •2.17. Существование и единственность краевых задач гиперболического типа
- •Тема 3. Краевые задачи параболического типа.
- •3.1O Уравнение теплопроводности
- •3.2O Охлаждение бесконечного стержня. Формула Пуассона.
- •3.3O Охлаждение полубесконечного стержня и стержня ограниченных размеров.
- •3. . Решение неоднородной краевой задачи теплопроводности.
- •3. . Решение однородной краевой задачи теплопроводности методом разделения переменных.
- •3. . Решение неоднородной краевой задачи теплопроводности методом разделения переменных.
- •3. . Связь формулы Пуассона с решением методом разделения переменныx.
- •3. Теорема об экстремуме и её следствия.
- •3. . Существование, единственность и корректность решений краевых задач теплопроводности.
- •Тема IV.Краевые задачи эллиптического типа.
- •4. Физические процессы, порождающие уравнения эллиптического типа.
- •4. Решение одномерных уравнений Пуассона и Лапласа.
- •4. Решение двумерных уравнений Лапласа методом разделенных переменных.
- •Математическое дополнение, формулы Грина.
- •4. Решение трехмерных уравнений Пуассона и Лапласа в общем случае.
- •4. Общее решение уравнения Лапласа при наличии разрыва производной искомой функции.
- •4. Общее решение уравнения Пуассона в двумерном случае. Математическое дополнение.
- •Тема 5. Специальные функции.
- •5.10 Гармонические колебания круглой мембраны.
- •5.20 Функции Бесселя
- •5.30 Рекуррентные формулы для функций Бесселя.
- •5.40 Интегральные представления цилиндрических функций.
- •5.50 Гармонические колебания сферы.
- •5.60 Сферические функции.
- •5.7 Полиномы Лежандра.
- •5.80 Полиномы Чебышева-Эрмита и Чебышева - Лагерра.
Тема 2. Краевые задачи гиперболического типа
2.1 Уравнения малых поперечных колебаний упругой струны.
У нас есть некая гибкая струна, которая колеблется (Рис.4).
Рис.4 |
В каждый момент
времени струна имеет профиль
|
Введем некоторые ограничения.
а)
 (поперечность).
(поперечность).
Поперечные
колебания реализуются перпендикулярно
направлению оси
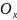 и лежат в одной плоскости. В положении
равновесия струна лежит на оси
.
Сила внешнего воздействия тоже
перпендикулярна направлению оси
.
и лежат в одной плоскости. В положении
равновесия струна лежит на оси
.
Сила внешнего воздействия тоже
перпендикулярна направлению оси
.
б)
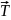 (сила упругости) является касательной
к профилю струны и ее величина мало
меняется со временем
(сила упругости) является касательной
к профилю струны и ее величина мало
меняется со временем
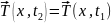 (Рис.5)
(Рис.5)

Рис.5
в) Колебания малы, т.е. нет растяжения участков струны (участки струны практически не меняют свою длину).
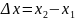
Длина
дуги
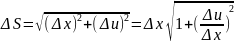
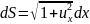
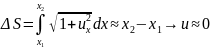 ,
где
,
где
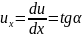
Условие малости колебанийф
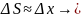
Выпишем
проекции векторов
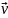 и
на оси:
и
на оси:
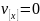 ,
,
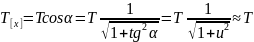 ;
;
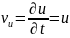 ,
,
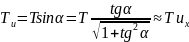
Пусть
m – массы струны длиной
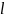 .
.
Введем
линейную плотность массы
 .
.
Если
струна однородна, то
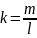 . Участок струны dx
с dm = k dx
движется со скоростью
. Участок струны dx
с dm = k dx
движется со скоростью
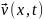 .
.
Для участков dx и ∆x получаем изменение импульса
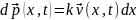 ,
,
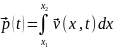 .
.
Теперь
используем второй закон Ньютона:
 ,
,
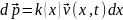 ,
,
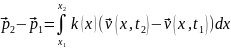
Определим силу, силу действующую на участок струны
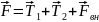 ,
где
,
где
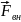 - внешняя сила.
- внешняя сила.
Пусть
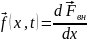 и
и
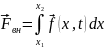 .
.
Сила
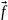 перпендикулярна к оси
,
т.е.
перпендикулярна к оси
,
т.е.
 ,
,
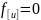 .
.
Тогда второй закон Ньютона примет вид векторного равенства

Получаем
проекцию векторного равенства на ось
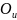
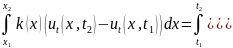
Проекция этого равенства на ось может быть сведена к векторному равенству
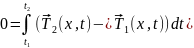
Интеграл
не зависит от
,
и нет зависимости
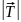 от
.
от
.
В итоге
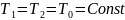
Получаем интегральное уравнение колебаний струны.

Чтобы привести интегральное уравнение к дифференциальному, нужно воспользоваться теоремой о среднем, которая гласит
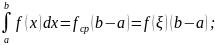
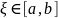 .
.
Тогда

где
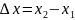 ;
;
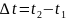 ;
;
 ;
;
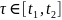 .
.
После
деления на
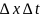 получим
получим
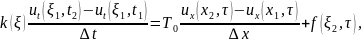
после предельного перехода
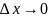 ,
,
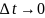 ,
,
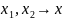 ,
,
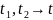 ,
,
 ,
,
 ;
;
получаем дифференциальное уравнение со вторыми производными
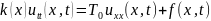
или
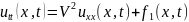 ; (2.1)
; (2.1)
где
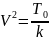 ,
,
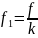 .
.
Для однородной струны коэффициент – постоянен.
Уравнение (2.1) описывает малые колебания струны.
Физический
смысл
 определим из соображений размерности:
определим из соображений размерности:
 ,
,
следовательно,
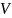 является скоростью, не совпадающей со
скоростью струны. Ее смысл будет
установлен в дальнейшем.
является скоростью, не совпадающей со
скоростью струны. Ее смысл будет
установлен в дальнейшем.
Покажем, что (2.1) - уравнение гиперболического типа.
Определим
дискриминант
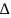 для (2.1). Сравнивая с (1.1), получаем
для (2.1). Сравнивая с (1.1), получаем
 ,
,
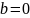 ,
,
 ,
из этого следует
,
из этого следует
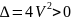 .
.
Следовательно (2.1) является уравнением гиперболического типа.
2.2. Малые продольные колебания упругого стержня
Под действием внешних сил стержень начинает колебаться.
Искомая
функция
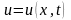 – величина смещения к моменту времени
t
точки, имевшей в положении равновесия
координату х.
– величина смещения к моменту времени
t
точки, имевшей в положении равновесия
координату х.
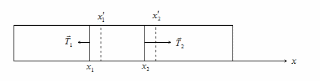
Рис. 6.
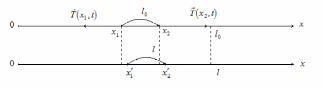
Рис. 7.
Рассмотрим некоторые ограничения:
 колебания
точек стержня совершаются вдоль оси
колебания
точек стержня совершаются вдоль оси
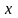 ,
т.е. v=vx,
T=Tx,
F=Fx;
,
т.е. v=vx,
T=Tx,
F=Fx;
 работает
закон Гука, причем
работает
закон Гука, причем
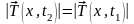 ;
;
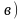 колебания
малы
колебания
малы
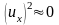 (по аналогии с 2.1).
(по аналогии с 2.1).
Введем характеристики деформации.
Если
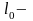 длина отрезка
длина отрезка
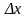 в
положении равновесия, а
в
положении равновесия, а
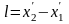 – его длина в смещенном положении, тогда
– его длина в смещенном положении, тогда
 –
абсолютное удлинение отрезка, а
–
абсолютное удлинение отрезка, а
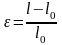 – его относительное удлинение.
– его относительное удлинение.
Пусть
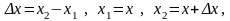
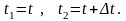
При
рассмотрении данного участка, его начало
–
 переходит в
переходит в
 ,
а его конец –
,
а его конец –
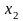 переходит в
переходит в
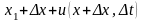 ,
тогда
,
тогда
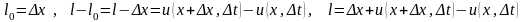 ,
,
Относительное удлинение примет вид
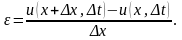
Если
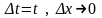 ,
получаем:
,
получаем:
Силу натяжения по закону Гука представим как
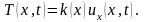
Будем пользоваться вторым законом Ньютона:
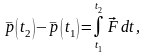 где
где
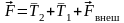 ,
а
,
а
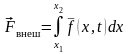 .
.
Введем линейную плотность массы
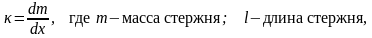
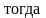
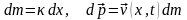 .
.
Если
стержень однороден, то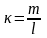 .
Запишем изменение импульса
.
Запишем изменение импульса
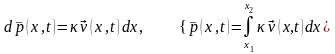 ,
,
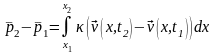 .
.
В
нашем случае
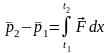 .
.
Импульс силы равен
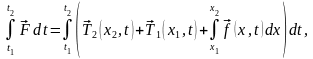 тогда
по второму закону Ньютона получаем
тогда
по второму закону Ньютона получаем
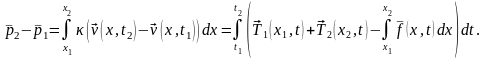
Легко
видеть, что v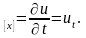
Проекция
векторного равенства на ось
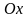 дает
дает
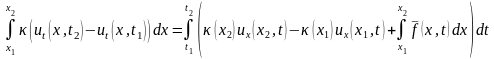 .
.
Воспользуемся теоремой о среднем, получим

Делим последнее равенство на ∆х∆t, устремляем ∆х и ∆t к нулю
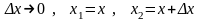 ,
,
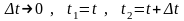 ,
,
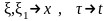
и получаем уравнение
 .
(2.2)
.
(2.2)
Пусть
 – константа, т.е. не зависит от x,
тогда уравнение (2.2) примет вид
– константа, т.е. не зависит от x,
тогда уравнение (2.2) примет вид
 .
.
Если
ввести величины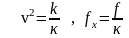 ,
то получим
,
то получим
 (2.2’)
(2.2’)
(2.2’) – уравнение продольных колебаний стержня, которое совпадает с уравнением для поперечных колебаний струны; т.е. 2 разных математических процесса описываются одинаково.

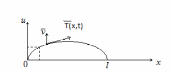
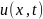 – смещение точки с координатами
к моменту времени
– смещение точки с координатами
к моменту времени
 .
.