28.Построение натуральной величи­ны сечения пирамиды плоскостью.

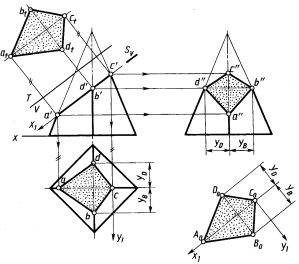
Во многих случаяхтребуется по­строить натуральный или истинный вид сечения тела плоскостью. На рисунке для этой цели вверху слева применен способ перемены плоскостей проекций. В качестве дополнительной плоскости принята плоскость T,параллельная плоскости Sи перпендикулярная плоскости V.Натуральный вид площадки – фигуры сечения a_tb_tc_td_t.Дру­гой вариант построения натурального вида наклонной пло­щадки ABCDпоказан на рисунке справа внизу – A₀B₀C₀D₀.Для построения использованы новые координатные оси x₁и у_1,лежащие в плоскости S.Ось х₁параллельна плоскости V, ось у₁перпендикулярна плоскости V.

Координаты на оси х₁точек A₀, B₀, C₀, D₀равны координа­там по оси x₁фронтальных проекций a', b', c', d' этих точек. Координаты х₁точек с₀, с' по оси х₁равны нулю. Координаты y_B, у_Dпо оси у₁точек B₀, D₀равны координатам по этой оси (параллельной оси у)горизонтальных проекций b, d.Коорди­наты по оси у₁точекА, С равны нулю. По указанным коорди­натам на осях x₁ , у₁строят натуральную величину A₀B₀C₀D_aнаклонной площадки ABCD.

29.Развертка поверхности пирамиды.

Построение развертки боковой поверхности пирамиды можно проводить в следующей последовательности:

определить длину ребер и сторон основания пирамиды;

выполнить чертеж развертки последовательным построени­ем треугольников – граней пирамиды.

Пример построения развертки поверхности треугольной пи­рамиды SABCприведен на рисунках.

Для удобства построения на рисунке 1 боковые ребра пирамиды продолже­ны до пересечения с плоскостью H.Это позволило определить на горизонтальной проекции длину отрезков 1– 2, 2– 3, 3– 4 нового основания пирамиды. Длина боковых ребер S–1, S–2, S–3 най­дена вращением их вокруг вертикальной оси– отрезки s'1'₁, s'2'₁, s'3'₁. Ha них найдены отрезки s'a'₁, s'b'₁, s'c'₁.По найденным отрезкам на рисунке 2 построена развертка боковой поверхно­сти S₀1₀2₀3₀1₀и затем S₀A₀B₀C₀A₀. Ha отрезке А₀С₀построе­на натуральная величина треугольника А₀В₀С₀по сторонам A₀B₀и С₀B₀, найденным способом прямоугольного треугольника.

30. Проекции цилиндра. Изображение цилиндра на чертеже. Точка и линия на поверхности цилиндра.

Цилиндром называется тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями.Часть цилиндрической поверхности, заключенной между плоскостями, называется боковой поверхностью, а части плоскостей, отсекаемые этой поверхностью, - основаниями цилиндра. Расстояние между плоскостями оснований есть высота цилиндра.По заданной фронтальной проекции А₂В₂ линии построим отсутствующие проекции.