21.Способ перемены плоскостей проекций.

Этот способ широко применяют в машиностроении и при­боростроении. Сущность способа перемены плоскостей проекций заключается в следующем: положение точек, линий, плоских фигур, поверхностей в пространстве не изменяется, а система V, H дополняется плоскостями, образующими с V, или H, или между собой системы двух взаимно перпендикулярных плоскостей, принимаемых за плоскости проекций. Каждая новая система выбирается так, чтобы по отношению к заданным геометрическим элементам она заняла положение, наиболее удобное для выполнения требуемого построения.

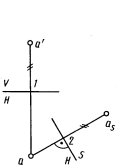
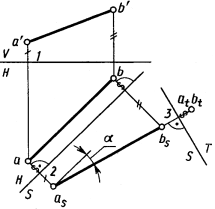
На рисунке 1 показано преобразование проекций точкиАиз системы V,Hв систему S, H, в которой вместо плоскости V введена новая плоскость S, а плоскость Hосталась неизмен­ной. При этом S H.В системе S,Hгоризонтальная проек­ция а точкиАосталась неизменной. Проекция a_sточкиАна плоскости Sнаходится от плоскости Hна том же расстоянии, что и проекция a' точки А на плоскости V.Это условие позво­ляет легко строить проекцию точки на чертеже рис. 2 на новой плоскости проекций. Для этого в новой системе H,Sиз проекции точки (a)на сохраняющейся плоскости проекций проводят линию связи, перпендикулярную к новой оси проек­ций H/S. На этой линии связи отмечают расстояние от оси H/S до проекции a_sточки на новой плоскости проекций S, равное расстоянию от преобразуемой проекции точки a' до оси проек­ций V/H в системе V,H(| a_s –2|= | a' –1 |). Перемену плоскостей проекций можно производить последователь­но несколько раз.

Четыре основные задачи пре­образования.

1.Определение вели­чины отрезка AB общего положенияпоказано на рисунке 3.

2.Приведение отрезка прямой общего положения в проеци­рующее положение.

Для преобразования проекций отрезка общего положения на чертеже в проецирующее положение требуется введение двух новых плоскостей проекций последовательно: первой – парал­лельно отрезку, второй – перпендикулярно ему с условием перпендикулярности между исходными и новыми плоскостями проекций.

3.Приведение плоской фигуры общего положения в проецирующее положение. Решение основывается на предыдущей задаче. По­строение выполняют с помощью одной из линий частного поло­жения, например горизонтали с проекциями a'f', af, (рис. 1). Новая плоскость проекций S в этом случае выбрана перпенди­кулярно горизонтали AF(ось H/S перпендикулярна проекции af) и соответственно перпендикулярно плоскости H.

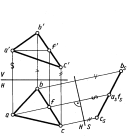
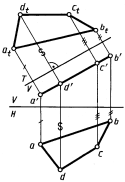
4. Определение натурального вида плоской фигуры, расположенной в проецирующем положении(рис. 2). Построение выполнено путем введения новой плоскости проекций T,перпендикуляр­ной плоскости Vи параллельной плоскости четырехугольника с проекциями a'b'c'd' и a, b, с, d(ось T/V параллельна проекцииa'b'c'd').Проекция a_tb_tc_td_tявляется натуральным видом задан­ного четырехугольника.

Следовательно, последовательным введением двух новых плоскостей проекций могут быть определены: натуральный вид плоской фигуры, принадлежащей плоскости общего положе­ния, и углы наклона плоскости к плоскостям проекций.