16. Распределение скорости по сечению (ламинарный режим).

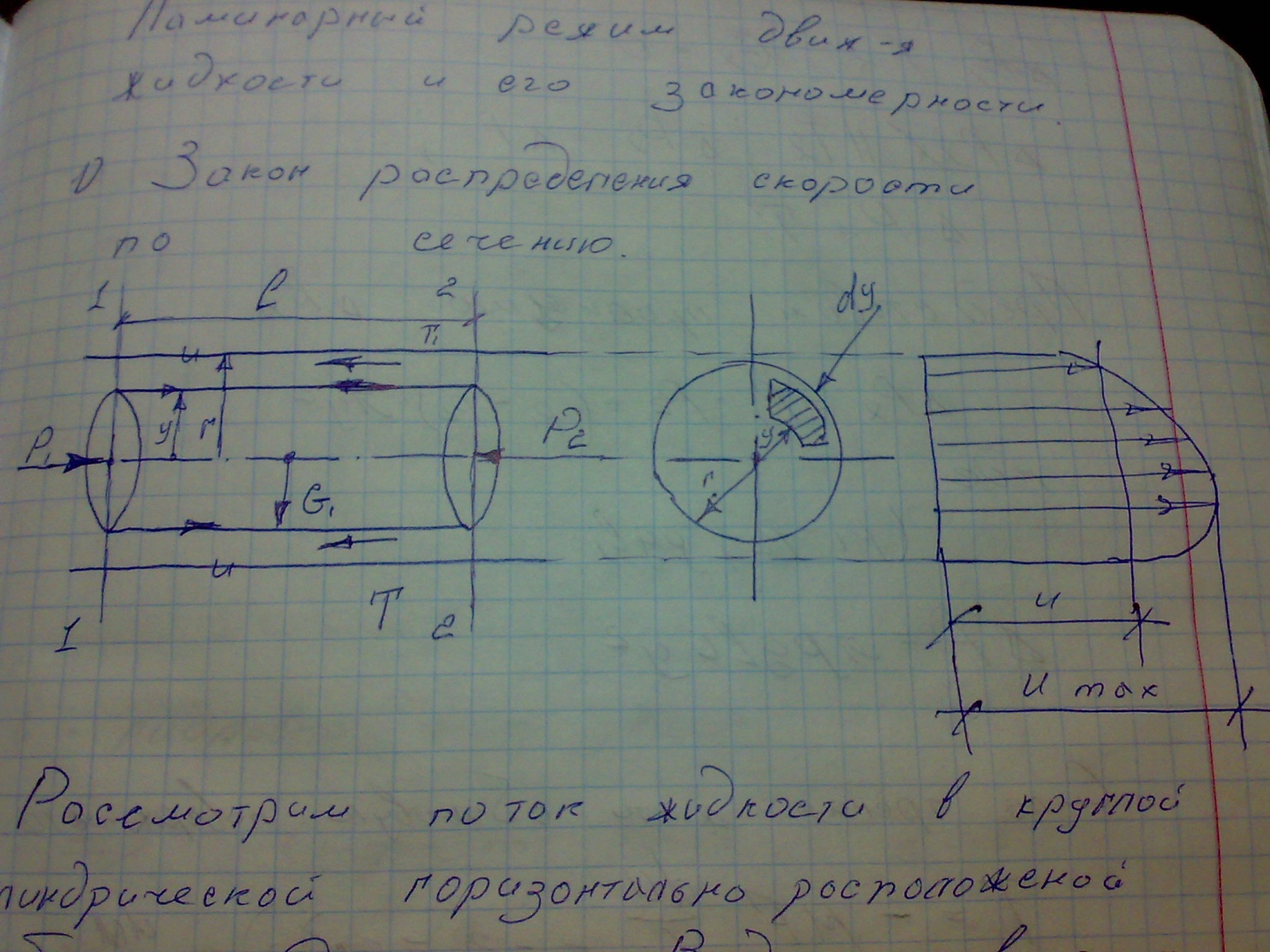
Рассмотрим поток жидкости в цилиндрической горизонтальной трубе радиусом r. Выделим в этой оси элементарный объем жидкости в виде цилиндра радиусом y длинной l. И имеем:

U- скорость движения и направление движения жидкости

p₁,p₂ – силы гидродинамического давления ; T- сила трения ; G- сила тяжести

Спроектируем все силы действующие на оббьем на ось Х для установившегося режима движения жидкости, сумма проекций этих сил должно =0. Т.е

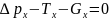
Так как а , то

Расписав проекцию мы получим:

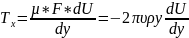
µ- динамическая вязкость ; F- внутренняя площадь поверхности трубы ; υ- кинематическая вязкость жидкости

знак минус для силы трения в этом выражении принимают потому, что с увеличение расстояния от оси потока к стенкам сосуда скорость частиц уменьшается и у стенок сосуда эта скорость будет направлена на встречу потоку. И из этого следует:

И тогда

Где

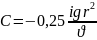
Подставляем

Из этого следует что скорость достигает максимального значения при диаметре струйки равном 0 ;

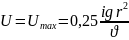
Так как выражение имеет квадратичный вид параболы, то эпюра скорости при ламинарном режиме движения жидкости , у которой всегда будет больше средней скорости.

17. Расход жидкости и средняя скорость потока. Коэффициент кориолиса.

Зная закон распределения скорости по сечению потока определим расход жидкости среднюю скорость и коэффициент Кориолиса. Для этого выделим в поперечном сечении потока элементарное сечение кольцевой формы радиусом у и толщенной dy.

Элементарный расход жидкости через это сечение: dQ=Ud

Представим U:

Поставим в исходное полодение и проинтегрируем

Q = )ydy

После интегрирования получим;

Представим гидравлический уклон i как;

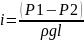
Подставим и получим еще одно выражение для определения расхода жидкости, Закон Пуазейля:

Средняя скорость потока:

Отношение скоростей:

Коэффициент Кориолиса: ,

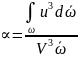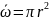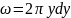Где , d ,то α=2

ЗАКОН ГИДРАВЛИЧЕСКОГО СОПРОТИВЛЕНИЯ КОЭФФИЦИЕНТ ДАРСИ.

Заменив в выражении для средней скорости потока

; Где

Отсюда получим закон гидравлического сопротивления:

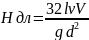
Умножим числитель и знаменатель на 2V получим: H =

Сравнив полученное выражение с выражением для определенияя потерь: Н_пот=

И решая его относительно λ получаем коэффициент Дарси для круглой трубы:

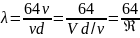
Коэффициент Дарси в общем случае:

Где А = 64……..150

18. Ламинарное течение жидкости в плоских узких щелях.

ОБЛИТЕРАЦИЯ ЩЕЛЕЙ.

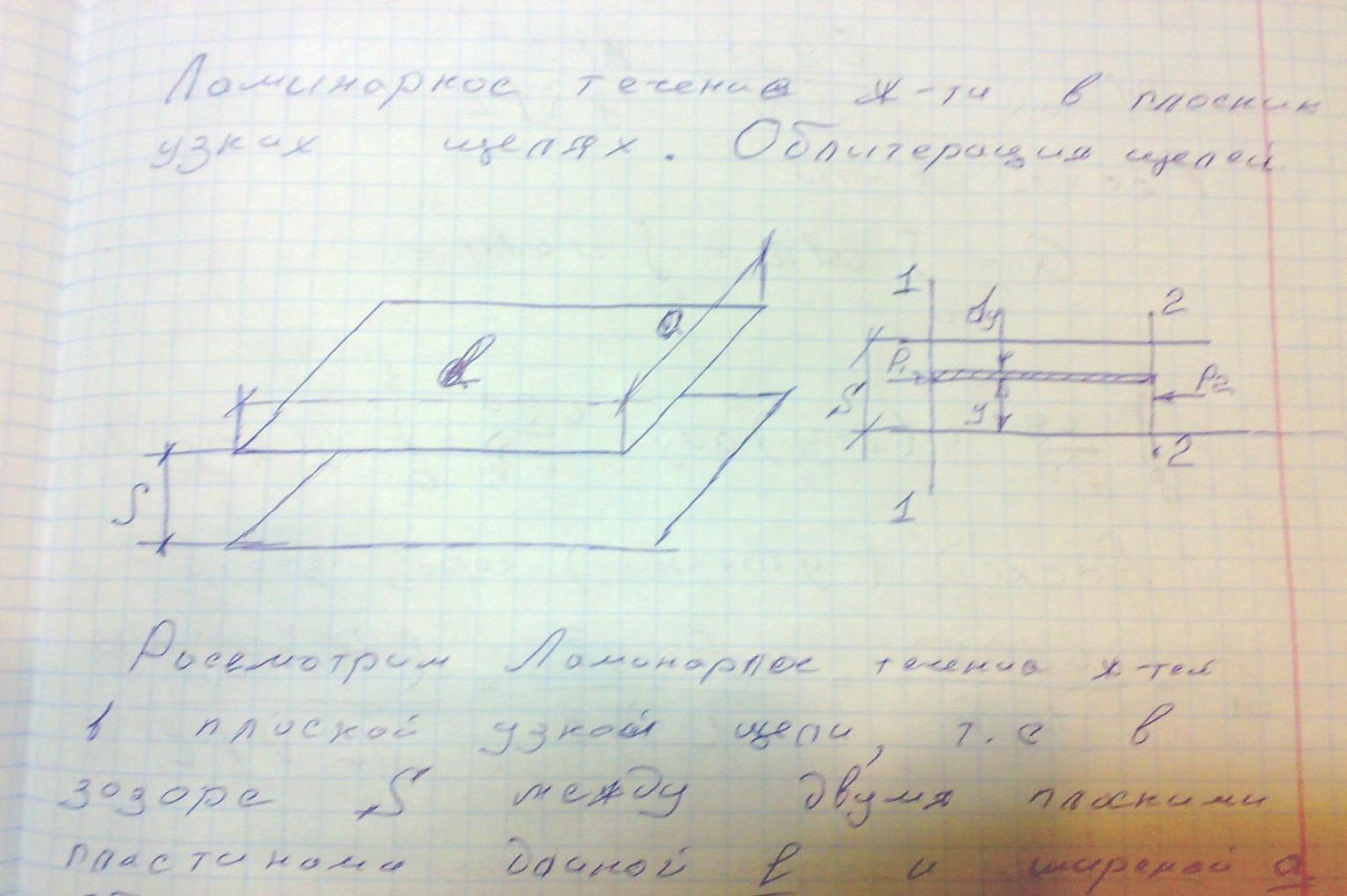
Рассмотрим установившееся равномерное ламинарное течение жидкости в плоской щели — зазоре между двумя неподвижными параллельными пластинами, расстояние между которыми S, причем s< < a s<<L. Обозначим разность давлений на входе и выходе (P₁-P₂) = ∆P

Проведем в потоке в ще ли два сечения I—I и II—II на расстоянии L друг от друга и выделим между этими сечениями симметрично осям Ох и Oz объем жидкости в форме цилиндрической трубки получим уравнение скорости для любой частицы находящиеся в зазоре по вертикале.

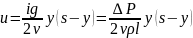
При y=0, т. е. в центре потока, скорость максимальна:

u_max = igs2/(8v)

Расход жидкости

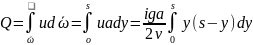
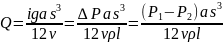
Средняя скорость потока:

Потери напор :

Гидравлический радиус:

Когда жидкость проникает через узкую щель, образованную неподвижными стенками, на границе раздела твердой и жидкой фаз происходит адсорбция поляризованных молекул жидкости, обусловленная силами межмолекулярного взаимодействия. В результате этого на поверхности стенок образуется фиксированный слой жидкости, обладающий определенной прочностью на сдвиг, а живое сечение потока в щели уменьшается. Такое заращивание щели называется облитерацией.

Наращивание облитерационного слоя происходит не бесконечно: чем дальше этот слой от твердой поверхности, тем рыхлее он становится, так как связь молекул ослабляется, и частицы жидкости, отрываясь от поверхности слоя, вытесняются из щели. Интенсивность облитерации зависит от рода жидкости, перепада давления в щели, а также от гидравлического радиуса щели.