14. У равнение гидравлического количества движения (уравнение импульсов).

Известно, что проекция приращения количества движения перемещающегося тела на произвольно намеченную ось равна сумме проекций импульсов внешних сил на эту же ось, действующих на тело за соответствующий промежуток вре­мени. Если внешние силы постоянны во времени, то

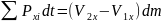
Мысленно выделим в потоке отсек жидкости ABDC (рис. 4.6,а), который, перемещаясь под действием внешних сил, за время dt займет положение A'B'D'C'. На- выделенный отсек жидкости действуют силы: внутренние, попарно равные, дейст­вующие противоположно, и следовательно, уравновешенные; внешние — сила тяжести, поверхностные силы гидродинамиче­ского давления, действующие на торцовые поверхности (плос­кости I—I и II—II), силы трения и реакции стенок.

Масса жидкости входящая в выделенный отсек и выходящие из него, находиться соответственно в объемах и может быть определен через массовый расход. 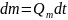тогда

;

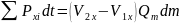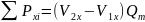– это выражение представляет собой уравнение импульсов.

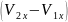При переходе от од­ной выделенной в потоке контрольной поверхности I-I к дру­гой поверхности II—II сумма проекций импульсов наших сил , действующих на отсек потока ABDC (см. рис. 4.6,а) между контрольными поверхностями на любое выбранное направление, равна произве­дению массового расхода потока(Q_m) на приращение проекций на ту же ось средних скоростей жидкости , движущейся через конт­рольные поверхности.

Рассмотрим струю жидкости, выходящую из цилиндрическо­го насадка, расположенного нормально к преграде (рис. 4.6,6). Мысленно выделим отсек потока, ограниченный сечениями I—I и II—II, в которых скорости равны соответственно V₁ и V₂. На отсек действуют: внешние силы , зависящие от давления (P1 и P2— давления в сечениях соответственно I—Iи II—II). Так как P1=Pa и P2=Pа, избыточное давление в этих сечениях отсутствует, сила тяжести G, приложенная в центре тяжести отсека; сила реакции, равная силе давления струи на преграду с об­ратным знаком, Rx = -Рx где Rx – реакция преграды

Проектируя внешние силы и количество движения на ось х, получим: Gx 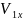= 0; = 0; 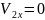; можно записать –Px=ρQ(0-V₁) или Px=ρQV₁

Если расход струи выразить через скорость V₁ и живое сече­ние 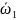то получаем

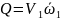
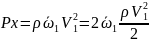
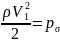– гидравлическое давление потока

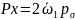
15. Общие сведения о потерях напора по длине и в местных сопротивлениях.

При движении потока реальной жидкости происходят потери напора, так как часть его затрачивается на преодоление гидравлических сопротивлений.

Общие потери напора в потоке:

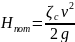
зависят от скоростного напора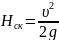 и коэффициента сопротивления системы определяющего число скоростей напоров, которым соответствуют потери напора.

Обычно гидравлические сопротивления подразделяются следующим образом:

Сопротивления по длине, возникающие при движении жидкости по всей длине равномерного потока и зависящие от его длины;

местные сопротивления, возникающие при неравномерном движении жидкости в отдельных местах потока (на различных фасонных участках трубопровода или русла в коленах, тройниках, задвижках, при внезапных сужениях или расширения потока и т. д.) и не зависящие от его длины.

По аналогии с 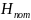потери напора по длине равномерного потока:

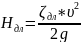
Где 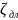- коэффициент сопротивления по длине равномерного потока.

Потери напора в зонах местных сопротивлений могут быть найдены по формуле Вейсбаха: ; Где 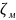- коэффициент местного сопротивления,

Преобразуем формулу и получаем коэффициент Дарси - Вейсбаха для определения потерь напора по длине в круглой цилиндрической трубе:

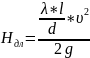
Где 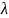- коэффициент Дарси или коэффициент гидравлического трения; 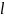длина трубы; v — средняя скорость потока; d - внутренний диаметр трубы; 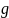-ускорение свободного падения.

В гидравлике для определения сопротивления также используют формулу Шези:

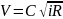; Где

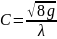
Формула Шези широко используется для расчетов безнапор­ных потоков, гидравлический уклон которых равен уклону дна русла.

Для определения коэффициентов λ и С существует целый ряд формул, некоторые из которых приводятся ниже при рассмотрении закономерностей ламинарного и турбулентного режимов движения жидкости.

Общие потери напора в трубопроводе или в открытом русле определяют арифметическим суммированием потерь напора на прямолинейных участках и в местных сопротивлениях. Этот метод называется принципом наложения (сложения) потерь.

РЕЖИМ ДВИЖЕНИЯ ЖИДКОСТИ. ЧИСЛО РЕЙНОЛЬДСА.

Режимы движения жидкости

Движение потока жидкости находятся в одном из двух режимов:

1) Прямолинейное упорядоченное движение частиц жидкости когда в потоке присутствует только один вектор скорости движения частиц вдоль оси потока – этот режим называется ламинарным

2) Хаотичное движение жидкости при котором в котором элементарные струйки перемешаны. – турбулентный режим

Число Рейнольдса

Рейнольдс установил критерий позволяющий установить режим движения жидкости.

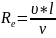
Где - кинематическая вязкость жидкости

Число Рейнольдса соответствующее переходу ламинарного режима в турбулентный находится в интервале

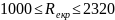
При 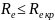– режим движения ламинарный

Пр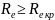и – режим движения турбулентный