- •Основные физические свойства жидкости.
- •Силы, действующие в жидкости. Давление в точке покоящейся жидкости.
- •Диф. Уравнение равновесия жидкости.
- •Осн. Уравнение гидростатики.
- •Сила давления жидкости на плоскую стенку. Центр давления.
- •Сила давления жидкости на криволинейную стенку. Тело давления.
- •Способы описания движения жидкости.
- •Виды движения жидкости и его элементы.
- •Поток. Гидравлические элементы потока.
- •Уравнение неразрывности (сплошности) потока.
- •Диф. Уравнение движения и баланса энергии для невязкой жидкости.
- •У равнение бернулли для элементарной струи невязкой жидкости.
- •Уравнение бернулли для элементарной струи и потока вязкой жидкости.
- •У равнение гидравлического количества движения (уравнение импульсов).
- •Общие сведения о потерях напора по длине и в местных сопротивлениях.
- •Распределение скорости по сечению (ламинарный режим).
- •Расход жидкости и средняя скорость потока. Коэффициент кориолиса.
- •Ламинарное течение жидкости в плоских узких щелях.
- •19. Касательные напряжения при турбулентном режиме движения жидкости. Турбулентный режим движения и его закономерности.
- •Сложные трубопроводы.
- •Гидравлический удар в трубопроводах.
- •Прямой и не прямой удар
У равнение бернулли для элементарной струи невязкой жидкости.
Рассмотрим
установившееся движение элементарной
струйки идеальной жидкости в декартовой
системе координат, в которой плоскость
хОу (рис. 4.2) горизонтальна, а из всех
массовых сил действуют, допустим, только
силы тяжести, проекции которых на
оси координат: Х=0, Y=0, Z = -g . Плоскость хОу
называется плоскостью
сравнения
потенциальной энергии (gdz). С учетом всех
этих условий уравнения примут вид:
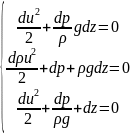
Интегрирование уравнений произведем для двух струйных моделей жидкости — с постоянной плотностью и с переменной плотностью. Для первой модели после интегрирования получим уравнения:
полной удельной энергии
еп=u2/2+p/ρ+ gz = const;
полного давления
Рп =ρu2+p+ρgz = const;
полного напора
Нп=u2/2g+p/ρg+z=const
Эти выражения называются уравнениями Бернулли. Они являются основными при решении многих задач гидравлики и представляют собой математическую модель закона сохранения энергии вдоль элементарной струйки невязкой, несжимаемой жидкости относительно принятой плоскости сравнения
При постоянной плотности
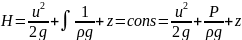 ;
;
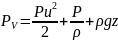
в
этом уравнение
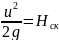 - скоростной
напор
;
- скоростной
напор
;
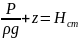 – статический
напор
– статический
напор

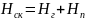 где
где
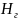 - расстояние от центра тяжести живого
потока жидкости обозначается (z).
- расстояние от центра тяжести живого
потока жидкости обозначается (z).
Этот напор определяет положение потока в пространстве.
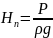 -
пьезометрический
напор,
измеряется пьезометром.
-
пьезометрический
напор,
измеряется пьезометром.
Скорость потока

Скоростной поток
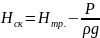
Уравнение бернулли для элементарной струи и потока вязкой жидкости.
П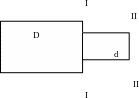 олный
напор в любом сечении струйки вязкой
жидкости определяется теми же
составляющими, что и для невязкой
жидкости. Однако, значения полного
напора в сечениях будут разными, так
как часть энергии расходуется на
преодоление гидравлических
сопротивлений (трение частиц жидкости
друг о друга или о стенки). При этом часть
вода гидравлической энергии преобразуется
в тепловую или механическую и рассеивается
во внешнюю среду. Следовательно, напор
в сечении II—II меньше, чем в сечении I—I
на величину потерь напора, определяемых
разностью полных напоров в соответствующих
сечениях, ∆Н
1-2 =
Н1-1
-
Н2-2Тогда
при р = const уравнения Бернулли для струйки
жидкости будут иметь вид:
олный
напор в любом сечении струйки вязкой
жидкости определяется теми же
составляющими, что и для невязкой
жидкости. Однако, значения полного
напора в сечениях будут разными, так
как часть энергии расходуется на
преодоление гидравлических
сопротивлений (трение частиц жидкости
друг о друга или о стенки). При этом часть
вода гидравлической энергии преобразуется
в тепловую или механическую и рассеивается
во внешнюю среду. Следовательно, напор
в сечении II—II меньше, чем в сечении I—I
на величину потерь напора, определяемых
разностью полных напоров в соответствующих
сечениях, ∆Н
1-2 =
Н1-1
-
Н2-2Тогда
при р = const уравнения Бернулли для струйки
жидкости будут иметь вид:
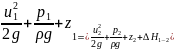 (1)
(1)
Вторая
часть учитывает потери Р:
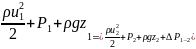
Левые члены уравнений выражают соответственно полный напор, полное давление и полный запас удельной энергии элементарной струйки вязкой жидкости в сечении I—I относительно принятой плоскости сравнения.
Поправочный коэффициент к скоростному напору, определяемому по средней скорости
В отличие от элементарной струйки скорости частиц реальной жидкости в различных точках живого сечения потока неодинаковы, поэтому при определении кинетической энергии жидкости Через ее среднюю скорость допускается неточность, которую необходимо учесть.
Кинетическая
энергий жидкости в сечении элементарной
струйки
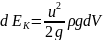 где dV — элементарный объем жидкости,
проходящей через живое сечение
струйки за время t, т. е. dV=tud
где dV — элементарный объем жидкости,
проходящей через живое сечение
струйки за время t, т. е. dV=tud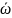 .
.
Следовательно
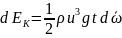 .
Для
потока запас кинетической энергии
.
Для
потока запас кинетической энергии
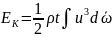 а Скоростной
напор
а Скоростной
напор
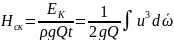
Отношение
действительного скоростного напора к
подсчитанному по средней скорости
называется коэффициентом Кориолиса:
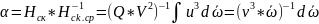
Для
равномерного турбулентного потока
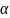 =1÷1,13, для равномерного ламинарного
потока
=1÷1,13, для равномерного ламинарного
потока
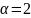 .
Если в уравнения (1) подставить
среднюю скорость v, и поправку к
скоростному напору
,
то получим уравнения Бернулли для потока
вязкой жидкости:
.
Если в уравнения (1) подставить
среднюю скорость v, и поправку к
скоростному напору
,
то получим уравнения Бернулли для потока
вязкой жидкости:
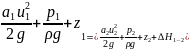
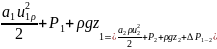 сума
слагаемых уравнения Бернулли представляет
собой суму слагаемых напоров: (скоростного,
пьезометрического, геометрического
напора).
сума
слагаемых уравнения Бернулли представляет
собой суму слагаемых напоров: (скоростного,
пьезометрического, геометрического
напора).
Для
капельной жидкости отношение потерь
напора по длине к самой длине потока
называется гидравлический уклон (i)
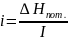 А в частном случаи для горизонтального
потока у которого V1=V2
так как движение упорядочено
А в частном случаи для горизонтального
потока у которого V1=V2
так как движение упорядочено
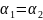 ; Z1
=
Z2
.
; Z1
=
Z2
.
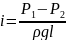 -
гидравлический уклон это характеристика
потока жидкости прямо пропорционально
потерям по длине и обратно пропорционально
длине потока и выражает величину потерь
потока в зависимости от длины потока.
-
гидравлический уклон это характеристика
потока жидкости прямо пропорционально
потерям по длине и обратно пропорционально
длине потока и выражает величину потерь
потока в зависимости от длины потока.
Потери потока
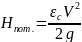
Мощность потока