10. Уравнение неразрывности (сплошности) потока.

У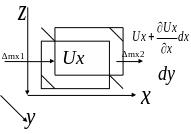 равнение неразрывности или сплошной жидкости основано на законе сохранения массы и исходит из положения механики сплошных сред о том, что в нутрии движущейся жидкости не может произойти разрыв, т. е. установится пустота.

Уравнение неразрывности может быть представлено в дифференциальной форме для

частицы жидкости и элементарной струйки, а также в конечных величинах для потока жидкости. Выделим в потоке элементарный объем. Рассмотрим изменение протекающей массы жидкости по оси Ox. Скорость жидкости вытекающей через левую грань Ux, тогда скорость вытекающей через правую 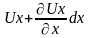, Принимая ρ=const, можно записать, что через левую грань за время dt пройдет масса ∆m_x1 = ;

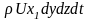А через правую ∆m_x2 = где (dxdydz = dV)

Разность этих масс составит ∆m_x =

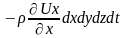
Рассматривая по аналогии изменение массы жидкости по осям Oy и Oz, запишем

∆m_y =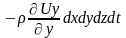 и ∆m_z =

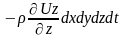
Закон сохранения массы требует, чтобы общее изменение массы, прошедшей через выбранный объем, равнялось нулю

=0

Или (1)

Уравнение (1) называется уравнением неразрывности или сплошности в дифференциальной форме для произвольного движения не6сжимаемой жидкости. При установившемся движении уравнение неразрывности можно вывести исходя из свойств элементарной струйки, в соответствии с которым жидкость из струйки не вытекает в стороны и не притекает в нее извне, но в то же время местные скорости разные по длине струйки. Отсюда следует, что количество жидкости, притекающей к струйке в начальном сечении и вытекающей из нее в конечном сечении, равны между собой и общий объем жидкости в струйке не изменяется т. е. 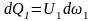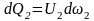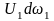элементарные расходы в единицу времени: втекает , вытекает и тогда 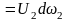(2) Выражение (2) и является уравнением неразрывности для элементарной струйки.

Для потока жидкости уравнение неразрывности будет иметь вид: 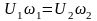или 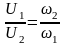Т. е. отношение средних скоростей в сечениях потока обратно пропорционально отношению их площадей. Из этого следует, что при установившемся сечении с уменьшением площади сечения средняя скорость увеличивается и наоборот.

11. Диф. Уравнение движения и баланса энергии для невязкой жидкости.

При движении невязкой (идеальной) жидкости а так как идеальная жидкость — это жидкость, лишенная вяз­кости, в ней при движении не возникают силы внутреннего тре­ния и, как следствие, отсутствует рассеивание энергии. Таким образом, запас энергии в элементарной струйке по длине пото­ка жидкости постоянен.

В движущейся жидкости кроме объемных и поверхностных сил действуют силы инерции. Пользуясь принципом Даламбера, составим уравнение движения единицы массы жидкости, ко­торое представляет собой сумму проекций массовых и поверх­ностных сил:

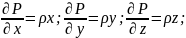
Если к ним прибавить с обратным знаком проекции сил инерции, отнесенных к единице массы То:

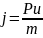
Получим: ; ; ;

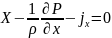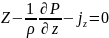Подставив в эти уравнения величины 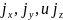и учитывая что при установившемся движения: , получим уравнение движения Эйлера:

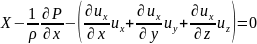
Мерой движения жидкости является энергия, которая харак­теризуется работой, совершаемой жидкостью при торможении (кинетическая энергия), и работой, совершаемой массовыми и поверхностными силами (потенциальная энергия) при переходе от рассматриваемого положения в пространстве к нулевому по­ложению, в котором потенциальная энергия условно считается равной нулю. Следовательно, для получения уравнения энергии необходимо найти работу сил при перемещении единицы массы жидкости на расстояние dl по линии тока, для этого умножим почленно каждое из выражений на массу m и проекцию dl на каждую координатную ось. Выполнив все необходимые преобразования получим выражение для полной энергии:

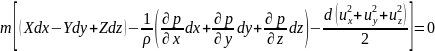
И окончательно будем иметь

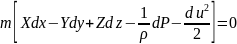
Уравнение баланса движения потока невязкой жидкости в общем виде.

Из полученного уравнения вытекает три частных случая:

1. Уравнение баланса энергии потока невязкой жидкости не зависимо от массы :

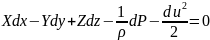
2. Уравнение баланса энергии не зависящие от объёма:

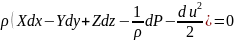
3. Баланс энергии отнесенный к силе тяжести:

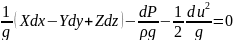
В гидравлике это уравнение еще называют напором.