2. Силы, действующие в жидкости. Давление в точке покоящейся жидкости.

Жидкость в состоянии покоя или движения находится под дей­ствием различных сил, которые в соответствии с их природой можно разделить на две группы:

• Поверхностные.

• Массовые.

Поверхностные силы приложены к поверхности, ограничи­вающей рассматриваемый объем жидкости или намеченной внутри этого объема. При равномерном распределении этих сил по данной поверхности их числовое значение пропорционально числовому значению ее площади. К поверхностным силам отно­сятся силы, действующие на поверхность жидкости по перпенди­кулярным направлениям (силы давления), по касательной (силы поверхностного натяжения), а также силы внутреннего трения (последние имеют место только при движении жид­кости).

Массовые силы действуют на все частицы рассматриваемого объема жидкости. При равномерном распределении этих сил по данному объему их числовое значение пропорционально число­вому значению ее массы (объема). К массовым силам относят­ся силы тяжести и силы инерции.

В гидравлике жидкость рассматривается как непре­рывная сплошная среда, в которой отсутствуют силы, дейст­вующие в точке. Поэтому в отличие от динамики твердых тел в гидравлике обычно рассматривают не сами силы, а плотность их распределения в сплошной среде: либо предел отношения элементарной поверхностной силы к элементарной площади, либо предел отношения элементарной массовой силы к, элемен­тарной массе рассматриваемого объема жидкости, т. е. единич­ные силы.

Единичные поверхностные силы представляют собой напря­жжения:

• Касательные

• Нормальные (при сжатии жидко­сти напряжение сжатия называется давлением Р), а единичные массовые силы — ускорения j .

Проекции результирующей еди­ничных массовых сил или результирующего ускорения на коор­динатные оси обозначают jx = X, jy = Y, jz = Z.

ДАВЛЕНИЕ В ТОЧКЕ ПОКОЮЩЕГОСЯ ЖИДКОСТИ

В ыделим вокруг точки А находящейся внутри покоящейся жидкости произвольный объем _∆V , рассечем этот объем произвольной плоскостью на 2 части одну из которых мы мысленно отбросим (например первую) а вторую рассмотрим в состоянии равновесия заменив действие отброшенной части на нее силами:

• Нормальной силой _∆Р

• Касательной силой _∆Т

• Равнодействующей _∆R

Средняя величина давления жидкости на выделенную площадку _∆F равна:

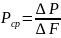
Элементарная сила давления действующая на эту бесконечно малую площадку будет равна:

Давление в точке покоящейся жидкости обладает 2 свойствами:

– Сила давления в точке всегда нормально к поверхности воспринимающей это давление.

– Сила давления в точке во всех направлениях одинакова по своему значению.

3. Диф. Уравнение равновесия жидкости.

В ыделим вокруг точки А находящейся внутри покоящейся жидкости элементарный объем в виде параллелепипеда с ребрами dx ; dy ; dz : тога при величине давления в точке А = P давление на левую и правую грани будут иметь следующие значения :

- на правую грань

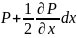
- на левую

А элементарные силы давления на эти грани:

;

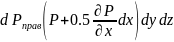
Кроме этих сил на выделенный объем действуют еще и массовые силы результирующие которых равны:

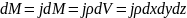
Спроектируем эти силы на ось ОХ и прировняем их сумму к нулю:

-

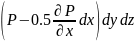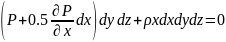
После преобразований получим: 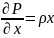, спроектировав остальные силы на оси Оx и Oz и сделав аналогичные преобразования получим систему уравнений:

Эти уравнения представляют собой общие условия равновесия жидкости в дифференциальной форме и называются они уравнениями Эйлера.

Для приведения уравнения Эйлера к удобному для интегрирования виду каждое из уравнений умножим на dx ; dy ; dz почленно сложим и получим:

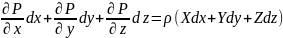
Левая часть этого выражения называется полным дифференциалом гидростатического давления и обозначается dP

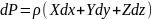
Это уравнение устанавливает функциональную зависимость давления жидкости от координат жидкости и позволяет определить Р в любой точке покоящейся жидкости.