Энтропия непрерывного множества

На практике мы сталкиваемся с ситуацией, когда число исходов опыта может

быть сколь угодно велико, т.е. k  ∞ . При этом вероятность каждого исхода стремится к нулю (p0), а искомый корень может принимать все возможные значения в заданном интервале (k ). Из теории вероятности известно, что в данном случае необходимо использовать плотность распределения вероятности Р(х).

Эта функция обладает тем свойством, что величина Р(х)dх есть вероятность того, что переменная x (значения корня в рассматриваемом примере) примет значения, заключенные в интервале от х до (х + dх).

Для оценки неопределенности опыта необходимо использовать энтропию непрерывного множества, которое по аналогии с энтропией дискретного множества (6) имеет вид:

(12)

При этом всегда

(аналогично случаю дискретного множества Σp_i=1 ). Интегрирование осуществляется в интервале переменной х. Энтропия непрерывного множества (12) обладает большинством свойств энтропии дискретного множества.

Распределение Р(х), которое соответствует максимальному значению энтропии, имеет вид:

где x₀, x₁ - пределы интегрирования.

При этом, если обозначить l=x₁-x₀, то вероятность обнаружить корень уравнения на отрезке длиной l внутри интервала dх равна p=dx/l

По определению вероятности:

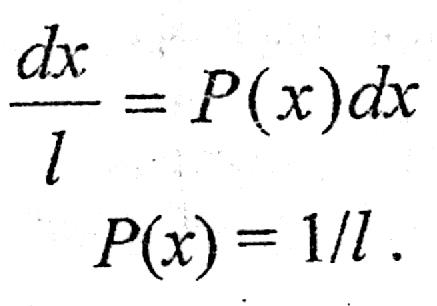(13)

Перепишем формулу (12) с учетом (13)

Итак, энтропия непрерывного множества запишется

(14)

Это выражение аналогично для энтропии дискретного множества (4).

Таким образом, если для дискретного множества энтропия измеряет неопределенность (неупорядоченность) абсолютным образом и энтропия дискретного множества всегда положительна, то в случае непрерывного множества под логарифмом формулы (14) может стоять величина меньше единицы и энтропия примет отрицательное значение.

Количество информации как критерий оценки степени организованности системы.

Как показано выше, энтропия является не только мерой неопределенности (7), но и мерой разнообразия, неупорядоченности, хаоса (9). Тогда вместо определения «устраненная неопределенность» можно употребить термин «блокированное разнообразие».

Термин «устраненная неопределенность» относится к энтропии, записанной через вероятность (7). Это определение ближе к теории информации (см. п. «Энтропия как мера количества информации»):

Если энтропия является мерой разнообразия (9), то употребляется термин «блокированное разнообразие». Это определение ближе к физике, термодинамике:

(15)

где I - блокированное разнообразие;

Н_вх - энтропия, оценивающая неупорядоченность на входе системы; Н_вых - энтропия, оценивающая неупорядоченность на выходе системы.

В кибернетике биологом Эшби был сформулирован закон «необходимого разнообразия». Согласно закону Эшби: каждая система, блокирующая разнообразие, должна иметь собственное разнообразие не менее блокированного, т.е. «только разнообразие может уменьшить другое разнообразие».

Критерии степени оценки организованности системы в общем виде записывается как отношение

(16)

где η - критерий оценки степени организованности системы.

С помощью критерия η может оцениваться как разделительная способность колонны, так и многоколонной установки в целом.

С точки зрения характера воздействия на организованность системы варьируемые параметры можно разбить на две группы: интенсивные и экстенсивные.

Интенсивные параметры в состоянии повысить организованность системы (качество разделения) при неизменных затратах работоспособной энергии и фиксированных энергетических затратах. Изменение этих параметров обязательно приводит к экстремальному значению критерия, качества разделения.

Экстенсивные параметры могут повысить организованность системы только за счет энергетических или неэнергетических затрат.

Двойственный характер энтропии и количества информации.

Энтропия является количественной мерой неопределенности случайного объекта. Неопределенность статистического типа можно измерить (7)

Количество информации определяется как мера снятой неопределенности (11)

В рассмотренном выше случае энтропия носит функциональный характер и применяется в теории информации.

Энтропия допускает и другое толкование (пример с шарами). В данном случае энтропия выступает как мера разнообразия, неупорядоченности, хаоса (9).

Энтропия как мера разнообразия ближе к физике, термодинамике и используется для оценки степени организованности системы. В данном случае энтропия носит атрибутивный характер.

Двойственный (функциональный и атрибутивный) характер энтропии и

информации.

Характер энтропии и информации	Энтропия	Информация	Область применения
Функциональный	Мера неопределенности	Мера количества информации	Теория информации
Атрибутивный*	Мера разнообразия, неупорядоченности, хаоса	Мера степени организованности системы	Физика и техника

* Атрибутивное - неотъемлемое, существенное свойство материи.