Энтропия и информация в системном анализе.

Современное понимание информации и ее роль в искусственных и естественных системах сложилось не сразу. Информация - это совокупность знаний, полученных разными науками: физикой, биологией, философией, теорией связи и т.д.

С другой стороны к этой проблеме пришла философская теория познания. Признав, что наше знание есть отражение реального мира, материалистическая теория познания установила, что отражение является всеобщим свойством материи. Сознание человека является специфической формой отражения.

Как только состояние одного объекта находится в соответствии с состояниями другого объекта, мы говорим, что один объект отражает другой, содержит информацию о другом.

В настоящее время информация рассматривается как фундаментальное свойство материи. Понятие информации столь же фундаментально для всей системологии как и понятие энергии для физики.

Исследуя информацию, кибернетика не открыла нового свойства материи: оно известно в философии под названием свойства отражения. Новое состоит в том, что информацию можно исследовать количественно.

Энтропия дискретного множества. Понятие неопределенности.

В системном анализе теоретическим ядром являются понятия энтропия и количество информации. Энтропия выступает как мера неопределенности. Характер неопределенности может быть самым различным, например:

- неопределенность типа незнания

- неопределенность типа расплывчатости

- неопределенность статистического типа

Неопределенность статистического типа можно свести к теории вероятности и измерить. Введем количественную меру для данного типа неопределенности.

Сосредоточим внимание по сущности неопределенности и рассмотрим несколько простейших опытов, которые обозначим А, Б и В.

Введем характеристики опыта:

k - число исходов опыта;

p_i - вероятность г-го исхода опыта (i=1,k);

H - мера неопределенности результата опыта.

Опыт А будет заключаться в подбрасывании монеты. В этом опыте возможны два исхода (k=2). Монета упала гербом вверх, либо вниз. Вероятность каждого исхода p_i =1/2 (i=1,2).

Опыт Б - подбрасывание игральной шестигранной кости. В этом опыте возможны шесть исходов (k=6). Вероятность каждою исхода p_i =1/6(i=1,6).

Опыт В предполагает одновременное подбрасывание двух игральных костей. Для этого опыта k=36 и p_i =1/36 (i=1,36).

Оценка неопределенности результатов этих опытов есть оценка трудности угадывания исходов опытов. Из всех описанных опытов опыт В имеет максимальную неопределенность, поскольку число исходов здесь самое большое и заранее предвидеть исход этого опыта труднее всего. Чтобы перейти к количественной оценке неопределенности, сформулируем основные требования к функции, которая должна выполнять роль меры неопределенности Н.

Так как любая теория строится па аксиоматике, постулируем.

1)Значение Н монотонно возрастающая функция при увеличении числа

исходов опыта, Н=f(k).

2) Значение H = 0, если опыт имеет единственный исход, (k=1 ). Это означает,

что никакой неопределенности не возникает и результат опыта очевиден.

3)Неопределенность двух опытов Б следует рассматривать как

неопределенность одного опыта В, т.е. суммарное значение энтропии двух

опытов Б равно энтропии опыта В. Нельзя утверждать, что это два опыта Б

или один опыт В, т.к. ситуация неразличима. Оценка неопределенности

обладает свойством аддитивности. Это положение следует из того, что эти

две ситуации физически неразличимы. По умолчанию мы принимаем, что

вероятность каждого исхода опыта одинакова.

2Н_Б = Н_В

где H=f(k) - неопределенность опыта Б;

H=f(k²) - неопределенность опыта В;

k - число исходов опыта Б.

2f(k) = f(k²)

В общем виде для п простых опытов можно записать:

nf(k) = f(k²) (1)

Функциональное уравнение (1) можно решить относительно функции f(k). Дифференцируем уравнение (1) по k , используя свойство монотонности функции f(k).

(2)

Далее дифференцируем выражение (1 ) по п

(3)

Разделим уравнение (2) на (3)

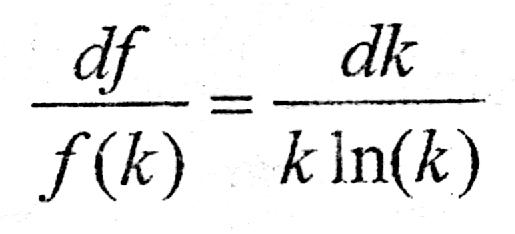
Интегрируя, находим:

где ln(С) - постоянная интегрирования. Из последнего выражения следует

Получено простое решение уравнения (1), но С определить нельзя, так как нет необходимой информации для отыскания постоянной интегрирования.

Так как с увеличением k энтропия растет, то С >0, и последнее выражение можно переписать в окончательном виде:

(4)

Из этого выражения видно, что оно удовлетворяет второму исходному постулату.

Итак, при k равновероятных исходах неопределенность опыта составляет:

(4*)

где p=1/k — вероятность исхода опыта.

Если учесть, что для равновероятных исходов

, то умножая (4*) на единицу в виде , получим

(5)

Каждый член правой части выражения (5) можно рассматривать как вклад отдельного исхода в общую неопределенность опыта. В случае равновероятных исходов вклад каждого исхода одинаков.

Выражение (5) можно записать в компактной форме:

(6)

Если число опытов N то в силу аддитивности энтропии

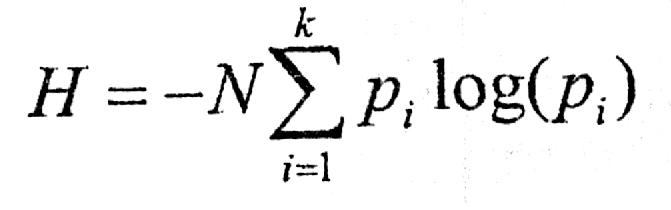(7)

Функция (6) называется средняя энтропия опыта, энтропия выбора, а также информационная энтропия дискретного множества. Энтропия как мера неопределенности (7) была введена Шенноном при разработке математической теории связи.

Основные свойства энтропии.

Рассмотрим основные свойства энтропии дискретного множества. Прежде всего отметим, что энтропия дискретного множества не может принимать отрицательного значения. Так как 0 ≤ р ≤ 1 , то величина -plog(р) всегда положительна.

Если р  0 , то -р1og(р)  0 , если p1, то также - р1оg(p)  0 .

Так как -рlog(р) = 0 только при p=0 или р=1 , то энтропия опыта равна нулю только в том случае, когда одна из вероятностей равна единице, следовательно, все остальные равны нулю. Это хорошо согласуется со смыслом величины H как меры неопределенности: в этом случае опыт не содержит

никакой неопределенности, так как результат опыта можно предвидеть заранее. Рассмотрим пример: в ящике находятся белые и черные шары одного размера. Вынимаем наугад шар из ящика. Данный опыт имеет два исхода: мы можем вынуть из ящика только белый или черный тар.

Запишем формулу энтропии для двух исходов опыта:

где р₁ - вероятность извлечения белого тара;

р₂ — вероятность извлечения черного тара, р₂=1-p₁