7.1 Частотные характеристики замкнутой системы.
Проделывая аналогичные действия найдем частотные характеристики замкнутой системы:
Рисунок 7.7 Вещественная частотная характеристика.
Рисунок 7.8 Мнимая частотная характеристика.
Рисунок 7.9 Амплитудно-фазовая частотная характеристика.
Рисунок 7.10 Амплитудная частотная характеристика.
wc = 0.5 (найдено по следу функции)
Рисунок 7.11 Фазовая частотная характеристика.
Рисунок 7.12 Логарифмическая амплитудная характеристика.
8 Построение для выбранных параметров регулятора временных характеристик замкнутой системы
Все характеристики будут построены для значения параметров k1=40, k3=0.1
Существует две временных характеристики: импульсная и переходная.
Импульсная временная характеристика получается при задании на входе функции Дирака и задается следующей формулой:
.
Знание импульсной характеристики
позволяет вычислить сигнал на выходе
элемента при любом входном сигнале. По
правилу преобразования Лапласа получаем
свертку
,
которая и дает значение выходного
сигнала.
В нашем случае передаточная функция замкнутой системы имеет вид:
Таким образом, импульсная характеристика имеет вид:
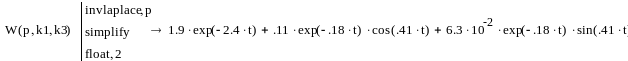
Построим график импульсной характеристики:
Рисунок 8.1 Импульсная характеристика замкнутой системы.
Вторая временная характеристика
называется переходной, когда на вход
подается сигнал
.
Переходная характеристика
может быть найдена по следующей формуле:
,
где
.
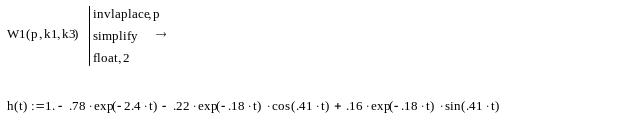
Рисунок 8.2 Переходная характеристика замкнутой системы.
Между импульсной и переходной характеристикой существует связь:
,
или
,
Таким образом, импульсная временная характеристика есть производная по времени от переходной, и наоборот — переходная временная характеристика является интегралом от импульсной.
9 Заключение
В ходе курсового проектирования были выполнены следующие задачи.
1. Исходная структурная схема системы управления была преобразована и получена эквивалентная передаточная функция системы.
2. Была построена область устойчивости на плоскости параметров регулятора, была произведена проверка найденной области устойчивости по критерию Гурвица.
3. Произведено построение годографа Михайлова для сочетания параметров регулятора из области устойчивости, области неустойчивости и на границе устойчивости. Были на практике проверены теоретические сведения о виде годографа для сочетания параметров из этих областей.
4. Осуществлен выбор параметров регулятора по заданным показателям установившегося режима:
5. Для найденных параметров регулятора были построены частотные характеристики разомкнутой и замкнутой системы, временные характеристики замкнутой системы.
10 Список литературных источников
Основы автоматического регулирования и управления. Под ред. В.М. Пономарева и А.П. Литвинова, М.: Высшая школа, 1974.
Теория автоматического управления. Под ред. А.В. Нетушило, М.: Высшая школа, 1976.
Топчеев Ю. И., Цыпляков А. П. Задачник по теории автоматического регулирования.
Воронов А.А., Титов В.К., Новогранов Б.Н. Основы теории автоматического регулирования и управления.
Дьяконов В. Mathcad 8/2000:специальный справочник, Спб:Питер, 2001. – 592 с.