
- •Содержание
- •5.2 Годограф Михайлова для сочетания параметров регулятора из области
- •Введение
- •1 Теоретическая часть.
- •1.1 Типовые структурные схемы системы управления.
- •1.2 Эквивалентное преобразование структурных схем.
- •1.3 Характеристики элементов систем управления.
- •1.4 Устойчивость систем управления.
- •1.5 Оценка качества в переходных процессах систем управления.
- •1.6 Временные характеристики.
- •1.7 Частотные характеристики.
- •2 Исходные данные.
- •3 Получение эквивалентной передаточной функции.
- •4 Построение области устойчивости на плоскости параметров регулятора.
- •5 Построение годографа михайлова для сочетания параметров регулятора.
- •6 Выбор параметров регулятора по заданным показателям установившегося режима и переходного процесса
- •6.1 Характеристики установившегося режима.
- •6.2 Характеристики переходного процесса.
- •7 Построение для выбранных параметров регулятора частотных характеристик
- •7.1 Частотные характеристики разомкнутой системы.
- •7.1 Частотные характеристики замкнутой системы.
- •8 Построение для выбранных параметров регулятора временных характеристик замкнутой системы
- •9 Заключение
- •10 Список литературных источников
4 Построение области устойчивости на плоскости параметров регулятора.
Построим область устойчивости на плоскости параметров k1, k3 выбранного регулятора.
В эквивалентной передаточной функции системы выделим знаменатель, который представляет собой характеристический полином:
![]()
Для удобства дальнейших вычислений подставим значения известных коэффициентов и упростим выражение:
![]()
Найдем соотношение между коэффициентами полинома, используя критерий Гурвица с учетом необходимого и достаточного условия:
Необходимое условие утверждает, что система будет устойчива, если все коэффициенты характеристического полинома положительны:
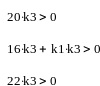
Условие достаточности (произведение средних коэффициентов должно быть больше произведения крайних для системы третьего порядка):
![]()
Объединяя необходимое и достаточное условия, получаем систему неравенств, задающую область устойчивости на плоскости параметров k1, k3:
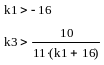
Данной системе неравенств, задающей область устойчивости на плоскости параметров k1, k3, соответствует заштрихованная область на следующем рисунке.
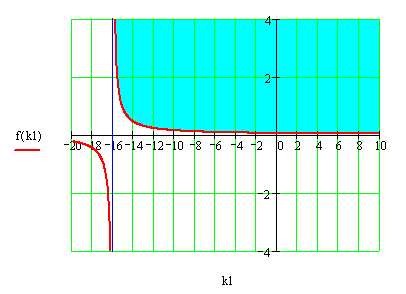
Рисунок 4.1 Область устойчивости на плоскости параметров регулятора.
Сделаем проверку.
1. Возьмем точку из предполагаемой области устойчивости.
k1 = 2, k3 = 2:
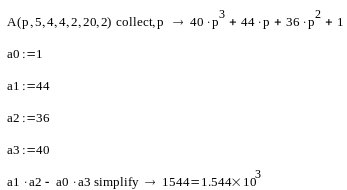
Т.к. все ai>0 и определитель Гурвица положителен – система устойчива.
2. Возьмем точку из предполагаемой области неустойчивости.
k1 = -18, k3 = -2:
![]()
т.к. a1 = -44, то в данной точке система неустойчива.
3. Возьмем точку на предполагаемой границе устойчивости:
k1 = 0, k3 = 5/88.
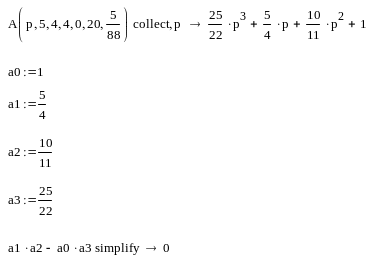
Т.к. определитель Гурвица в данной точке равен 0, то система находится на грани устойчивости.
5 Построение годографа михайлова для сочетания параметров регулятора.
Годограф – это параметрическая кривая,
описанная на плоскости или в пространстве,
либо кривая, описанная концом вектора,
при изменении какого-либо параметра. В
нашем случае – это w. Таким
образом, заменяем
![]() .
.
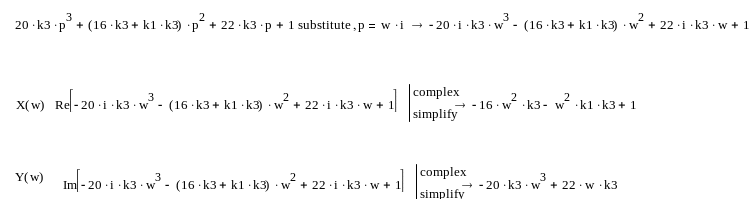
Годограф Михайлова для параметров регулятора из области устойчивости:
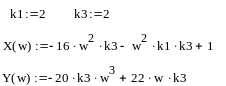

Рисунок 5.1 График зависимости X(w) (область устойчивости).

Рисунок 5.2 График зависимости Y(w) (область устойчивости).

Рисунок 5.3 Годограф Михайлова для области устойчивости.
Годограф для параметров регулятора из области неустойчивости:
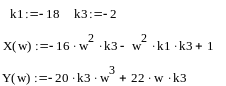
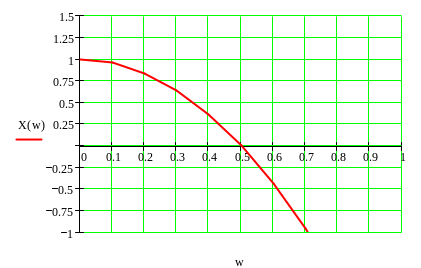 Рисунок
5.4 График зависимости X(w)
(область неустойчивости).
Рисунок
5.4 График зависимости X(w)
(область неустойчивости).

Рисунок 5.5 График зависимости Y(w) (область неустойчивости).

Рисунок 5.6 Годограф Михайлова для области неустойчивости.
Годограф для параметров регулятора на границе устойчивости:

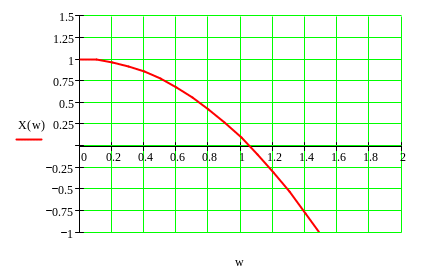
Рисунок 5.7 График зависимости X(w) (область на границе устойчивости).

Рисунок 5.8 График зависимости Y(w) (область на границе устойчивости).

Рисунок 5.9 Годограф Михайлова для области на границе устойчивости.
