1.4 Устойчивость систем управления.
Устойчивость системы управления – это способность системы возвращаться в состояние равновесия (стационарный режим) после прекращения действия причин, вызвавших отклонение от этого состояния.
Пусть сигнал на выходе
или
.
Тогда, если
,
то система будет устойчивой по определению.
Такое условие будет выполняться, если
все вещественные части корней
характеристического уравнения
отрицательны. Таким образом, для линейной
системы управления необходимое и
достаточное условие устойчивости –
это отрицательность вещественных частей
всех корней характеристического
уравнения или, что то же самое, расположение
этих корней на комплексной плоскости
левее мнимой оси.
Критерий Гурвица
Рассмотрим систему с характеристическим
полиномом
-ого
порядка:
Для устойчивости такой системы необходимо:
Положительность всех диагональных миноров определителя Гурвица.
.
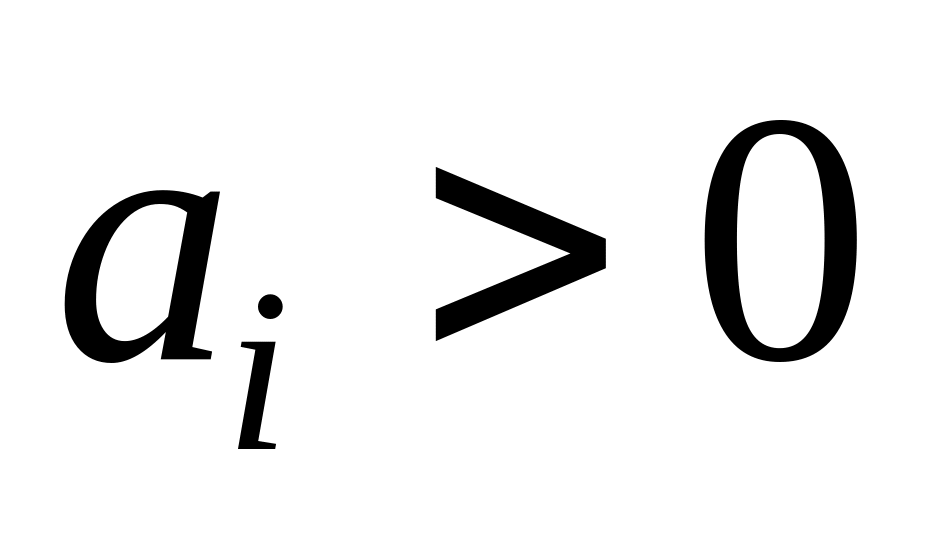Построение определителя Гурвица
Определитель Гурвица представляет
собой матрицу
,
где n – порядок
характеристического полинома.
Алгоритм построения определителя Гурвица следующий:
в 1-й строке определителя Гурвица записываются коэффициенты характеристического полинома с нечетными индексами в порядке возрастания. Оставшиеся свободные места заполняются нулями;
во 2-й строке записываются коэффициенты с четными индексами (и нули). Оставшиеся места заполняются нулями;
3-я строка получается из 1-й строки сдвигом на 1 место вправо, причем образовавшиеся места заполняются нулями;
и так далее, пока не заполнятся все строки.
Критерий Гурвица для систем различного порядка
Система первого порядка:
,
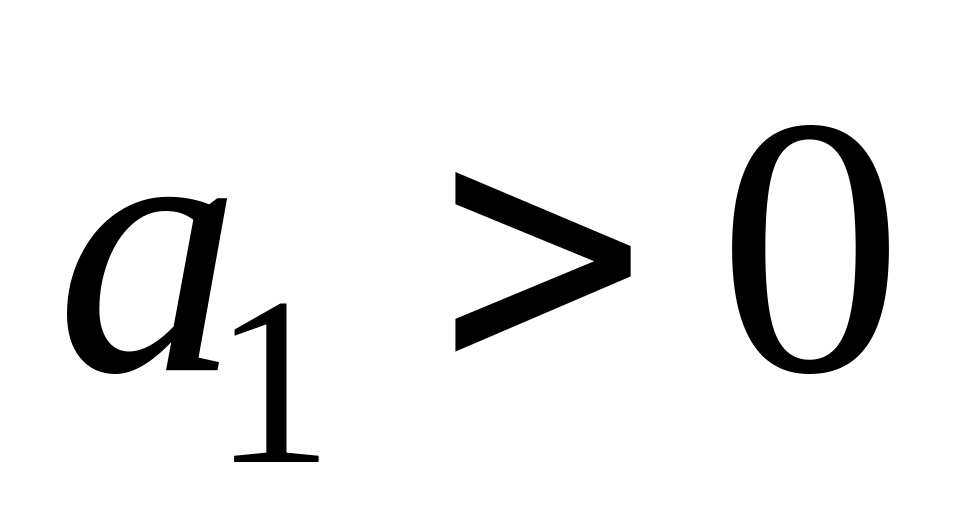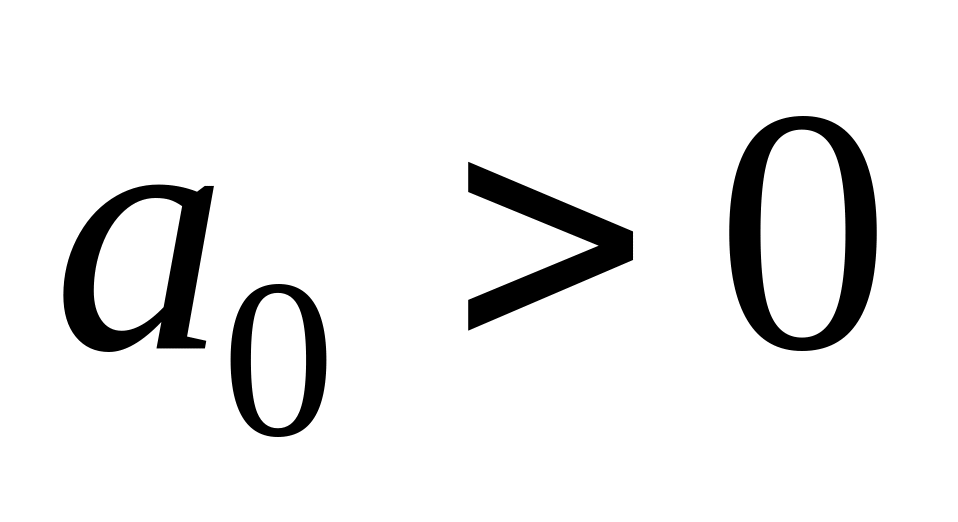— необходимые и достаточные условия
совпадают.Система второго порядка
.Система третьего порядка:
:
:
.
,
,
.
,
,
,
Если
,
то
.
Четвертого порядка:
.
Достаточное условие:
.
Система на границе устойчивости
,
.
Если выполняются условия и один из
определителей Гурвица равен нулю, то
система находится на границе устойчивости,
при этом два корня будут на мнимой оси.
Построение областей устойчивости
Такая задача возникает, если передаточная функция системы между входом и выходом зависит от параметров. В практических задачах привлекаются дополнительные ограничения на параметры, вытекающие из сущности задачи (физический смысл). Если число параметров больше двух, то можно строить сечения.
1.5 Оценка качества в переходных процессах систем управления.
Классификация методов оценки качества:
Прямые оценки.
Корневые оценки.
Частотные оценки.
Интегральные оценки.
Прямые оценки качества
Эти оценки осуществляются непосредственно по переходной характеристике h(t).
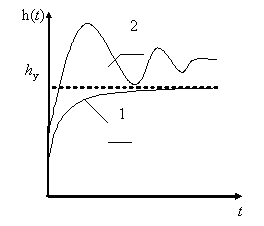
Качественная характеристика разделяет все переходные процессы на монотонные (кривая 1) и колебательные (кривая 2). В качестве количественных оценок используются следующие:
Перерегулирование.
,
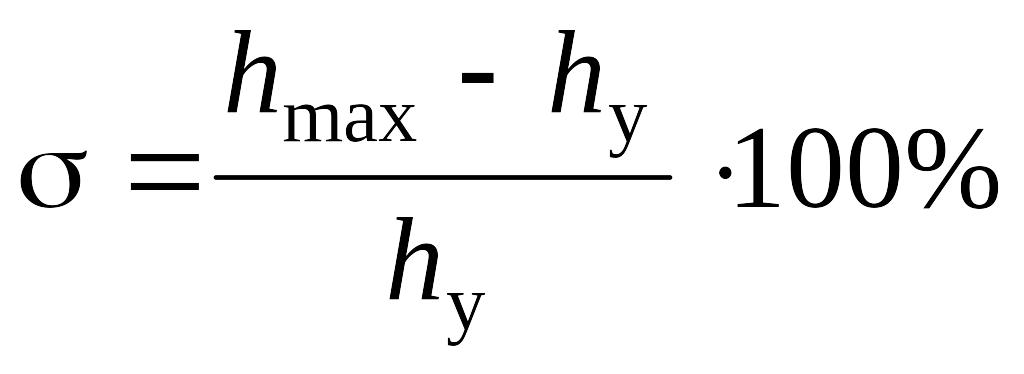где
- максимальное значение переходной
характеристики.
- установившееся значение переходной
характеристики.
Для монотонных процессов перерегулирование
равняется 0, так как
.
Время регулирования (
).
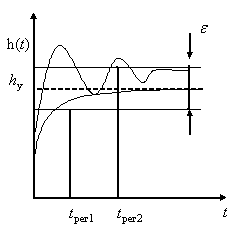
В окрестности выделяется полоса шириной . Время регулирования определяется, как время, за которое кривая переходной характеристики попадает в полосу и остается в ней ( выбирается в % от , =(2%,5%,10%) )