
- •Построение системы автоматического управления
- •Классификация систем автоматического управлении
- •Статистические характеристики элементов системы.
- •Статистические характеристики соединения звеньев.
- •Параллельное соединение звеньев
- •Последовательное соединение звеньев
- •Охват звена жесткой обратной связью
- •5. Виды статических ошибок (вывод формул).
- •6. Астатические элементы и системы.
- •Методы описания динамики линейных систем автоматического управления.
- •8. Классические методы решения дифференциальных уравнений
- •9. Операторные методы решения дифференциальных уравнений
- •10. Матричный метод решения уравнения.
- •11.Устоичивость автоматических систем.
- •12.Определение устойчивости по корням характеристического уравнения.
- •13.Теорема Ляпунова.
- •14. Частотные характеристики.
- •15. Логарифмические частотные характеристики.
- •16. Передаточные функции
- •17. Передаточные функции соединение звеньев.
- •18. Связь передаточных функций и частотных характеристик.
- •19.Типовые динамические звенья и их характеристики.
- •Типовые динамические звенья
- •20.Интегрирующее звено.
- •21.Идеальное дифференциальное звено
- •22.Реальное дифференцирующее звено.
- •23.Инерционное звено 1-го порядка.
- •24.Звенья второго порядка.
- •25. Звено с опаздываем.
- •26. Переходные процессы. Качественные показатели переходного процесса.
- •27. Интегральные оценки качества.
- •28. Методы коррекции автоматических систем.
- •29. Критерии Найквиста.
- •30. Критерий Михайлова.
- •31. Методы синтеза систем автоматического управления.
- •32.Синтез корректирующих устройств по логарифмическим частотным характеристикам.
- •33. Методы построения переходных процессов.
- •35. Основные виды нелинейности.
- •36. Метод фазового портрета.
- •37. Устойчивость нелинейных систем.
- •38. Метод гармонической линеаризации.
- •39. Метод Гольдфарба
- •40. Метод Попова.
- •41. Дискретные системы автоматического управления.
- •42. Виды модуляции в импульсных системах
- •43. Дискретное преобразование Лапласа. Z-преобразование.
- •44. Решетчатые функции ,разности, суммы функции, дифференциальные разностные уравнения.
- •4.1.1.1.2 Разностные уравнения.
- •45.Устоичивость импульсных систем.
38. Метод гармонической линеаризации.
Метод
гармонической линеаризации основан на
nредnоложении, что колебания на входе
нелинейного звена являются
синусоидальны.ми,т.
е. что
![]() ,
(12.1)
где А – амплитуда
и
,
(12.1)
где А – амплитуда
и ![]() -
частота этих автоколебаний , а
-
частота этих автоколебаний , а ![]() -
возможная в общем случае постоянная
составляющая, когда автоколебания
несимметричны.
Метод
гармонической линеаризации является
приближенным методом исследования
режима автоколебаний нелинейных систем.
Этим методом можно определить условия
возникновения и параметры автоколебаний,
как в системах второго порядка, так и в
более сложных системах.
-
возможная в общем случае постоянная
составляющая, когда автоколебания
несимметричны.
Метод
гармонической линеаризации является
приближенным методом исследования
режима автоколебаний нелинейных систем.
Этим методом можно определить условия
возникновения и параметры автоколебаний,
как в системах второго порядка, так и в
более сложных системах.
Метод
заключается в замене существенно
нелинейного элемента с
характеристикой ![]() эквивалентным
линейным звеном с коэффициентом
эквивалентным
линейным звеном с коэффициентом ![]() .
В замкнутой автоматической системе,
работающей в режиме автоколебаний,
условием эквивалентности служит
равенство амплитуд и фаз выходного
сигнала эквивалентного звена и первой
гармоники выходного сигнала реального
нелинейного элемента. При этом
предполагается, что сигнал на входе
нелинейного элемента является
синусоидальным. Такое предположение
справедливо во всех случаях, когда
линейная часть системы достаточно
инерционна и не пропускает высшие
гармоники.
.
В замкнутой автоматической системе,
работающей в режиме автоколебаний,
условием эквивалентности служит
равенство амплитуд и фаз выходного
сигнала эквивалентного звена и первой
гармоники выходного сигнала реального
нелинейного элемента. При этом
предполагается, что сигнал на входе
нелинейного элемента является
синусоидальным. Такое предположение
справедливо во всех случаях, когда
линейная часть системы достаточно
инерционна и не пропускает высшие
гармоники.
Пусть автоматическая система состоит из отделимых друг от друга линейной и нелинейной частей (см. рис. 8.1, а) и нелинейная часть описывается функцией (8.1). Предположим, что контур системы разомкнут (на выходе линейной части) и что на входе нелинейного элемента действует синусоидальный сигнал
|
(8.6) |
При этом
на выходе нелинейного элемента будет
возникать периодический сигнал ![]() ,
форма которого зависит от характера
нелинейности и в общем случае существенно
отличается от синусоидальной. Так, на
выходе двухпозиционного реле без зоны
нечувствительности (рис. 8.5, а)
образуется периодический сигнал
прямоугольной формы (рис. 8.5, б).
,
форма которого зависит от характера
нелинейности и в общем случае существенно
отличается от синусоидальной. Так, на
выходе двухпозиционного реле без зоны
нечувствительности (рис. 8.5, а)
образуется периодический сигнал
прямоугольной формы (рис. 8.5, б).
Уравнение (8.1) при синусоидальном воздействии можно записать в общем виде
|
(8.7) |
|
Периодический сигнал на выходе нелинейного элемента может быть разложен в ряд Фурье и тем самым представлен суммой гармонических составляющих:
|
(8.8) |
где
коэффициенты ![]() и
и ![]() определяются
известными формулами, а параметры
определяются
известными формулами, а параметры
|
(8.9) |
Для
нелинейных элементов с кососимметричной
относительно начала координат
характеристикой характерно наличие
постоянной составляющей ![]() и
отсутствие всех коэффициентов четных
гармоник, т.е.
и
отсутствие всех коэффициентов четных
гармоник, т.е. ![]() и
и ![]() .
.
При анализе замкнутой системы можно учитывать только первую гармонику и сигнал на выходе элемента с кососимметричной характеристикой приближенно представить так:
|
(8.10) |
Учитывая, что
|
(8.11) |
и вводя обозначения
|
(8.12) |
можно вместо (8.10) записать
|
(8.13) |
или в операторной форме
|
(8.14) |
При
выполнении указанных выше предпосылок
нелинейное уравнение (8.7) может быть
заменено линейным уравнением (8.13). Эта
процедура называется гармонической
линеаризацией,
а коэффициенты ![]() и
и ![]() – коэффициентами
гармонической линеаризации.
– коэффициентами
гармонической линеаризации.
Гармоническая линеаризация принципиально отличается от обычной линеаризации, так как коэффициенты гармонически линеаризованного элемента непостоянны и зависят от амплитуды входного сигнала. Эквивалентная прямолинейная характеристика (рис. 8.5, а – тонкая линия) имеет различный наклон при разных амплитудах входного сигнала.
Применение современных программных моделирующих систем позволяет исследовать любые нелинейные системы значительно точнее и быстрее, чем рассмотренными методами.

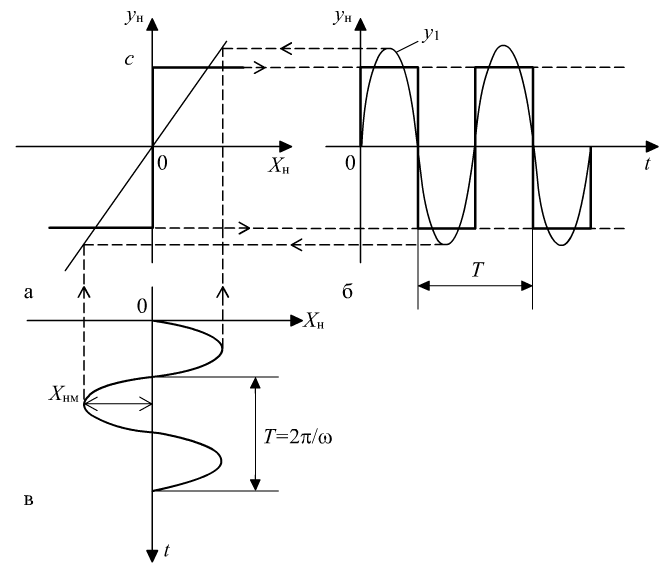 Рис.
8.5. Преобразование гармонического
сигнала нелинейным элементом
Рис.
8.5. Преобразование гармонического
сигнала нелинейным элементом