
- •Построение системы автоматического управления
- •Классификация систем автоматического управлении
- •Статистические характеристики элементов системы.
- •Статистические характеристики соединения звеньев.
- •Параллельное соединение звеньев
- •Последовательное соединение звеньев
- •Охват звена жесткой обратной связью
- •5. Виды статических ошибок (вывод формул).
- •6. Астатические элементы и системы.
- •Методы описания динамики линейных систем автоматического управления.
- •8. Классические методы решения дифференциальных уравнений
- •9. Операторные методы решения дифференциальных уравнений
- •10. Матричный метод решения уравнения.
- •11.Устоичивость автоматических систем.
- •12.Определение устойчивости по корням характеристического уравнения.
- •13.Теорема Ляпунова.
- •14. Частотные характеристики.
- •15. Логарифмические частотные характеристики.
- •16. Передаточные функции
- •17. Передаточные функции соединение звеньев.
- •18. Связь передаточных функций и частотных характеристик.
- •19.Типовые динамические звенья и их характеристики.
- •Типовые динамические звенья
- •20.Интегрирующее звено.
- •21.Идеальное дифференциальное звено
- •22.Реальное дифференцирующее звено.
- •23.Инерционное звено 1-го порядка.
- •24.Звенья второго порядка.
- •25. Звено с опаздываем.
- •26. Переходные процессы. Качественные показатели переходного процесса.
- •27. Интегральные оценки качества.
- •28. Методы коррекции автоматических систем.
- •29. Критерии Найквиста.
- •30. Критерий Михайлова.
- •31. Методы синтеза систем автоматического управления.
- •32.Синтез корректирующих устройств по логарифмическим частотным характеристикам.
- •33. Методы построения переходных процессов.
- •35. Основные виды нелинейности.
- •36. Метод фазового портрета.
- •37. Устойчивость нелинейных систем.
- •38. Метод гармонической линеаризации.
- •39. Метод Гольдфарба
- •40. Метод Попова.
- •41. Дискретные системы автоматического управления.
- •42. Виды модуляции в импульсных системах
- •43. Дискретное преобразование Лапласа. Z-преобразование.
- •44. Решетчатые функции ,разности, суммы функции, дифференциальные разностные уравнения.
- •4.1.1.1.2 Разностные уравнения.
- •45.Устоичивость импульсных систем.
25. Звено с опаздываем.
Звеном
запаздывания называется звено, передающее
сигнал со входа на выход без искажения
его формы, но с некоторой задержкой ![]() во
времени. Наиболее распространенным в
практике автоматических систем является
транспортное запаздывание, обусловленное
пространственным перемещением элементов,
передающих информацию (например,
транспортерная лента, полоса прокатываемого
металла). К статическим устройствам
запаздывания можно отнести различного
рода линии задержки электронного или
параметрического типа.
во
времени. Наиболее распространенным в
практике автоматических систем является
транспортное запаздывание, обусловленное
пространственным перемещением элементов,
передающих информацию (например,
транспортерная лента, полоса прокатываемого
металла). К статическим устройствам
запаздывания можно отнести различного
рода линии задержки электронного или
параметрического типа.
В некоторых случаях звено запаздывания вводится при расчете системы условно. Для ряда объектов уравнение динамики неизвестно, поэтому кривую переходного процесса реального объекта при единичном входном воздействии аппроксимируют экспонентой и эквивалентным запаздыванием.
Уравнение звена запаздывания
|
(3.64) |
не является дифференциальным и относится к классу особых уравнений со смещенным аргументом.
|
Подстановкой в уравнение звена значения входной величины получим его переходную функцию:
|
(3.65) |
а
подстановкой ![]() –
импульсную:
–
импульсную:
|
(3.66) |
Временные характеристики звена запаздывания показаны на рис. 3.8, а, б.
На основании теоремы запаздывания запишем уравнение (3.64) в изображениях по Лапласу:
|
(3.67) |
и определим передаточную функцию звена как
|
(3.68) |
А.ф.х. звена
|
(3.69) |
является окружностью единичного радиуса с центром в начале координат (рис. 3.8, е).
Амплитудная частотная и фазовая частотная характеристики определяются выражениями:
|
(3.70) |
|
(3.71) |
Звенья запаздывания ухудшают устойчивость систем и делают их трудно управляемыми.
Звено запаздывания определяет трансцендентный характер характеристического уравнения системы. Для приведения характеристического уравнения к алгебраической форме трансцендентную передаточную функцию звена раскладывают в ряд Пада и приближенно заменяют ее двумя или тремя членами ряда:
|
(3.72) |
или
|
26. Переходные процессы. Качественные показатели переходного процесса.
Переходный процесс — в теории систем представляет реакцию динамической системы на приложенное к ней внешнее воздействие с момента приложения этого воздействия до некоторого установившегося значения во временной области. Изучение переходных процессов — важный шаг в процессе анализа динамических свойств и качества рассматриваемой системы. Примерами внешнего воздействия могут быть дельта-импульс, скачок или синусоида.
Устойчивость системы автоматического регулирования является необходимым, но не достаточным условием ее практической пригодности. Понятие устойчивости отражает наличие или отсутствие затухания переходного процесса в системе. Его характер может быть самым разнообразным, кроме того, регулируемая величина может иметь различные отклонения от заданного значения в установившемся режиме. Возникает необходимость в оценке качества процессов в системе автоматического регулирования.
Существуют следующие показатели, характеризующие качество регулирования.
1. Длительность переходного процесса T — интервал времени с момента подачи ступенчатого входного сигнала до момента окончания переходного процесса. Переходный процесс закончен, если значение регулируемой величины отличается от заданного не более чем на 5 %.
2. Перерегулирование А — отношение максимального отклонения утах регулируемой величины к установившемуся фактическому значению ууст, выраженное в процентах:
Большое перерегулирование (выброс) вызывает чрезмерные силы в механических узлах и перенапряжения в электрических узлах систем автоматического регулирования, для большинства систем перерегулирование ограничено и составляет ст< (10...30) %, однако в некоторых системах допускается до 70 %, а в ряде случаев вообще может отсутствовать.
3. Статическая ошибка аст — отношение разности между заданным Уз и установившимся ууст значениями регулируемой величины к установившемуся значению, выраженное в процентах:
Статическая ошибка характеризует точность регулирования в установившемся режиме. В астатических системах стст = 0, а в статических не должна превышать 3... 5 %.
4. Частота колебаний в переходном процессе определяется числом колебаний регулируемого параметра за время переходного процесса. Обычно она равна 1,5 — 2.
Если качество процесса регулирования для заданных величин не удовлетворяет техническим требованиям (например, велико T, А, стст, недостаточный запас устойчивости и т. п.), то в систему дополнительно вводят параллельные корректирующие устройства (например, электрическую цепь) и выбирают их характеристики так, чтобы удовлетворить этим требованиям.
Параллельные корректирующие цепи включают в виде элементов отрицательной обратной связи, охватывающих наиболее инерционные звенья системы. В качестве параллельных стабилизирующих цепей чаще всего используют дифференцирующее звено для улучшения динамических свойств или интегрирующее звено для уменьшения статической погрешности.

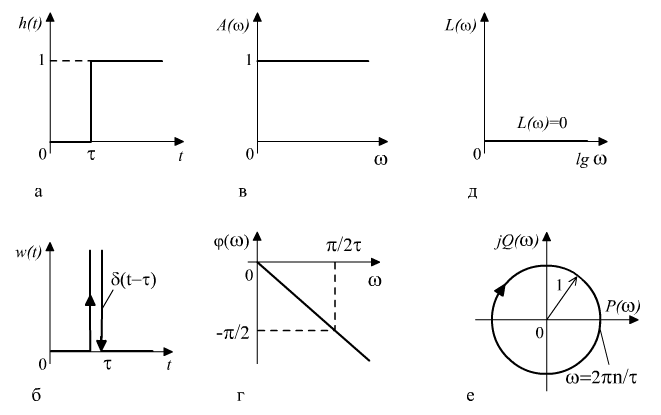 Рис.
3.8. Характеристики звена запаздывания
Рис.
3.8. Характеристики звена запаздывания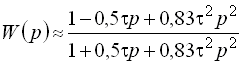 .
.