29. Моменты. Асимметрия и эксцесс.

Моментом к-го порядка называется среднее арифметическое из к-\ степеней отклонений значений признака от С

v.=(X",(^,-C)*)/n,

где X.—наблюдаемая варианта;«.—частота варианты; «=^ п. —

объем выборки; С—произвольное постоянное число.

Если С = О, то момент называется началъньш. Нетрудно заметить, что начальный момент первого порядка есть выборочная средняя

Если С = JC, то момент называется центральным порядка к

Нетрудно заметить, что центральный момент первого порядка равен нулю, а центральный момент второго порядка равен дисперсии.

Между центральными и начальными моментами существует зависимость

^з = Vз-Зv2Vl+2vJ^•

li,=v,-Av,v,+evy, -3v;.

Асимметрия распределения определяется равенством

а = 11^/а^

(аб]-оо,+оо[ )

И является показателем отклонения распределения признака X от симметрии относительно х. При а = О—распределение симметрично.

Эксцессом называется величина

г=^-3 (г€[-3,М)-

Эксцесс характеризует степень крутости кривой распределения признака X по сравнению с кривой нормального распределения. При в =0 — распределение нормально. Если г > О, то кривая распределения имеет более острую вершину, чем нормальное; если в < О — более плоскую вершину, чем нормальная кривая.

30. Биномиальное распределение.

Пусть выполнены все условия схемы независимых испытаний Бернулли.

Рассмотрим в качестве ДСВ X число появлений события A в этих испытаниях. Т. е. величина X может принимать значения: .

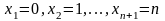Вероятности этих значений определяются по формуле Бернулли: , .

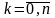Закон распределения вероятностей ДСВ X называется биномиальным, если вероятности ее возможных значений определяются по формуле Бернулли.

31. Пуассоновское распределение.

Пусть в схеме независимых испытаний Бернулли число испытаний достаточно велико (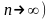 , а вероятность появления события A очень мала .

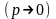Рассмотрим в качестве ДСВ X число появлений события A в этих испытаниях. Т. е. величина X может принимать значения: .

Вероятности этих значений определяются по формуле Пуассона: , .

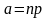Закон распределения вероятностей ДСВ X­ называется пуассоновским, если вероятности ее возможных значений определяются по формуле Пуассона.

32. Геометрическое распределение.

Пусть выполнены все условия схемы независимых испытаний. Испытания проводятся до 1-го появления события A. Т. е. если событие A появилось в k-м (катом) испытании, то в предыдущих k-1 испытаниях оно не появлялось.

Рассмотрим в качестве ДСВ X число испытаний, которые необходимо провести до 1-го появления события A. Т. о. возможные значения величины X: .

Вероятности этих значений определяются по формуле:

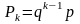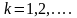, где . (1)

Если в эту формулу подставить последовательно вместо 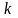: 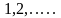, то получим геометрическую прогрессию с 1-м членом p и знаменателем q ( ) : .

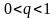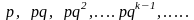Закон распределения вероятностей ДСВ X называется геометрическим, если вероятности ее возможных значений определяются по формуле (1) и образуют геометрическую прогрессию.