10. Теоремы сложения вероятностей.

Пусть даны два события A и B требуется определить вероятность появления хотя бы одного из этих событий.

Теорема Если события A и B несовместные, то вероятность появления одного из этих событий (сумма) равна сумме вероятностей данных событий, т.е. P(A+B)=P(A)+P(B)

Следствия:

Вероятность суммы нескольких несовместных событий A1,A2,…Ak равна сумме вероятностей этих событий, т. е. P(A1+A2+…+Ak)=P(A1)+P(A2)+P(A3)+….+P(Ak)

Если события A1,A2,…Ak образуют полную группу событий, то сумма их вероятностей равна единице.

Сумма вероятностей двух противоположных событий равна единице.

Теорема Если события A и B совместные, то вероятн появления хотя бы одного из этих событий (сумма) равна сумме вероятностей этих событий без вероятности их совместного появления, т. е. P(A+B)=P(A)+P(B)-P(AB)

11. Вероятность появления хотя бы одного события.

В некоторых случаях вероятность события удобнее подсчитывать как вероятность противоположного другому событию.

Пусть события A1,A2,…An попарно независимы и их вероятности известны и равны соответственно , тогда вероятности противоположных им событий будут равны .

Теорема Вероятность появления хотя бы одного из попарно независимых событий 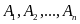равна разности между единицей и произведением вероятностей противоположных событий , т.е. .

12. Формула полной вероятно­сти.

Пусть имеется группа событий H₁, H₂,..., H_n, обладающая следую­щими свойствами:

1) все события попарно несовместны: H_i H_j =; i, j=1,2,...,n; ij;

2) их объединение образует пространство элементарных исходов :

 = 

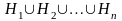
В этом случае будем говорить, что H₁, H₂,...,H_n образуют полную группу событий. Такие события иногда называют гипотезами.

П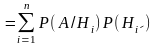 усть А – некоторое событие: А   (диаграмма Венна представлена на рисунке 8). Тогда имеет место формула полной вероятности:

P(A) = P(A/ H₁)P(H₁) + P(A/ H₂)P(H₂) + ...+ P(A/ H_n)P(H_n)

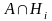Доказательство. Очевидно: A = , причем все события (i = 1,2,...,n) попарно несовместны. Отсюда по теореме сложения вероятностей получаем

P(A) = P( ) + P( ) +...+ P( ) Если учесть, что по теореме умножения P( ) = P(A/H_i)P(H_i) (i = 1,2,...,n), то из последней формулы легко получить приведенную выше формулу полной вероятности.

13. Вероятности гипотез. Формула Бейеса.

Пусть произведено испытание, в результате которого появилось событие A. Необходимо найти вероятности гипотез 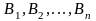, после того как испытание произведено, т. е. условные вероятности гипоте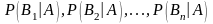 . Найдем сначала условную вероятность .

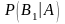По теореме умножения 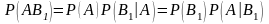. Отсюда .

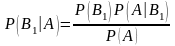Аналогично выводятся формулы остальных гипотез. В общем случае условная вероятность любой гипотезы , где 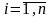, определяется как

Последняя формула называется формулой Байеса. Она позволяет переоценивать вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие A.

14. Схема независимых испытаний Бернулли.

При решении вероятностных задач часто приходится сталкиваться с ситуациями, в которых одно и тоже испытание повторяется многократно и исход каждого испытания независим от исходов других. Такой эксперимент еще называется схемой повторных независимых испытаний или схемой Бернулли.

Примеры повторных испытаний:

1) многократное извлечение из урны одного шара при условии, что вынутый шар после регистрации его цвета кладется обратно в урну;

2) повторение одним стрелком выстрелов по одной и той же мишени при условии, что вероятность удачного попадания при каждом выстреле принимается одинаковой (роль пристрелки не учитывается).

Итак, пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы; вероятность появления события А в каждом отдельно взятом или единичном испытании постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в одинаковых условиях). Обозначим вероятность появления события А в единичном испытании буквой р, т.е.  , а вероятность противоположного события (событие А не наступило) - буквой  .

Тогда вероятность того, что событие А появится в этих n испытаниях ровно k раз, выражается формулой Бернулли