20. Выборочный коэффициент ранговой корреляции Спирмена.

1. Выборочным коэффициентом ранговой корреляции Спирмена называется величина равная

,

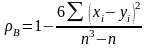где n - объем выборки.

Замечание 1. Значения коэффициента ранговой корреляции Спирмена расположены на отрезке .

21. Выборочный коэффициент ранговой корреляции Кендалла.

Выборочным коэффициентом ранговой корреляции Кенделла называется величина равная

.

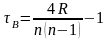Замечание 1. Значения коэффициентов ранговой корреляции Спирмена и Кенделла расположены на отрезке .

22. Виды статистических гипотез.

Статистической называют гипотезу о виде неизвестного распределения, или о параметрах известных распределений.

Нулевой (основной) называют выдвинутую гипотезу H0.

Если выдвинутая гипотеза будет отвергнута, то имеет место альтернативная гипотеза.

Конкурирующей (альтернативной) называют гипотезу H1, которая противоречит нулевой.

Простой называется гипотеза, если она состоит из одного предположения.

Сложной называется гипотеза, если она состоит из конечного или бесконечного числа простых гипотез.

23. Ошибки I и II рода.

Так как решение о справедливости гипотезы H0 принимается на основе выборочных данных, то могут возникнуть ошибки.

Ошибкой первого рода называется ошибка, состоящая в том, что гипотеза H0 отвергается, а на самом деле она верна.

Ошибкой второго рода называется ошибка, состоящая в том, что H0 принимается, а на самом деле она неверна.

24. Уровень значимости и мощность критерия.

Уровнем значимости называется вероятность 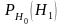совершить ошибку первого рода, т.е .

Замечание 1. Наиболее часто уровень значимости принимают равным 0,05 или 0,01.

25. Проверка гипотез о равенстве средних двух нормально распределенных генеральных совокупностей.

Пусть генеральные совокупности Х и У причем их дисперсии D(X) и D(Y) известны и по независимым выборкам, объемы которых равны n и m найдены выборочные средние

 

Нулевая гипотеза состоит в том, что:

Н0:М(Х)=М(У)

В этом случае в качестве критерия проверки нулевой гипотезы принимается случ величина

Z=

Критическая область строится в зависимости от вида конкурирующей гипотезы

Пусть конкурирующая гипотеза Н1: М(Х)<>M(Y)

Необходимо найти Zнаблюдаемое

 

|Zнаблюд|>Zкр

 

 Правило второе

Пусть конкурирующая гипотеза имеет вид

H1:M(X)>M(Y) 

Необходимо вычислить Zнаблюд

Если Zнаблюд > Zkp то нулевую гипотезу принимаем

26. Проверка гипотез о равенстве дисперссий двух нормально распределенных генеральных совокупностей.

Пусть по независимым выборкам, объемы которых n1 и n2, извлеченным из нормальных генеральных совокупностей, найдены исправленные выборочные дисперсии и .

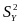Требуется по исправленным выборочным дисперсиям при заданном уровне значимости проверить нулевую гипотезу, состоящую в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой:

.

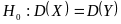В этом случае в качестве статистического критерия выбирается величина

.

Значения этого критерия находятся по таблице распределения Фишера – Снедекора.

Рассуждения строятся в зависимости от того, какой вид имеет конкурирующая гипотеза.

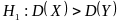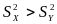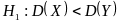Правило 1. Пусть конкурирующая гипотеза имеет вид , если или , если .

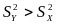1) Вычисляется .

2) По таблице критических точек распределения Фишера-Снедекора, по заданному уровню значимости и числам степеней свободы (n1 - объем выборки с большей исправленной выборочной дисперсией, а n2 - с меньшей) находится критическая точка .

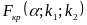3) Если - нет оснований отвергать нулевую гипотезу.

4) Если 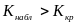- нулевую гипотезу отвергают.

Правило 2. Пусть конкурирующая гипотеза имеет вид .

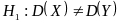Тогда все вычисления и выводы аналогичны правилу 1, с той лишь разницей, критическую точку 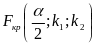ищут по уровню значимости вдвое меньшему заданного, т.е. .