46. Закон больших чисел и центральная предельная теорема (цпт).

Поскольку на практике сведения о каждой случайной величине, чаще всего, являются очень скромными и уверенно предсказать какое возможное значение она примет затруднительно, то может показаться, что нельзя установить закономерности поведения и суммы достаточно большого числа случайных величин. Оказывается, что это не так.

Закон больших чисел в широком смысле – это общий принцип, согласно которому совокупное действие большого числа случайных величин приводит, при некоторых сравнительно широких условиях, к результату, почти независящему от случая, т.е. при большом числе случайных величин их средний результат перестает быть случайным и может быть предсказан с большой степенью

47. Неравенство Чебышева. Теорема Чебышева.

Если случайная величина X принимает только неотрицательные значения, то для любого числа выполняется неравенство: .

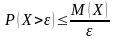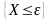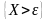Для события , противоположного событию , неравенство Маркова может быть записано в виде:

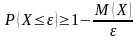
Теорема 2. (неравенство Чебышева)

Вероятность того, что отклонение случайной величины X от ее математического ожидания по абсолютной величине меньше любого числа , не меньше чем 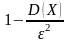, т.е. .

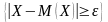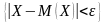Для события , противоположного событию , неравенство Чебышева может быть записано в виде: .

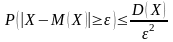Теорема 3. (теорема Чебышева) Если - попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышают постоянного числа C), то, как бы мало ни было , вероятность неравенства:

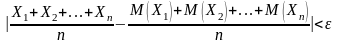
будет как угодно близка к единице, если число случайных величин достаточно велико.

Замечание 1. Теорема Чебышева утверждает, что если рассматривается достаточно большое число случайных величин, имеющих равномерно ограниченные дисперсии и являющиеся независимыми, то почти достоверным можно считать событие, состоящее в том, что отклонение среднего арифметического случайных величин от среднего арифметического их математических ожиданий будет по абсолютной величине сколь угодно малым.

(частный случай теоремы Чебышева)

Если - попарно независимые случайные величины, имеющие одинаковые математические ожидание a, и их дисперсии равномерно ограничены (не превышают постоянного числа C), то, как бы мало ни было , вероятность неравенства:

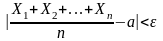
будет как угодно близка к единице, если число случайных величин достаточно велико.

48. Теоремы Бернулли и Пуассона.

(теорема Бернулли) Если в каждом из n независимых испытаний вероятность p события A постоянна, то вероятность того, что отклонение относительной частоты от вероятности p по абсолютной величине будет сколь угодно малым, будет как угодно близка к единице если число испытаний достаточно велико, т.е.

.

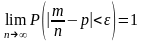Сущность теоремы Бернулли: теорема Бернулли позволяет предвидеть, какова примерно будет относительная частота появления события.

49. Массовые случайные явления и цпт.

Предельные законы распределения составляют предмет другой группы теорем - центральной предельной теоремы, которую иногда называют «количественной формой закона больших чисел».

Все формы центральной предельной теоремы посвящены установлению условий, при которых возникает нормальный закон распределения, Так как эти условия на практике весьма часто выполняются, формальный закон является самым распространенным из законов распределения, наиболее часто встречающимся в случайных явлениях природы. Он возникает во всех случаях, когда исследуемая случайная величина может быть представлена в виде суммы достаточно большого числа независимых (или слабо зависимых) элементарных слагаемых, каждое из которых в отдельности сравнительно мало влияет на сумму.

Сумма элементарных отклонений:

,            

где   - отклонения, вызванные отдельными факторами.

Так как этих факторов очень много, между собой они являются в основном независимыми и по влиянию на сумму отдельные слагаемые можно считать приблизительно равномерно малыми, то налицо условия применимости центральной предельной теоремы, и величина должна подчиняться закону распределения, близкому к нормальному.