Теория вероятностей

1. Правила комбинаторики.

1) Комбинаторика изучает количества комбинаций, подчиненных опеределенным условиям, которые можно составить из элементов заданного конечного множества.

Правила комбинаторики.

Пусть А1, А2,..., Аk - это элементы заданного конечного множества.

Правило суммы. Если элемент А1 можно выбрать n1 способами, А2 можно выбрать n2 способами и т.д. Аk можно выбрать nk способами, отличными от всех предыдущих, то выбор одного из элементов А1, А2,..., Аk может быть осуществлен n1+n2+...+nk способами.

Правило произведения. Пусть элемент А1 можно выбрать n1 способами, после каждого такого выбора элемент А2 можно выбрать n2 способами и т.д. После k-1 -го выбора элемент Аk можно выбрать nk способами, тогда выбор всех элементов А1, А2,...,Аk в указанном порядке может быть осуществлен n1*n2*...*nk способами.

2. Основные комбинаторные соединения: перестановки, размещения, сочетания.

Пусть дано множество из n элементов. Из этого множества могут быть составлены подмножества (комбинации) по m элементов (0=<m=<n) трех основных видов: перестановки, размещения и сочетания.

Перестановки (m=n)

Перестановками без повторения называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их следования. Число всевозможных перестановок без повторений Pn=n!

Размещение и сочетание (м<n)

Размещениями без повторений называют комбинации, составленные из n различных элементов по m элементов,которые отличаются либо составом элементов, либо порядком следования. Число всевозможных размещений и повторений: Аm/n=n!/(n-m)!

Сочетаниями без повторения называются комбинации из n различных элементов по m элементов, которые отличаются только составом. Число сочитаний Без поВторений Сm/n=n!/(m!*(n-m)!)

Свойства сочетаний:

С0/n=1

C1/n=n

Cn/n=1

3. Испытание. Событие. Классификация событий.

Испытание- это многократное воспроизведение одного и того же комплекса условий, при котором проводится наблюдение

Событие- качественный результат испытания

Случайным событием называется событие, которое при осуществлении некоторых условий может произойти или не произойти.

-Событие называется достоверным, если в результате испытания оно обязательно происходит. 

-Невозможным называется событие, которое в результате испытания произойти не может.

-Два события называются совместными, если при одном испытании появление одного из них не исключает появление другого.

-Два события называются несовместными, если при одном испытании появление ожного из них исключает появление другого.

-Несколько событий образуют полную группу в данном исспытании, если они попарно несовместимы и в результате испытания одно из этих событий обязательно появится.

-Два несовместных события, образующих полную группу, называютя противоположными.

-События называютя равновозможными, если есть основание считать,что одно из них не ялвляется более возможным, чем другое.

4. Понятие вероятности события. Классическое определение вероятности и его свойства.

Вероятность события- численная мера степени объективной возможности наступления события в данном испытании.

Свойства вероятностей:

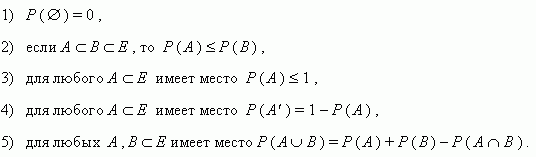
1.вероятность достоверного события=1

Р(А)= n/n

2. вероятность невозможного события = 0

P(A)= 0/n

3. вероятность случайного события есть положит. число, закльное между 0 и 1

0<= m/n<=1