49.Файлы, работа с файлами исходных данных и результатов на пк.

1. Физические и логические файлы.

Типы файловых переменных.

Физическим файлом мы называем единую именованную область данных на диске. Физический файл определяется строкой с его именем и путем к нему.

Например:

d:\work\doc\mywork.doc - файл с именем "mywork" и расширением "doc" находится в подкаталоге "doc" каталога "work" на диске "d:".

Логический файл в Паскале описывается как переменная одного из файловых типов.

Мы связываем логический файл с физическим файлом на диске и через логический получаем доступ к физическому. В Паскале существует три типа файловых переменных: текстовые файлы (тип Text); компонентные или типизированные файлы (тип File of...); бестиповые или нетипизиованные файлы (тип File). Текстовый файл, с которым мы работаем в DOS-среде, состоит из последовательности ASCII-кодов, среди которых могут быть и управляющие.

2. Основные операции работы с файлами

1) Assign (var FileVar; FileName : string)

Эта директива связывает файловую переменную FileVar с именем физического файла, заданным в строке FileName. Таким образом, все операции, которые мы будем проделывать с переменной FileVar, на самом деле будут изменять физический файл с именем FileName.

Эта связь сохранится до следующего вызова assign с той же переменной FileVar.

2) Reset (var FileVar) и Rewrite (var FileVar)

Процедура Reset открывает файл FileVar для чтения.Процедура Rewrite открывает файл FileVar для записи.

3) Close (var FileVar)

Так мы закрываем файл. При этом связь между файловой переменной и физическим файлом не теряется, но текущее состояние файла - "закрыт".

При закрытии файла все данные из памяти дописываются в него.

51. Численное интегрирование, постановка задачи.

Задача численного интегрирования состоит в замене исходной подинтегральной функции f(x), для которой трудно или невозможно записать первообразную в аналитике, некоторой аппроксимирующей функцией φ(x). Такой функцией обычно является полином (кусочный полином) . То есть:

где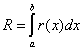 – априорная погрешность метода на интервале интегрирования,

а r(x) – априорная погрешность метода на отдельном шаге интегрирования.

Численное интегрирование (историческое название: (численная) квадратура) — вычисление значения определённого интеграла (как правило, приближённое). Под численным интегрированием понимают набор численных методов отыскания значения определённого интеграла.

Численное интегрирование применяется, когда:

Сама подынтегральная функция не задана аналитически. Например, она представлена в виде таблицы (массива) значений в узлах некоторой расчётной сетки.

Аналитическое представление подынтегральной функции известно, но её первообразная не выражается через аналитические функции. Например, .

В этих двух случаях невозможно вычисление интеграла по формуле Ньютона-Лейбница. Также возможна ситуация, когда вид первообразной настолько сложен, что быстрее вычислить значение интеграла численным методом.