Контрольні питання

1. Визначення передавальної та приймальної антени.

2. Структура антени.

3. Класифікація антен.

4. Принцип суперпозиції в теорії антен.

5. Принцип двоїстості.

6. Теорема еквівалентності.

7. Принцип розрахунку потужності випромінювання антени.

8. Поняття про зони випромінювання.

9. Параметри, що характеризують ефективність перетворення енергії в/ч струмів антени в енергію електромагнітних хвиль.

10. Що таке діаграма направленості антени?

11. Способи подання діаграми направленості антени.

12. Параметри, що визначаються з діаграми направленості антени.

13. Визначення коефіцієнта направленої дії антени.

14. Що таке коефіцієнт підсилення антени?

15. Який зв'язок між конструктивними та електричними параметрами антени?

16. Що таке елементарний випромінювач?

17. Диполь Герца та його характеристики.

18. Елементарний магнітний випромінювач та його технічна реалізація.

19. Поняття про елементарний щілинний випромінювач.

20. Елемент Гюйгенса та його характеристики.

21. Що таке лінійна випромінююча система?

22. 3а яким принципом визначається діаграма направленості лінійної випромінюючої системи?

23. Що таке еталонна лінійна випромінююча система і для чого вона використовується?

24. Якою функцією описується діаграма направленості еталонної лінійної випромінюючої системи?

25. 3а яких умов виникає режим поперечного випромінювання?

26. За яких умов виникає режим похилого випромінювання? Яким способом здійснюється сканування навколишнього простору?

27. За яких умов виникає режим осьового випромінювання?

28. Дати оцінки параметрів випромінювання для різних режимів роботи.

29. Як впливає нерівномірний розподіл струмів на характеристики антени?

30. 3а яким принципом визначається діаграма направленості поверхневої

випромінюючої системи?

31. Від чого залежить гострота головного пелюстка діаграми направленості

поверхневої випромінюючої системи?

32. Від чого залежить коефіцієнт направленої дії поверхневої випромінюючої системи?

33. У чому полягає суть методу визначення діаграми направленості довільної антени?

34. Поняття про антенну решітку.

Література

1. Г.Т.Марков, Д.М.Сазонов. Антенньї. - М.: «Знергия», 1975. - 528 с.

2. Антенньі и устройства СВЧ. (Проектирование фазированньїх антенньїх решеток). /Под ред. Д.И.Воскресенского. - М.: «Радио и связь», 1981. - 432 с.

З. Г.З.Айзенберг, В.Г.Ямпольский, О.Н.Терешин. Антенньї УКВ, т.1, т.2. -М.: «Радио и связь», 1977. -384 с, -288 с. 4.Г.Н.Кочержевский. Антенно-фидерные устройства.-М.: «Связь», 1968.-480с

2. Розрахунок рупорних антен

2.1. Теоретична частина.

Рупорні антени відносяться до класу антен з випромінюючою поверхнею (апертурою). До найпростіших випромінювачів такого типу підноситься відкритий кінець прямокутного хвилеводу, по якому поширюється основна хвиля типу Н10. Структура поля у поперечному перерізі та амплітудний розподіл складових поля по широкій а та вузькій b стінкам хвилеводу подані нарис.2.1.

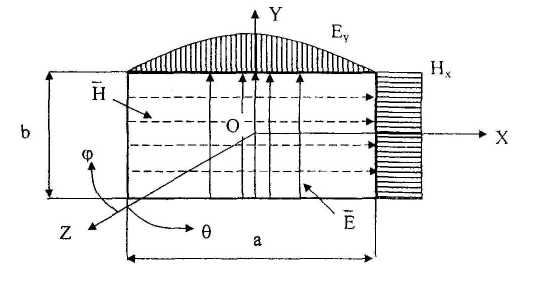
Рис.2.1 .Структура та розподіл поля у поперечному перерізі прямокутного хвилевода.

На середній частоті робочого діапазону для реалізації однохвильового режиму необхідно забезпечити наступні співвідношення між поперечними розмірами хвилеводу та довжиною хвилі:

а = (0,7...0,80* , b = (0,35...0,40)* (1 )

За методикою, що використовується у теорії лінійних випромінюючих систем, випромінююча поверхня з розміром а х b представляється у вигляді системи елементарних прямокутних випромінювачів - випромінювачів Гюйгенса, і результуюче поле у будь-якій точці простору знаходиться шляхом сумування полів від окремих випромінювачів (принцип суперпозиції) (рис.2.2).

Рис.2.2. Представлення випромінюючої поверхні у вигляді

системи елементів Гюйгенса.

За цією ж методикою можна виконати оцінку параметрів направленості такого випромінювача:

- коефіцієнта направленої дії - D=K_ВП*D₁*D_X*D_Y,

де K_ВП - коефіцієнт використання поверхні розкриву. Для поданого на рис.1 амплітудного розподілу поля K_ВП ⁼ 0,81;

D₁ - КНД елемента Гюйгенса. D₁ = 

D_X - КНД лінійної випромінюючої системи, елементи якої розташовані вздовж осі X. D_X = 2*а / ;

D_Y — КНД лінійної випромінюючої системи, елементи якої розташовані вздовж осі Y. D_Y = 2*b / .;

звідси: D = 0,81- ; (2)

-оцінка гостроти головного пелюстка діаграми направленості у площинах ХOZ та YOZ виконується за виразами:

=К_РП1*51⁰* , = К_РП2*51⁰*

де К_РП1 та К_РП2 - відповідні коефіцієнти розширення проміню, що враховують амплітудний розподіл поля по координаті. Для косинусоїдного розподілу поля К_РП1 = 1,31, для рівномірного розподілу поля К_РП2 = 1.

Оцінки направленості випромінювання за наведеними співвідношеннями показують низький КНД (D3) та значну ширину головного пелюстка діаграми (90⁰, 135⁰) для випромінювача у вигляді відкритого кінця хвилеводу. Ефективним засобом покращення цих характеристик могло би бути збільшення розмірів поперечного перерізу хвилеводу, однак це призводить до виникнення вищих типів хвиль і порушення умови синфазності поверхні випромінювання. Для ілюстрації на рис.З наведений розподіл електричного поля у хвилеводі для хвилі H₂₀, яка виникає при двократному збільшенні розміру а.

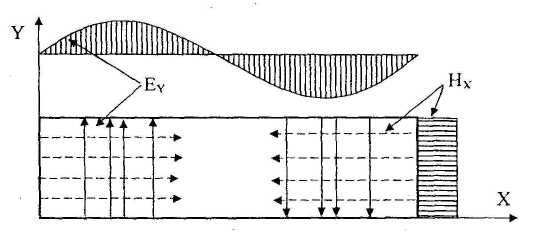
Рис.2.З. Структура та розподіл поля для хвилі H₂₀.

Легко побачити, що ліва та права половина хвилеводу збуджуються протифазно, що ліквідує випромінювання у напрямку осі хвилеводу (осі Z). У цьому випадку діаграма направленості стає багатопелюстковою, а КНД знижується. Виходом з цієї ситуації є поступове збільшення розмірів поперечного перерізу хвилеводу зі збереженням основного типу хвилі. Таким чином ми приходимо до антен, які одержали назву рупорних. У конструктивному плані існує кілька різновидів рупорних антен: Н-секторійний рупор, де в площині магнітного поля Н відбувається поступова зміна розміру а до а_Р (рис.4,а), Е-секторійний рупор, де в площині електричного поля Е відбувається поступова зміна розміру b до b_Р (рис.4,6), пірамідальний рупор, де відбувається одночасне збільшення розмірів до а_Р та b_Р(рис.4,в), і, нарешті, конічний рупор, виконаний аналогічним чином, але на основі круглого хвилеводу (рис.4,г).

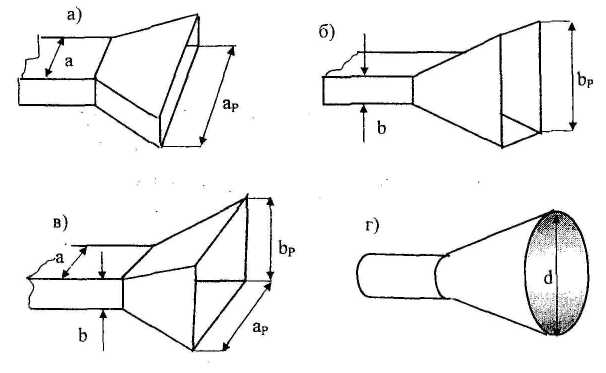
Рис.2.4. Основні конструктивні різновиди рупорів.

Структура поля у розкриві рупора відповідає структурі поля у хвилеводі. Основна відмінність поля у розкриві рупора від поля хвилеводу полягає у тому, що фронт хвилі перестає бути плоским, а стає циліндричним (у секторійних рупорах) або близьким до сферичного (у пірамідальному та конічному рупорі). Це можна легко показати побудовою структури поля у поздовжньому перерізі Е-секторійного рупора (рис.5).

Рис.2.5. Структура поля у поздовжному перерізі Е-секторійного рупора.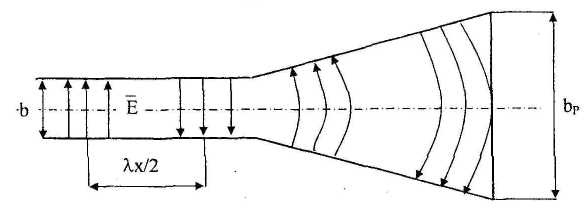

Форма силових ліній електричного поля у рупорі відповідає умові їх ортогональності до стінок рупора згідно з граничними умовами для електричного поля на провідних поверхнях (рис.2.5). Це означає, що силові лінії, а також фронт електромагнітної хвилі співпадають з утворюючими циліндра, вісь якого знаходиться на перетині продовження стінок рупора (вісь О на рис.2.6).

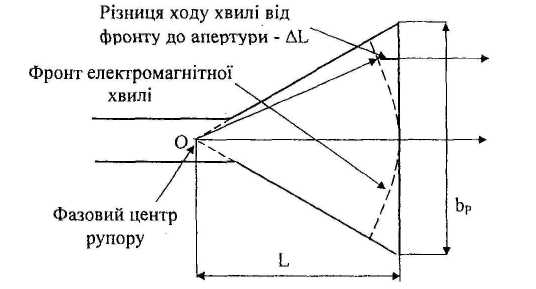
Рис.2.6. Утворення циліндричної хвилі з фазовим центром О.

Оскільки поверхня циліндра не співпадає з плоскою поверхнею апертури рупору, то різниця фаз для елементарних випромінювачів, розташованих на площині, визначається різницею хода хвиль від фазового центра О до апертури (L на рис.2.6). Залежність різниці фаз від координати точки на апертурі визначається наступним виразом:

Ф(х)= ,рад (4)

Для наближеної оцінки максимального фазового спотворення використовується вираз:

Ф_МАХ

Збільшення розкриву рупора підвищує КНД, однак, одночасно зростають фазові спотворення, які протидіють цьому. Існують допустимі фазові спотворення на краях рупора, при яких КНД досягає максимальної величини: _МАХ=/2 - для Н-секторійного рупора, _МАХ =3- / 4 - для Н-секторійного та конічного рупора. Рупор, у якого відношення розкриву до його довжини відповідає умові максимального КНД, називають оптимальним:

- для Е-секторійного рупора - L_Еopt= (6)

-для Н-секторійного рупора - (7)

-для конічного рупора- (8)

За формулами (6), (7) розраховується оптимальна довжина пірамідального рупора. КНД для оптимального пірамідального рупора оцінюється виразом:

(9)

де S = a_Рb_Р - площа розкриву пірамідального рупора,

Квп ⁼ 0,49 - коефіцієнт використання поверхні розкриву, що враховує нерівномірність амплітудного розподілу та фазові спотворення.

За цим же виразом оцінюються КНД для секторійних рупорів. Для конічного рупора, збудженого хвилею Н₁₁ КНД розраховується за формулою:

D= (10)

Діаграми направленості рупорів з прямокутним розкривом розраховуються за формулами:

-у площині Н: F()= (11)

де ()=a_psin()/; ()=b_psin()/ - узагальнені кутові змінні.

Для конічного рупора розрахунок діаграми направленості ведеться за формулою:

F()= (13)

де J₁ - функція Беселя першого порядку від аргументу (dsin/).

Оцінка ширини головного пелюстка на рівні -3 дБ для рупорів з прямокутним та круглим розкривом виконується за формулами:

, ,

Пірамідальні та конічні рупори характеризуються хорошим узгодженням з хвилеводним трактом, оскільки являють собою плавні переходи від хвильового опору хвилеводу до хвильового опору вільного простору. Робоча смуга частот рупорних антен визначається робочою смугою під'єднаних до них хвилеводів. Позитивними рисами рупорних антен є простота конструкції та технологічність. Для виготовлення рупорів використовуються листовий алюміній або сталь з відповідним антикорозійним захистом. Для забезпечення необхідної жорсткості конструкції на зовнішній стороні рупора встановлюється арматура з профільованих матеріалів. Для захисту від дії атмосферних умов на виході рупора встановлюють кришки з пінополістиролу.

Рупорні антени з КНД = 10...5-10² широко використовуються у вимірювальній техніці завдяки їх простоті та можливості забезпечення еталонних параметрів. Створення рупорних антен з високим КНД наштовхується на конструктивні труднощі, тому що зі збільшенням розкриву рупора його довжина зростає квадратично. Тому для досягнення високих КНД використовуються комбіновані антени, де рупорні грають роль опромінювачів.