3.2. Соединение элементов трехфазной цепи треугольником.

Такое соединение получается, если три фазы приемника с комплексными сопротивлениями включить между линейными проводами

(рис. 15.7, а). При таком соединении фазные напряжения приемника равны линейным напряжениям генератора, т. е. Постоянство линейных напряжений обеспечивает такую же независимость режима работы отдельных фаз, как и в схеме рис.15.5.

Для рассматриваемой цепи токи фаз приемника определяются по формулам:

(15.7)

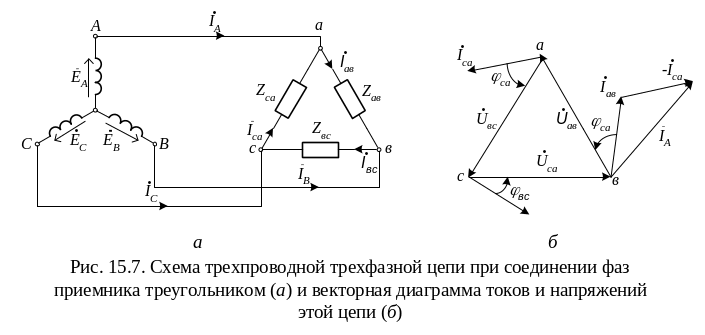
В отличие от соединения звездой при соединении треугольником фазные токи не равны линейным. Линейные токи можно определить по фазным, составив уравнения по первому закону Кирхгофа для узлов а, в и с (рис. 15.7, а):

(15.8)

С помощью этих уравнений можно определить линейные токи графически, воспользовавшись векторной диаграммой фазных токов (рис. 15.7, б). Если приемник симметричный, то векторы фазных токов образуют симметричную систему, в которой значения фазных токов и сдвиги фаз между токами и соответствующими фазными напряжениями одинаковы. Из векторной диаграммы рис. 15.7, б следует, что в случае симметричных приемников

(15.9)

Важной особенностью трехпроводной цепи является то, что независимо от характера приемников геометрическая сумма линейных токов равна нулю:

4. Мощность трехфазных цепей

Мгновенная мощность трехфазного источника электрической энергии равна сумме мгновенных мощностей каждой фазы:

р = р_А + р_В + р_С =u_A ∙ i_A + u_B ∙ i_B +u_C ∙ i_C.

Под активной мощностью трехфазной системы понимают сумму активных мощностей фаз и активной мощности, выделяемой на сопротивлении нулевого провода:

(15.10)

Реактивная мощность – это сумма реактивных мощностей фаз нагрузки и реактивной мощности сопротивления нулевого провода:

(15.11)

Полная мощность

. (15.12)

Если нагрузка равномерная, то

Тогда

(15.13)

. (15.14)

Здесь индексом  обозначается угол между напряжением U_Ф и током I_Ф фазы нагрузки.

При равномерной нагрузке фаз выражения (15.12) ÷ (15.14) имеют вид:

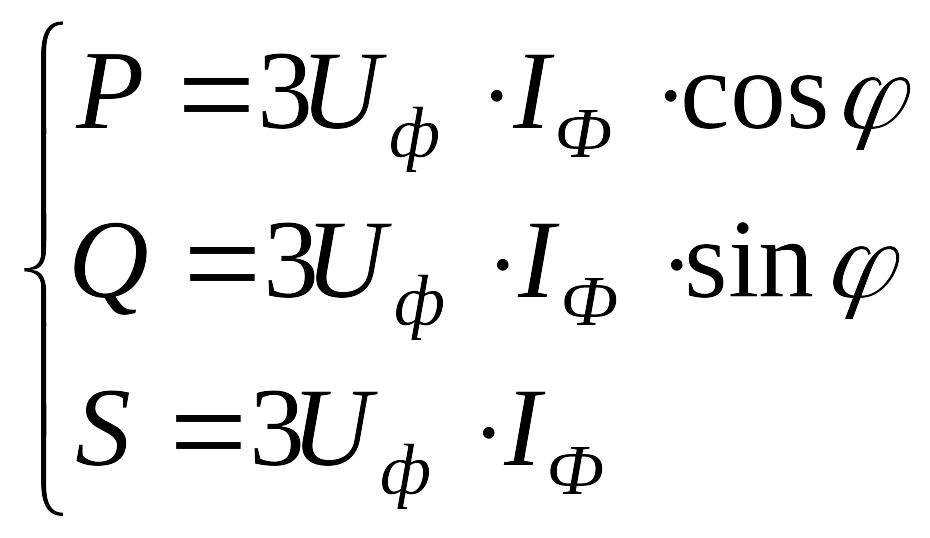. (15.15)

При равномерной нагрузке независимо от способа ее соединения в "звезду" или в "треугольник" справедливы равенства:

.

Поэтому вместо формул (15.15) используют следующие:

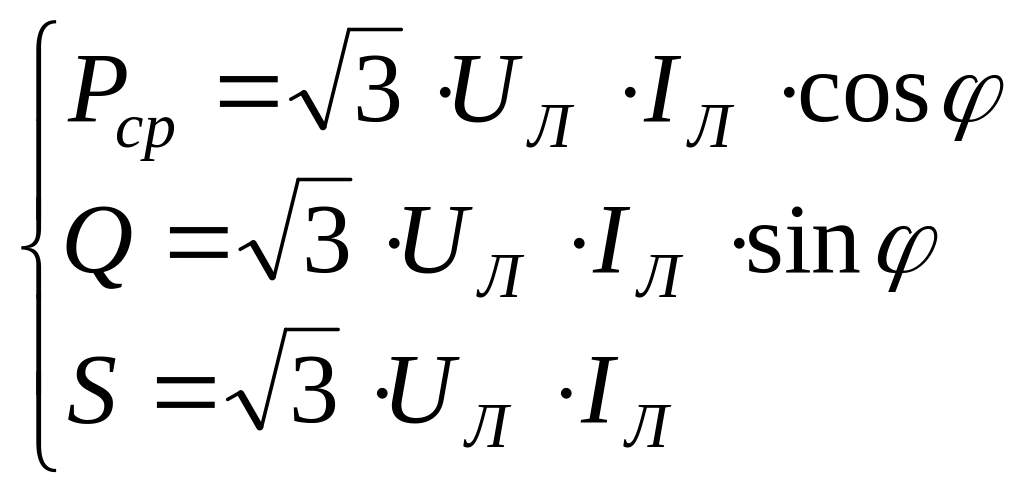. (15.16)

Для измерения мощности в трехфазных цепях в общем случае необходимо три ваттметра включить по схеме рис 15.8, а.

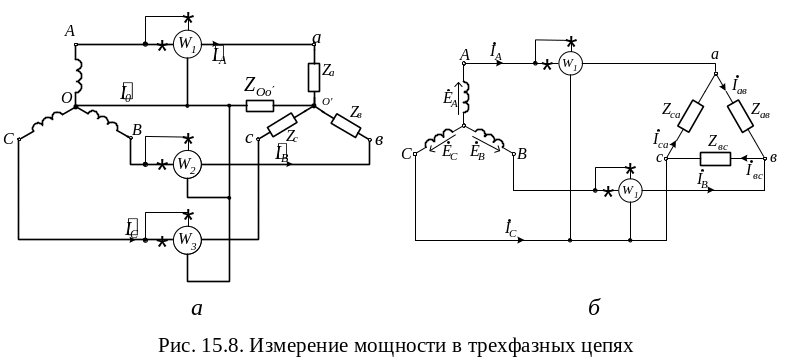
Активная мощность системы равна сумме показаний трех ваттметров.

Если нулевой провод отсутствует, то измерение мощности производят по методу Арона (рис.15.8, б). При симметричной нагрузке сумма показаний ваттметров равна активной мощности цепи:

Р₁ + Р₂ = 3 U_л·I_л·cos φ,

разность показаний ваттметров равна реактивной мощности цепи:

Р₁ - Р₂ = U_л·I_л·sin φ.

Выражение для определения φ имеет вид:

φ = arc tg [3(P₁ – P₂)/(P₁ + P₂)].