3.Частотная характеристика двухполюсника

В общем случае входное сопротивление и входная проводимость двухполюсника являются функцией частоты. Зависимости действительной и мнимой частей входного сопротивления или входной проводимости двухполюсника от частоты называют частотными характеристиками двухполюсника.

Частотные характеристики либо рассчитывают, когда известна схема цепи и значения элементов в ней, либо снимают опытным путем. Наибольший интерес представляют частотные характеристики двухполюсников, составленных только из индуктивностей и емкостей. Если частота источника питания достаточно высока, то активные сопротивления катушек индуктивности оказываются пренебрежимо малыми по сравнению с их индуктивными сопротивлениями. Ими можно пренебречь. Тогда получаем идеализированную упрощенную схему только из индуктивностей и емкостей. Построение частотных характеристик таких схем значительно упрощается.

Рассмотрим построение частотных характеристик двухполюсников, приведенных на рис. 12.7, а и г.

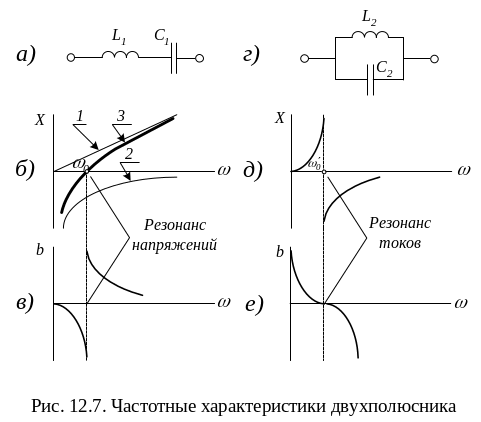
При построении будем полагать элементы схем идеальными, т. е. не имеющими потерь энергии. Входное сопротивление и входная проводимость для двухполюсника рис. 12.7, а равны:

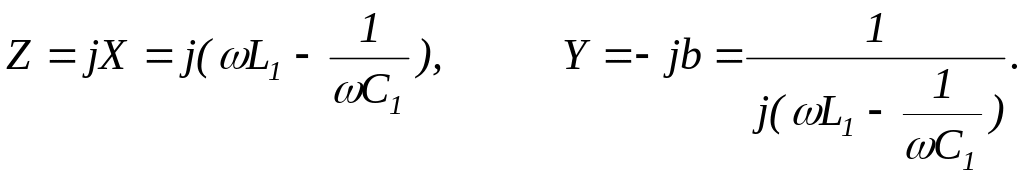
На рис. 12,7, б график 1 определяется зависимостью , график 2 – зависимостью , а график 3 – зависимостью .

Значение ω = ω₀, при котором график 3 пересекает ось абсцисс, определяет резонансную частоту в цепи рис. 12.7, а (резонанс напряжений). При входное сопротивление имеет емкостной характер (Х отрицательно), при – индуктивный (Х положительно).

График зависимости приведен на рис. 12.7, в. При входная проводимость имеет емкостной характер, при – индуктивный. В точке график зависимости претерпевает разрыв от - ∞ до + ∞.

Для двухполюсника рис. 12.7, г входная проводимость и входное сопротивление соответственно равны:

Зависимости и изображены соответственно на рис. 12.7, д и е. При реактивная проводимость b становится равной нулю, а реактивное сопротивление Х претерпевает разрыв от + ∞ до - ∞. При в двухполюснике рис. 12.7, г имеет место резонанс токов.

Таким образом, по виду зависимостей и можно судить о типе резонансных режимов, которые будут возникать при изменении частоты от + ∞ до - ∞.

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ

12.1. Объясните, чем определяется характер сопротивления электрической цепи синусоидального тока и как его можно изменять.

12.2. Сформулируйте определение резонанса цепи. Назовите виды резонанса, приведите их отличительные признаки и общие свойства.

12.3. Приведите выражения для добротности параллельного и последовательного колебательных контуров. Чем отличаются эти выражения?

12.4. В схеме рис. 12.1 известно: е(t) = 14,1 sin 314 t, R = 200 Ом, а L = 0,1 Гн. Определите значение емкости, при котором в цепи возникнет резонанс.

12.5. По данным задачи 12.4 определите добротность цепи рис. 12.1, общий ток цепи, а также токи ее ветвей.

12.6. Используя данные задачи 12.5, определите полную, активную и реактивную мощность цепи по схеме рис. 12.1. Сформулируйте предложение по способу увеличения коэффициента мощности цепей синусоидального тока.

12.7. Сформулируйте определение характеристического сопротивления.

12.8. В схеме рис. 12.5 известно: е(t) = 14,1 sin 314 t, R = 4,9 Ом, а L = 0,1 Гн. Определите значение емкости, при которой в цепи возникнет резонанс.

12.9. По данным задачи 12.8 определите добротность цепи рис. 12.5, общий ток цепи, а также падение напряжения на R, L и С элементах. Сравните полученные результаты с результатами задачи 12.5. Назовите параметры цепей, имеющие одинаковые и различные значения.

ЛЕКЦИЯ 13. ЭЛЕКТРЧЕСКИЕ ЦЕПИ С ВЗАИМНОЙ