Применим к (11.19) выражение (11.7), тогда

. (11.20)

Коэффициент

[вар] (11.21)

называется реактивной мощностью, обозначается Q и измеряется в вольт-амперах реактивных [вар].

Теперь общее выражение для мгновенной мощности всей цепи

(рис.10.1) можно записать в виде

. (11.22)

Второе и третье слагаемые в (11.22) свернем как косинус суммы двух аргументов –cos(2ωt+φ). Тогда выражение (11.22) приходит к виду

. (11.23)

Таким образом, мгновенная мощность цепи содержит постоянную и переменную составляющие. Переменная составляющая мгновенной мощности изменяется относительно постоянной с удвоенной частотой (рис. 11.4). Графики рис. 11.4 иллюстрируют фазовые соотношения между мгновенными значениями тока i(t), напряжения u(t) и мощности p(t). Амплитудное значение переменной составляющей в (11.23) обозначают S и называют полной мощностью цепи:

[ВА]. (11.24)

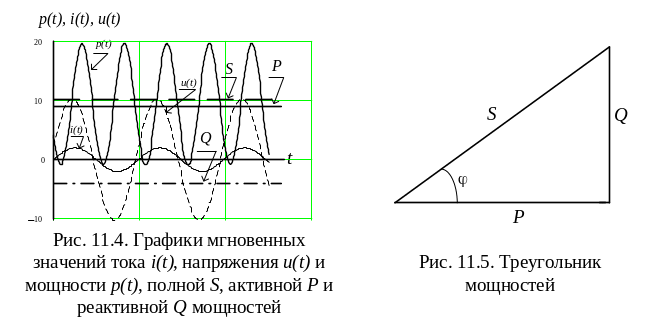
Полная мощность в cosφ раз превышает постоянную составляющую (активную мощность). Поэтому график мгновенной мощности заходит в

область отрицательных значений. Величина области отрицательных значений определяется коэффициентом мощности. Физически эта область определяет моменты времени, в которые цепь возвращает энергию источнику.

Следует учитывать тот факт, что полная и активная мощности явля-ются арифметическими величинами, а реактивная мощность – величина алгебраическая. Когда индуктивное сопротивление цепи по абсолютной величине больше емкостного, разность фаз между током и напряжением положительна – φ > 0. Поэтому Q = U ∙ I ∙ sinφ >0.

Когда большей оказывается величина емкостного сопротивления, реактивная мощность становится отрицательной. Именно такой вариант соотношения реактивных сопротивлений в цепи рис. 10.1 отражают графики рис. 11.4. Они рассчитаны для следующих значений величин: i(t) = 2 ∙ sin(314 ∙ t), R = 5 Ом, L = 0,5 Гн, С = 20 мкФ.

Если умножить все стороны треугольника сопротивлений (рис. 10.2) на , то получим треугольник мощностей (рис.11.5). В этом треугольнике гипотенуза эквивалентна полной мощности – S, прилежащей к острому углу катет – активной мощности Р, а противолежащий – реактивной мощности Q. Угол φ определяется сдвигом фаз между током и напряжением цепи и задает значение коэффициента мощности. Для треугольника очевидны соотношения:

(11.25)

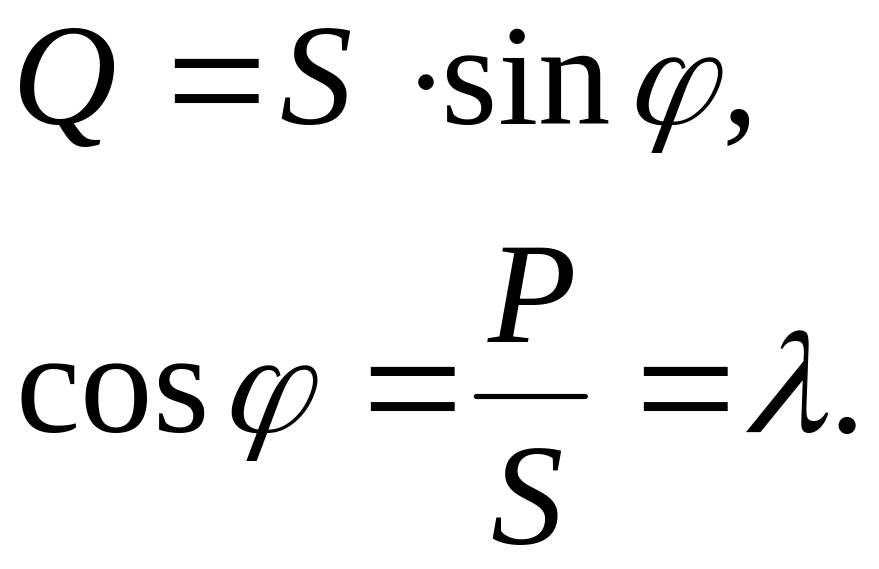(11.26)

Полная мощность S – это теоретически достижимая, расчетная

мощность, По значению S производятся расчеты сечения проводов, изоляция, параметры приемников электрической энергии. Из-за сдвига фаз φ мощность полностью не реализуется. Поэтому cosφ и получил название коэффициента мощности. Значение коэффициента мощности всегда стремятся обеспечить достаточно большим.

3. Выражение мощности в комплексной форме

Широкое применение комплексного представления тока и напряжения в процессе анализа электрических цепей предполагает найти комплексное представление для активной, реактивной и полной мощности. На первый взгляд, эта задача не должна вызывать затруднений. Достаточно в выражение для мощности подставить комплексные значения тока и напряжения. Посмотрим, так ли это?

Пусть заданы комплексные ток и напряжение . Тогда их произведение должно представлять комплексную форму полной мощности цепи:

Правая часть полученного выражения должна определять активную (действительную часть) и реактивную (мнимую часть) мощности. Но слагаемые правой части не соответствуют выражениям (11.15) и (11.21), так как в последних сдвиг фаз определяется разностью

φ = φ₁ – φ₂.

Чтобы устранить такое несоответствие, пользуются искусственным приемом. Под комплексным изображением полной мощности понимают произведение комплексного напряжения на комплексно-сопряженный ток. Напомним, что два комплексных числа и называются взаимно сопря-женными, если их действительные части равны, а мнимые отличаются только

знаком. Например,

При таком определении комплексная мощность цепи определится таким выражением:

Применим действующие значения тока и напряжения. Тогда выражение для комплексной мощности принимает вид:

(11.27)

Знак «тильда» означает комплекс полной мощности, составленный при участии сопряженного комплекса тока. Действительная часть комплексной мощности есть активная мощность, а мнимая часть - реактивная мощность. Модуль комплексного представления определяет полную мощность.

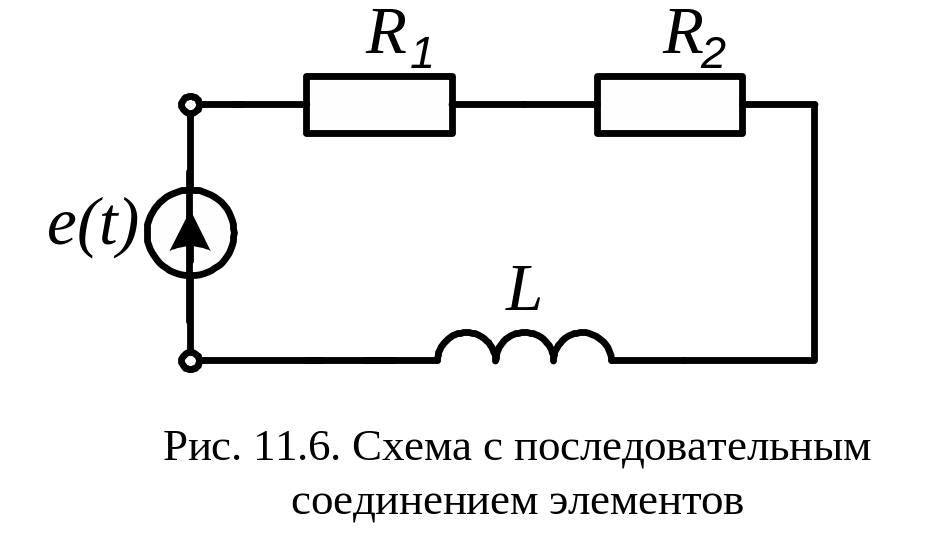
Рассмотрим пример. Пусть в схеме рис. 11.6 заданы Э.Д.С. – e(t) = 141∙sin(ω∙t) [B] и параметры элементов: R₁=3 Ом; R₂=2 Ом; L=0,0095 Гн; .

Определить активную, реактивную и полную мощности цепи.

Решение:

1. Определяем значение действующего напряжения на входе всей схемы в комплексной форме:

2. Определяем сопротивление цепи в комплексной алгебраической форме:

3. Переходим к показательной форме комплексного сопротивления. Для этого:

а) находим модуль

б) фазу

в) общее выражение

4. Вычисляем значение действующего тока в показательной комплексной форме:

Сопряженный комплекс тока:

_.

5. Переходим к определению мощности в комплексной форме:

Отсюда