4.Индуктивность

При изменении тока в контуре или катушке изменяется потокосцепление самоиндукции или собственное потокосцепление, обусловленное током в этом контуре, а также взаимное потокосцепление с другим контуром или катушкой.

Опыт показывает, что одинаковое изменение тока в двух контурах или катушках приводит в общем случае к различному изменению их потокосцепления. Особенности любого контура или катушки в отношении образования потокосцепления определяются их собственной и взаимной индуктивностью.

4.1. Собственная индуктивность

На зависимость между током и потокосцеплением уединенного контура влияют факторы, обусловленные его конструкцией (форма, размеры, среда). Для количественной оценки этого влияния введено понятие индуктивности контура или катушки.

Собственная индуктивность уединенного контура или катушки определяется отношением потокосцепления самоиндукции контура (катушки) к току в нем

[Гн]. (5.15)

В вакууме и неферромагнитных веществах это отношение постоянно, т. е. не зависит от значений тока и потокосцепления.

Наиболее распространенными элементами электротехнических устройств являются контуры, катушки, двухпроводные линии. Определим выражения для оценки их индуктивности.

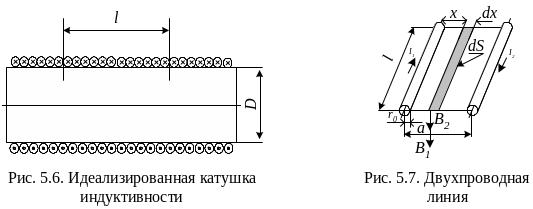
Определим индуктивность участка l бесконечно длинной цилиндрической катушки, имеющей на этом участке витков диаметром D (рис. 5.6).

Магнитное поле такой катушки равномерное, а магнитная индукция определяется выражением (5.7) . Витки катушки плотно прилегают друг к другу, поэтому потокосцепление всех витков можно считать одинаковым и равным

, S= π·D²/4.

В соответствии с формулой (5.15) получаем

. (5.16)

В практике применяются катушки различной формы, без соблюдения условия l_k >> D, поэтому для расчетов используют расчетные кривые, эмпирические формулы, а также поправочные коэффициенты к формуле (5.16), приводимые в справочниках.

Схема участка двухпроводной линии приведена на рис. 5.7. Для определения индуктивности такой линии по (5.15) необходимо предварительно подсчитать потокосцепление. Поток, сцепленный с контуром, образованным прямым и обратным проводами линии, можно подсчитать по (5.9), учитывая, что поле линейного тока неравномерное.

Выделим между проводами элемент площади dS = l·dx, в пределах которой магнитную индукцию можно считать постоянной. Тогда

dФ = В·l·dx

или

.

-

Поток, образованный током прямого провода, определим суммированием элементарных потоков на всем расстоянии между проводами в свету:

.

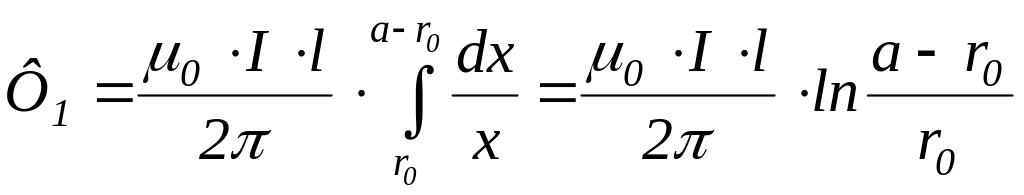Учитывая, что а >> r₀, вместо a – r₀ можно взять а:

.

Такой же поток и в том же направлении создается током обратного провода, поэтому общий поток равен 2Ф₁:

.

Двухпроводная линия образует уединенный контур, поэтому потокосцепление .

Применяя формулу (5.15) определяем индуктивность:

. (5.17)

Формула (5.17) не учитывает внутреннюю индуктивность, образованную магнитным потоком внутри проводов, поэтому может применяться для приближенных расчетов.