Тема III. Магнитные цепи лекция 5. Элементы теории магнитных цепей

Электрический ток, протекающий по проводнику, создает вокруг него магнитное поле. Магнитное поле обнаруживается благодаря магнитным явлениям: притяжению и отталкиванию проводов с токами, намагниченных тел, электромагнитной индукции.

Изучение этих явлений и расчеты, связанные с их использованием, невозможны без количественной оценки магнитного поля. В лекции рассматриваются основные явления, понятия, определения и оценки магнитного поля.

1. Магнитная индукция

Опытом установлено, что на каждый из двух проводов действуют силы, притягивающие провода с одинаковым направлением токов и отталкивающие их если направление токов противоположно (рис. 5.1). Количественная оценка силы взаимодействия определена законом Ампера, согласно которому сила взаимодействия между двумя элементами тока в вакууме пропорциональна произведению элементов тока и обратно пропорциональна квадрату расстояния между ними.

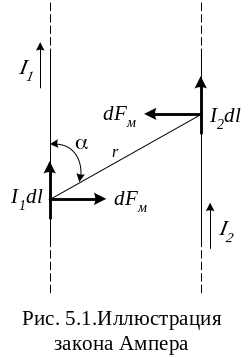
Элементом тока называется произведение I·dl, где dl длина участка провода с током I, пренебрежимо малая по сравнению с расстоянием от него до точек, в которых рассматривается магнитное поле.

Если элементы тока расположены параллельно, то сила взаимодействия между ними определяется выражением

, (5.1)

где r – расстояние между элементами, α – угол между направлением одного из элементов тока и отрезком прямой r, – коэффициент пропорциональности. Числитель этого коэффициента μ₀ называется магнитной постоянной, причем, Гн/м.

Векторная величина, характеризующая магнитное поле и определяющая силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называется магнитной индукцией. В численном выражении магнитная индукция определяется выражением

. (5.2)

Магнитная индукция измеряется в теслах [Тл].

Из формулы (5.1) следует, что элементарная магнитная индукция dB может быть определена выражением

. (5.3)

Выражение (5.3) устанавливает связь тока с его магнитным полем и является математическим выражением закона Био – Савара. Закон Био – Савара применяют для определения основных характеристик магнитного поля в любом случае. Более просто такие задачи решаются на основе понятий о циркуляции векторов магнитной индукции и полном токе.

Рассмотрим понятие о циркуляции по рис. 5.2. В каждой точке произвольного замкнутого контура вектор магнитной индукции В может иметь любое направление. Проекцию этого вектора на направление элемента dl около выбранной точки контура обозначим В_i. Тогда циркуляция вектора магнитной индукции определится выраженим

.

Алгебраическую сумму токов , пронизывающих поверхность, ограниченную контуром, называют полным током.

На основе закона Био – Савара доказано, что

. (5.4)

К огда контур совпадает с линией магнитной индукции вместо проекции вектора B_i в формулу (5.4) можно подставить его полную величину. Тогда

. (5.5)

Графически магнитное поле изображается линиями магнитной индукции. Линию магнитной индукции проводят так, чтобы в каждой ее точке касательная к линии совпадала с вектором магнитной индукции.

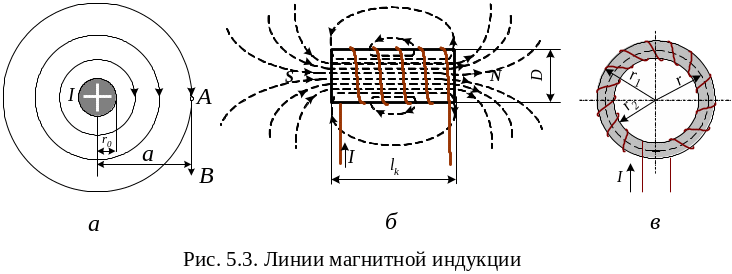
Магнитное поле тока прямолинейного провода имеет линии магнитной индукции в виде окружностей, в плоскостях перпендикулярных направлению тока (рис. 5.3, а). Направление магнитной индукции в этом случае определяется правилом буравчика: если направление поступательного движения буравчика совместить с направлением тока, то вращение рукоятки совпадет с направлением линий магнитной индукции.

Для оценки магнитной индукции на произвольном расстоянии а от оси провода наметим точку А и проведем чрез нее замкнутый контур, совпадающий с линией магнитной индукции. Контур представляет окружность с центром на оси провода, поэтому магнитная индукция во всех точках контура одинакова. Согласно (5.5) можем записать

В· 2·π·а = μ₀·I

Откуда

(5.6)

где 2π·а – длина контура.

Магнитное поле тока цилиндрической катушки показано на рис. 5.3, б. Если длина катушки значительно больше ее диаметра, то величина магнитной индукции внутри катушки во всех точках одинакова, за исключением краевых точек. Такое поле называется равномерным или однородным.

Если полагать, что витки катушки навиты вплотную друг к другу, а ее длина бесконечна, то все точки на любой линии, параллельной оси, находятся в одинаковых условиях. Магнитная индукция поля внутри идеализированной катушки во всех точках одинакова и направлена вдоль оси. Вне катушки магнитного поля нет. Поэтому циркуляция вектора магнитной индукции имеет величину .

Полный ток контура катушки , где – число витков катушки. Согласно выражению (5.5)

. (5.7)

Формулу (5.7) можно применять, допуская некоторую погрешность, если длина реальной катушки значительно больше диаметра l >> D.

Кольцевая катушка с обмоткой на тороидальном сердечнике (рис. 5.3, в) создает магнитное поле только внутри витков.

Выберем замкнутый контур радиусом r, совпадающий с линией магнитной индукции в центре сечения сердечника. Полагая намотку витков равномерной, применим формулу (5.5). Тогда

. (5.8)

Направление линий магнитной индукции катушки или контура определяется тоже правилом буравчика, но в другой формулировке: если рукоятку буравчика вращать по направлению тока в витках, то поступательное движение буравчика совпадает с направлением линий магнитной индукции.