7.1. Замена нескольких параллельных ветвей с источниками

электрической энергии одной эквивалентной

На рис. 2.11, а приведен фрагмент схемы некоторой электрической цепи. Если необходимо определить только ток неразветвленной части цепи I, то это проще сделать по участку цепи, приведенному на рис. 2.11, б. Рассмотрим правила определения Е_э и R_э при которых участки цепи рис. 2.11, а и рис. 2.11, б будут эквивалентны.

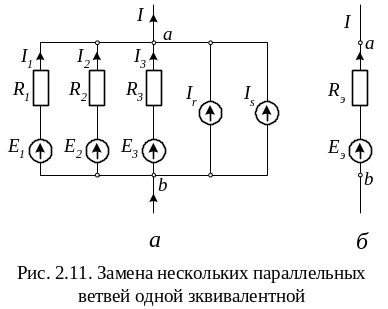
Для схемы рис. 2.11, а справедливо уравнение

I = I₁ + I₂ + I₃ + I_r + I_s.

Выразим токи ветвей с источниками Э.Д.С. по закону Ома:

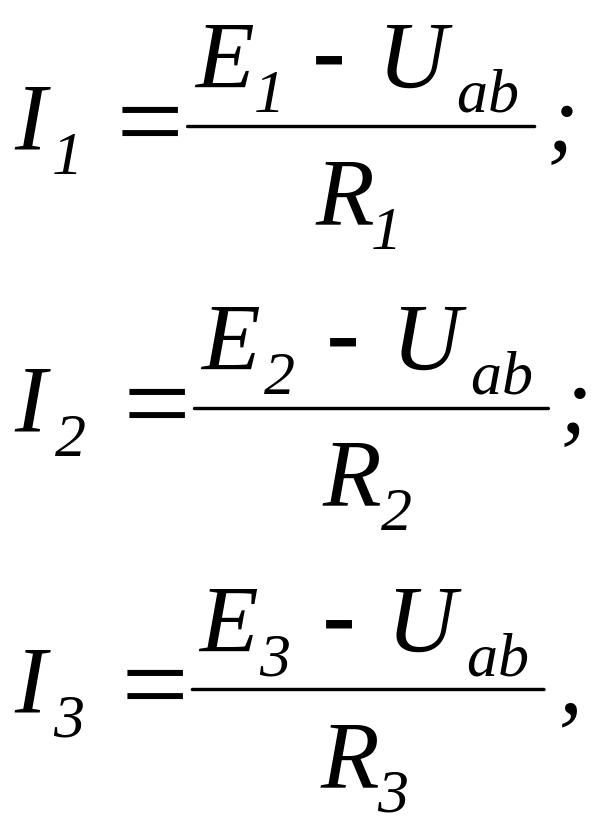(2.14)

где U_ab – напряжение на зажимах a и b.

Следовательно, ток неразветвленной части цепи рис. 2.11, а можно определить уравнением

. (2.15)

В (2.15) n – число ветвей с источниками Э.Д.С., q – число ветвей с источниками тока.

Ток схемы рис. 2.11, б определим по закону Ома

. (2.16)

Если схемы рис. 2.11, а и б эквивалентны, то их токи I и напряжения U_ab равны. Приравняем правые части (2.15) и (2.16) и перейдем от сопротивлений к проводимостям. Тогда

Следовательно

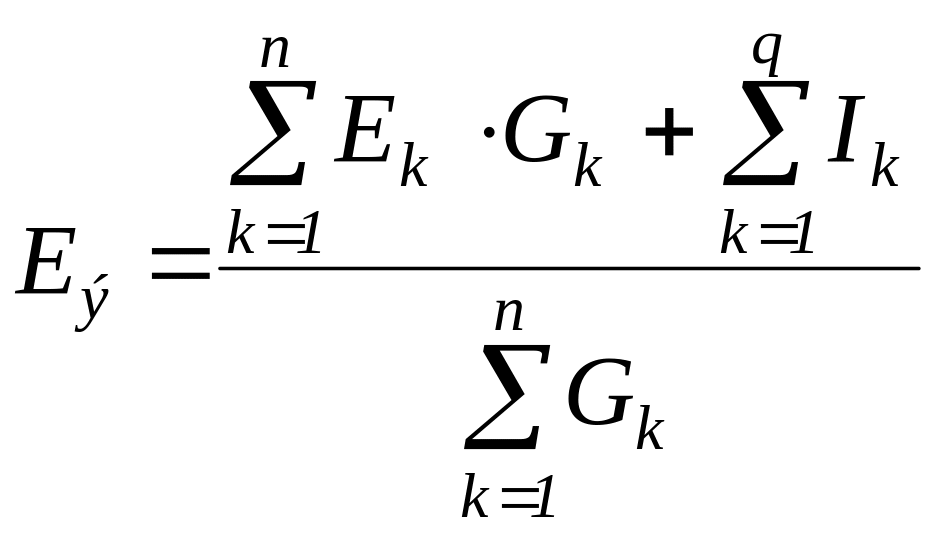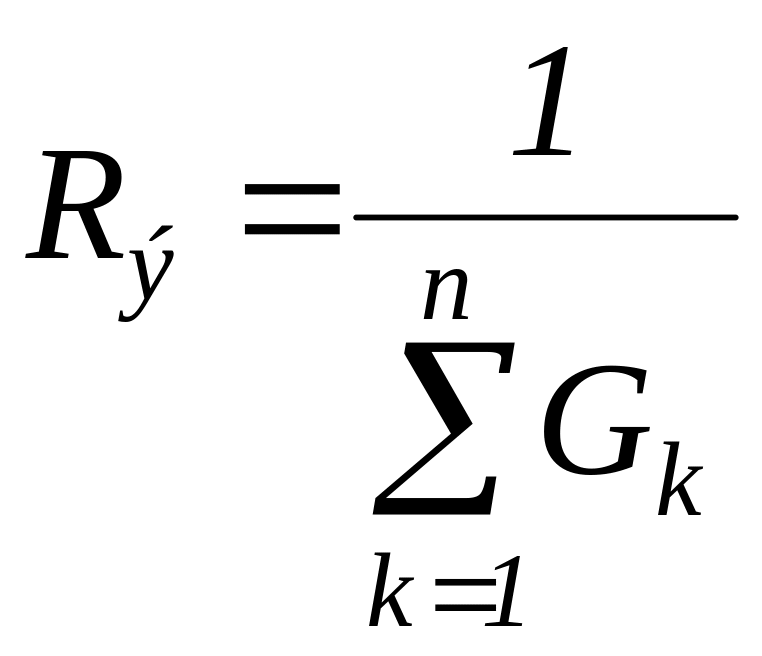, . (2.17)

7.2. Метод двух узлов

Метод рационален для анализа схем, содержащих только два сложных потенциальных узла. Схема рис. 2.12 отличается от схемы рис. 2.11, а только тем, что в ней нет неразветвленной части, т. е. ток I = 0. В методе двух узлов за искомое принимают напряжение между сложными потенциальными узлами схемы. Тогда определение токов в ветвях цепи сводится к применению закона Ома.

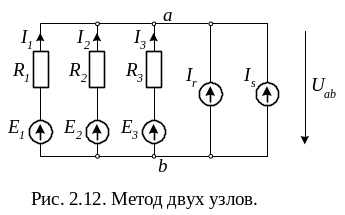
Так как в схеме рис. 2.12 ток I = 0, то из выражения (2.15) легко найти U_ab:

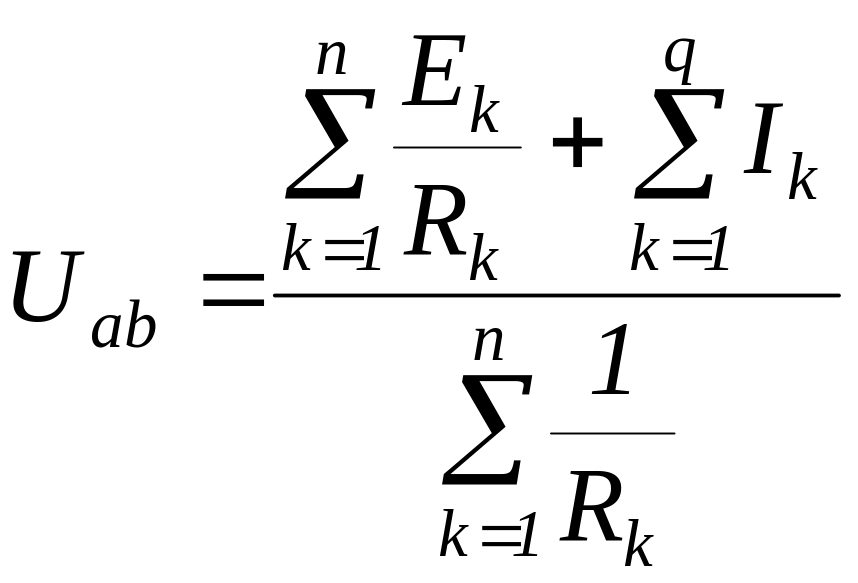. (2.18)

После определения напряжения U_ab находят токи любой ветви по формуле (2.14).

Примечание:

при расчетах по формулам (2.17) и (2.18) следует учитывать, что если в какой-либо ветви схемы Э.Д.С. отсутствует, то соответствующие слагаемые в числителях (2.17) и (2.18) выпадают, но проводимости ветвей в знаменателях формул остаются;

в выражениях (2.17) и (2.18) слагаемые и I_k берут со знаком плюс, когда направления Е_k и I_k противоположны выбранному условно – положительному направлению напряжения U_ab, и со знаком минус, когда эти направления совпадают.

7.3. Метод узловых потенциалов

Метод узловых потенциалов, как и метод контурных токов , – один из основных расчетных приемов. Когда число сложных потенциальных узлов без единицы меньше числа независимых контуров в схеме, данный метод более экономичен, чем метод контурных токов.

Суть метода заключается в применении закона Ома к участку цепи с Э.Д.С. или без нее. Чтобы применить закон Ома, необходимо знать потенциалы узлов схемы. Поэтому в методе узловых потенциалов за неизвестные принимают потенциалы узлов схемы.

Рассмотрим применение метода на примере схемы, приведенной на рис. 2.13. В схеме четыре сложных потенциальных узла (четвертый узел заземлен, его потенциал φ₄ = 0) и четыре независимых контура. К анализу такой схемы можно применить метод контурных токов (относительно четырех неизвестных контурных токов) или метод узловых потенциалов (относительно трех неизвестных потенциалов узлов φ₁, φ₂ и φ₃). Очевидно, что метод узловых потенциалов более предпочтителен.

Введем обозначения, понятия и определения, которыми необходимо пользоваться в процессе анализа методом узловых потенциалов.

Искомые потенциалы узлов обозначим φ₁, φ₂ и φ₃.

Сумму проводимостей всех ветвей, сходящихся в каждом из сложных потенциальных узлов, условно назовем узловой проводимостью. Узловую проводимость будем обозначать двумя индексами, например G₁₁, G₂₂, G₃₃. Например,

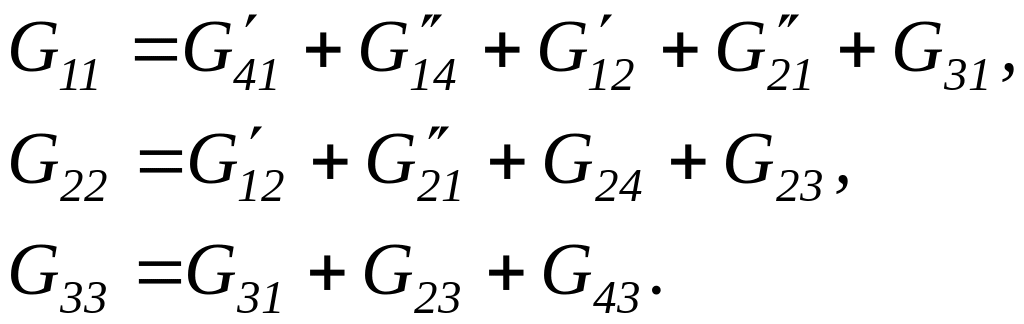(2.19)

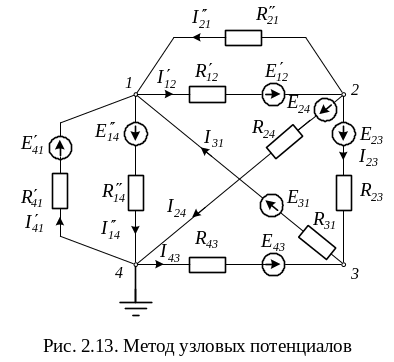
Сумму проводимостей всех ветвей соединяющих два узла, взятую со знаком минус, условно назовем междуузловой проводимостью. Междуузловую проводимость также будем обозначать двумя индексами, например G₁₂, G₂₃, G₃₁. Например,

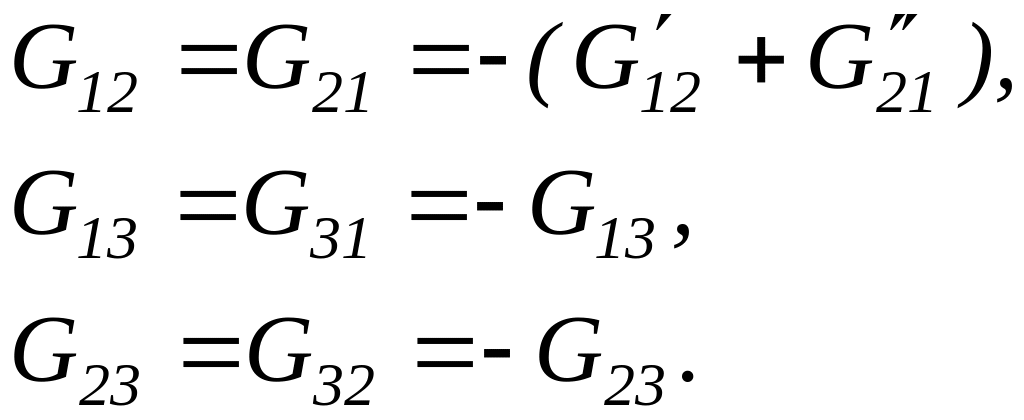(2.20)

Алгебраическую сумму токов, равную частному от деления Э.Д.С. ветвей, подходящих к рассматриваемому узлу, на сопротивления данных ветвей условно назовем узловым током. В сумму со знаком плюс входят токи тех ветвей, Э.Д.С. которых направлены к рассматриваемому узлу. Это расчетная величина, обозначаемая двумя индексами по номеру узла – I₁₁, I₂₂, I₃₃. Для схемы рис. 2.13

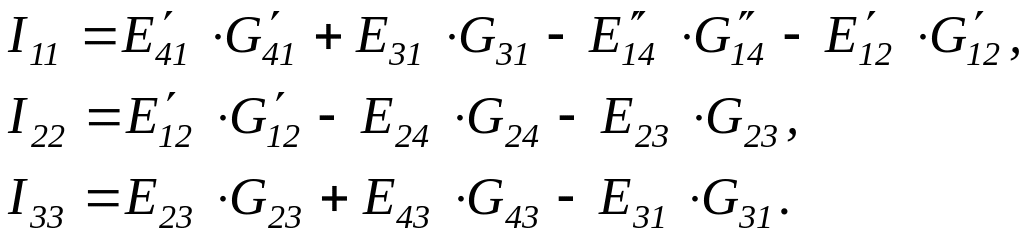(2.21)

Введенные в (2.19), (2.20) и (2.21) величины позволяют записать для каждого узла уравнение по первому закону Кирхгофа в канонической форме

(2.22)

Если в k-узел втекает ток от источника тока, то он должен быть включен в ток I_kk со знаком плюс, если вытекает, то со знаком минус.

После решения системы (2.22) относительно потенциалов определяют токи в ветвях по закону Ома для участка цепи, содержащего Э.Д.С.

Для примера найдем токи в ветвях схемы рис.2.13 при следующих значениях параметров элементов:

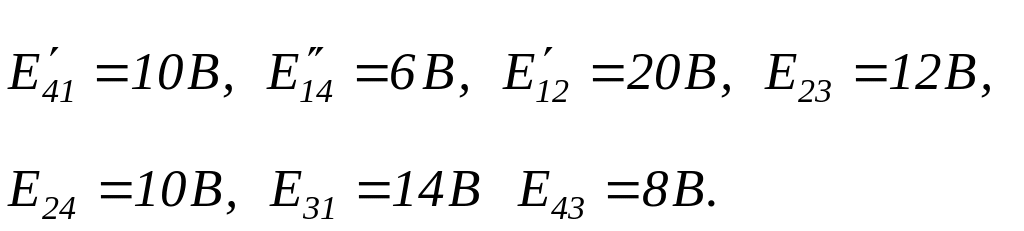
Для решения задачи применяем метод узловых потенциалов. Исходная система уравнений имеет вид (2.22). Узловые проводимости определяем по (2.19):

Аналогично находим G₂₂ = 0,7 См, G₃₃ = 1,25 См.

Междуузловые проводимости рассчитываем по (2.20):

G₁₂ = G₂₁ = -0,2 См,

G₁₃ = G₃₁ = -0,5 См,

G₂₃ = G₃₂ = -0,25 См.

Узловые токи находим по (2.21): I₁₁ = 12A, I₂₂ = -3,5A, I₃₃ = 0.

Система уравнений

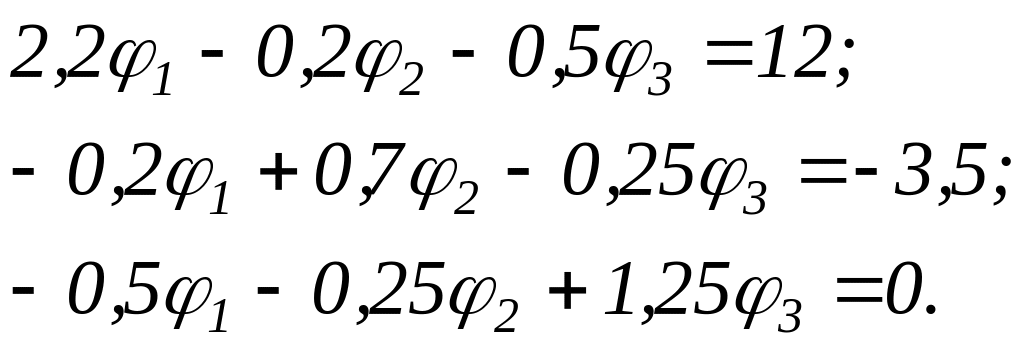
имеет решение: φ₁ = 9,243 В, φ₂ = 3,076 В, φ₃ = 15,4 В.

Определяем токи ветвей по закону Ома. Будем полагать, что условно выбранные положительные направления токов показаны на схеме стрелками. Тогда:

и т. д.

Проверку решения выполним по второму закону Кирхгофа для периферийного контура. При обходе контура по часовой стрелке, с учетом знаков и условно выбранных положительных направлений токов алгебраическая сумма падений напряжений равна

1·0,757 – 10·(-0,616) + 4·(-0,081) - 2·(-3,7) =13,993В.

́Алгебраическая сумма Э.Д.С. равна 10 + 12 – 8 = 14В.