5. Метод наложения

Принцип наложения формулируется следующим образом: ток в к-ветви равен алгебраической сумме токов, вызываемых каждой из Э.Д.С. схемы в отдельности. Принцип наложения используется при анализе электрических цепей и получил название метода наложения.

При анализе по методу наложения поочередно рассчитывают частичные токи, возникающие от действия отдельно взятой Э.Д.С. схемы. При этом полагают, что остальные Э.Д.С. удалены из схемы, но оставлены их внутренние сопротивления. Реальные токи ветвей находят алгебраическим сложением частичных токов.

Рассмотрим применение метода на примере анализа схемы по рис. 2.8, а. Необходимо найти токи в ветвях, а также мощности, доставляемые источником тока и источником Э.Д.С., полагая R₁ = 2 Ом, R₂ = 4 Ом, R₃ = 6 Ом, I_k = 5 А, Е = 20 В.

Положительные направления токов принимаем по рис. 2.8, а. С помощью схемы рис.2.8, б (в ней исключен источник Э.Д.С., а зажимы сd закорочены) находим частичные токи в ветвях от действия источника тока I_k:

; ; .

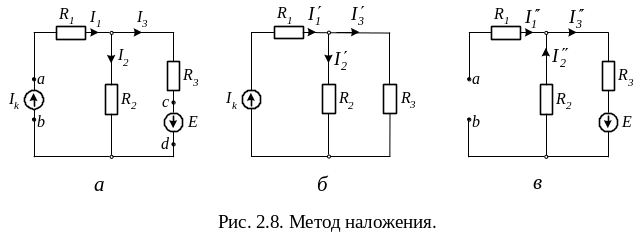
Используя схему рис.2.8, в, определяем частичные токи в ветвях от действия источника Э.Д.С. (Зажимы аb разомкнуты, так как внутреннее сопротивление источника тока равно бесконечности):

; .

Результирующие токи находим алгебраической суммой частичных токов:

; ;

; .

Мощность, доставляемая в схему источником тока, определяется произведением .

Мощность, доставляемая в схему источником Э.Д.С. .

6. Полезные для практики понятия и определения

6.1.Входные и взаимные проводимости ветвей

Рассмотрим понятия по скелетной схеме пассивной цепи, приведенной на рис. 2.9, а. На схеме показаны только ветви и узлы. В каждой ветви имеется сопротивление. Выделим в схеме две ветви: одну из них обозначим ветвью m, другую – ветвью k.

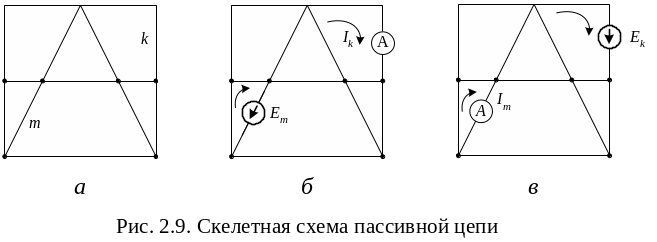
Изменим схему: в ветвь m включим источник Э.Д.С., а в ветвь k – амперметр, как на рис. 2.9, б. Выберем контуры в схеме так, чтобы k-ветвь входила только в k-контур, а m-ветвь – только в m-контур. Тогда Э.Д.С. Е_m вызовет в ветвях k и m следующие токи

(2.13)

В (2.13) коэффициент G_mm называют входной проводимостью ветви m. Это коэффициент пропорциональности между током и Э.Д.С. одной и той же ветви. Коэффициент G_km называют взаимной проводимостью k-й и m-й ветвей. Это коэффициент пропорциональности между током k-ветви и Э.Д.С. m-ветви.

6.2. Теорема взаимности

Формулировка теоремы: для любой линейной цепи ток в k-ветви, вызванный Э.Д.С. Е_m, находящейся в m-ветви

будет равен току I_m в m-ветви, вызванному Э.Д.С. Е_k, находящейся в k-ветви

.

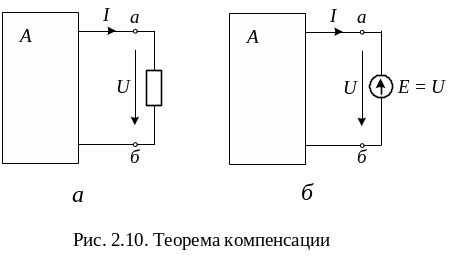
6.3. Теорема компенсации

Формулировка теоремы: в любой электрической цепи без изменения токораспределения в ней сопротивление можно заменить Э.Д.С., численно равной падению напряжения на заменяемом сопротивлении и направленной встречно току в этом сопротивлении.

7. Методы анализа электрических цепей

ПРИМЕНЕНИЕМ ЗАКОНА ОМА

В реальных электрических цепях достаточно часто встречаются фрагменты с параллельным соединением нескольких ветвей содержащих Э.Д.С. Такие фрагменты или схемы в целом имеют только два узла. Если напряжение между узлами (разность потенциалов) известно, то определение токов в ветвях цепи сводится к применению закона Ома. Этот факт и положен в основу ряда методов анализа.